Toptailieu.vn giới thiệu Giải bài tập Toán 9 Bài 6: Tính chất của hai tiếp tuyến cắt nhau chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Căn bậc hai lớp 9.
Giải bài tập Toán 9 Bài 6: Tính chất của hai tiếp tuyến cắt nhau
Trả lời câu hỏi giữa bài:
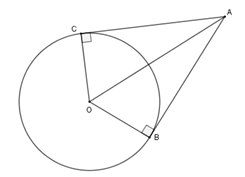
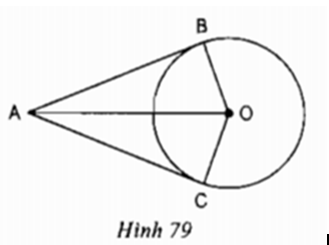
Trả lời câu hỏi 1 trang 113 SGK Toán 9 Tập 1: Cho hình 79 trong đó AB, AC theo thứ tự là các tiếp tuyến tại B, tại C của đường tròn (O). Hãy kể tên một vài đoạn thẳng bằng nhau, một vài góc bằng nhau trong hình.
Phương pháp giải:
Sử dụng tính chất hai tam giác bằng nhau
Lời giải:
Xét đường tròn (O) có AB và AC là hai tiếp tuyến lần lượt tại B và C nên
Xét hai tam giác vuông là và có:
+ AO cạnh chung
+ OB=OC =bán kính
Suy ra (cạnh huyền - cạnh góc vuông)
Từ đó ta có:
Các đoạn thẳng bằng nhau là: AB = AC ; OB = OC
Các góc bằng nhau là:
Trả lời câu hỏi 2 trang 114 SGK Toán 9 Tập 1: Hãy nêu cách tìm tâm của một miếng gỗ hình tròn bằng “thước phân giác” (xem hình vẽ trong khung ở đầu bài 6).
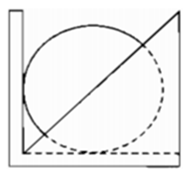
Lời giải:
- Ta đặt miếng gỗ hình tròn tiếp xúc với hai cạnh của thước.
- Kẻ theo “ tia phân giác “ của thước, ta vẽ được một đường kính của hình tròn
- Xoay miếng gỗ rồi làm tiếp tục như trên, ta được đường kính thứ hai.
- Giao điểm của hai đường kính chính là tâm đường tròn
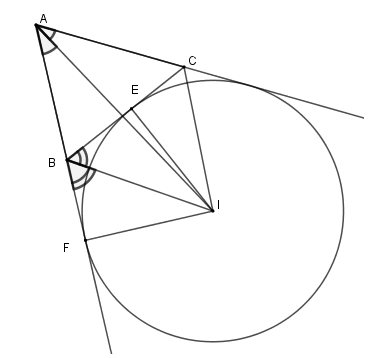
Trả lời câu hỏi 3 trang 114 SGK Toán 9 Tập 1: Cho tam giác ABC. Gọi I là giao điểm của các đường phân giác các góc trong của tam giác; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ I đến các cạnh BC, AC, AB (h.80). Chứng minh rằng ba điểm D, E, F nằm trên cùng một đường tròn tâm I.
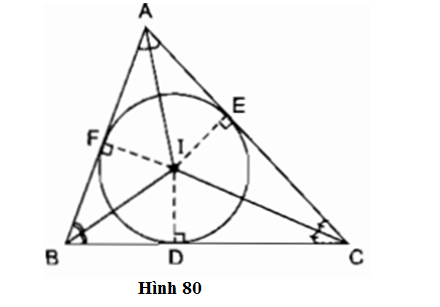
Phương pháp giải:
Sử dụng: Các điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Lời giải:
Xét tam giác ABC. Theo tính chất tia phân giác, ta có:
AI là tia phân giác của góc BAC
Tương tự: CI là tia phân giác của góc ACB
Do đó:
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm I.
Trả lời câu hỏi 4 trang 115 SGK Toán 9 Tập 1: Cho tam giác ABC, K là giao điểm các đường phân giác của hai góc ngoài tại B và C; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ K đến các đường thẳng BC, AC, AB (h.81). Chứng minh rằng ba điểm D, E, F năm trên cùng một đường tròn có tâm K.
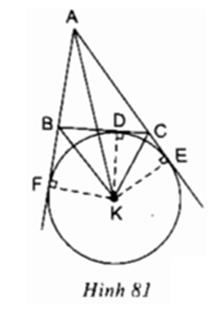
Phương pháp giải:
Sử dụng tính chất tia phân giác: "Các điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó"
Lời giải:
Theo tính chất tia phân giác, ta có:
AK là tia phân giác của góc BAC
Tương tự: CK là tia phân giác của góc ngoài của góc ACB
Do đó: KE = KF = KD
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm K
Bài tập trang 115-116 SGK Toán 9
Bài 26 trang 115 SGK Toán 9 tập 1: Cho đường tròn , điểm nằm bên ngoài đường tròn. Kẻ các tiếp tuyến với đường tròn ( là các tiếp điểm).
a) Chứng minh rằng vuông góc với .
b) Vẽ đường kính . Chứng minh rằng song song với .
c) Tính độ dài các cạnh của tam giác ; biết .
Phương pháp giải:
a) Tính chất hai tiếp tuyến cắt nhau: cho với hai tiếp tuyến . Khi đó:
+)
+) là phân giác của góc
b) Sử dụng tính chất: nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp tam giác thì tam giác đó là tam giác vuông (Bài tập 3 - trang 100)
c) +) Dùng định nghĩa tỉ số lượng giác trong tam giác vuông: để tính số đo góc.
+) Tam giác cân có một góc bằng thì là tam giác đều.
+) Dùng định lí Pytago: vuông tại thì .
Lời giải:
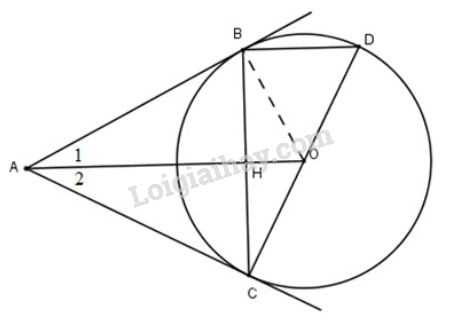
a) Vì là các tiếp tuyến cắt nhau tại A nên và (tính chất hai tiếp tuyến cắt nhau)
Suy ra cân tại .
Vì nên là tia phân giác của góc nên đồng thời là đường cao ứng với cạnh .
Vậy
b) Điểm nằm trên đường tròn đường kính nên (bài 3 trang 100 SGK toán 9 tập 1) hay .
Lại có
Suy ra (vì cùng vuông góc với .
c) Nối thì
Xét tam giác vuông tại , ta có:
Tam giác cân, có một góc nên là tam giác đều.
Suy ra
Xét tam giác vuông tại , áp dụng định lí Pytago, ta có:
Vậy .
Nhận xét. Qua câu c) ta thấy: Góc tạo bởi hai tiếp tuyến của một đường tròn vẽ từ một điểm cách tâm một khoảng bằng đường kính đúng bằng .
Cách khác câu b:
Gọi H là giao điểm của OA và BC.
Vì tại H mà OA là 1 phần đường kính và BC là dây của đường tròn (O) nên H là trung điểm của BC (định lý)
Lại có O là trung điểm của đường kính CD nên OH là đường trung bình của tam giác BCD
Hay OH//BD. Do đó, OA//BD.
Bài 27 trang 115 SGK Toán 9 tập 1: Từ một điểm nằm bên ngoài đường tròn , kẻ các tiếp tuyến với đường tròn ( là các tiếp điểm). Qua điểm thuộc cung nhỏ , kẻ tiếp tuyến với đường tròn , nó cắt các tiếp tuyến và theo thứ tự ở và . Chứng minh rằng chu vi tam giác bằng .
Phương pháp giải:
+) Sử dụng tính chất hai tiếp tuyến cắt nhau: cho với hai tiếp tuyến tại của khi đó .
+) Chu vi tam giác là: .
Lời giải:
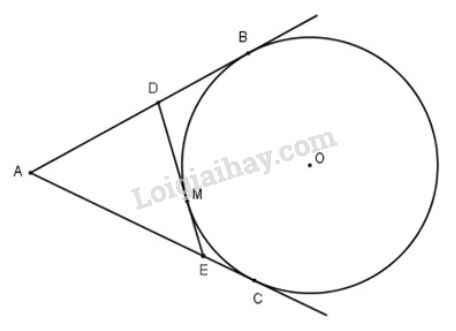
Vì là hai tiếp tuyến của lần lượt tại . Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
Vì là hai tiếp tuyến của lần lượt tại . Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
Vì là hai tiếp tuyến của lần lượt tại . Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
Chu vi tam giác là:
(vì và )
(vì ).
Bài 28 trang 116 sgk Toán 9 - tập 1: Cho góc khác góc bẹt. Tâm của các đường tròn tiếp xúc với hai cạnh của góc nằm trên đường nào?
Phương pháp giải:
Sử dụng tính chất của hai tiếp tuyến cắt nhau: Cho với hai tiếp tuyến . Khi đó: là phân giác của góc
Lời giải:
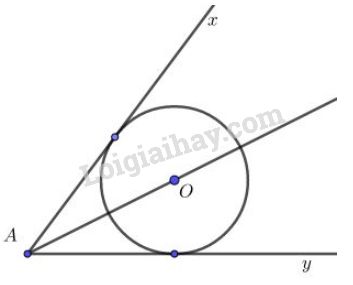
Gọi là tâm của một đường tròn bất kì tiếp xúc với hai cạnh góc . Khi đó là hai tiếp tuyến của đường tròn . Theo tính chất của hai tiếp tuyến cắt nhau ta có:
Hay là tia phân giác của góc . Vậy tập hợp tâm các đường tròn tiếp xúc với hai cạnh của góc nằm trên tia phân giác của góc .
Bài 29 trang 116 sgk Toán 9 - tập 1: Cho góc khác góc bẹt, điểm thuộc . Hãy dựng đường tròn tiếp xúc với tại và tiếp xúc với .
Phương pháp giải:
Bài toán dựng hình chia làm bước:
Bước 1. Phân tích: giả sử hình cần dựng đã được vẽ. Lập luận để tìm cách dựng được hình.
Bước 2. Dựng hình: Dựa vào bước phân tích trên liệt kê thứ tự các phép dựng hình cơ bản.
Bước 3. Chứng minh: Bằng lí luận, chứng minh hình vừa dựng thỏa mãn tất cả các giả thiết của bài toán.
Bước 4. Biện luận: thiết lập điều kiện giải được của bài toán. Tức là xét xem bài toán giải được trong trường hợp nào và có bao nhiêu nghiệm.
Lời giải:
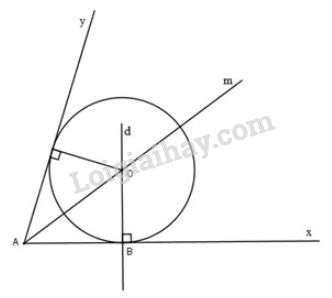
Phân tích: Giả sử đã dựng được hình thỏa mãn đề bài. Khi đó:
Đường tròn tiếp xúc với hai cạnh của góc nên tâm nằm trên tia phân giác của góc (xem lại bài 28 trang 116 SGK toán 9 tập 1).
Đường tròn tiếp xúc với tại nên tâm nằm trên đường thẳng tại .
Vậy là giao điểm của tia với đường thẳng .
Cách dựng
- Dựng tia phân giác Am của góc .
- Qua dựng đường thẳng , cắt tia tại .
- Dựng đường tròn , đó là đường tròn phải dựng.
Chứng minh
Vì tại nên đường tròn tiếp xúc với tại .
Vì nằm trên tia phân giác của góc nên cách đều hai cạnh của góc . Do đó đường tròn tiếp xúc với .
Biện luận. Bài toán luôn có một nghiệm hình.
Bài 30 trang 116 sgk Toán 9 - tập 1: Cho nửa đường tròn tâm có đường kính (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi là các tia vuông góc với ( và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ ). Qua điểm thuộc nửa đường tròn ( khác và ), kẻ tiếp tuyến với nửa đường tròn, nó cắt và theo thứ tự ở và .
Chứng minh rằng:
a)
b)
c) Tích không đổi khi điểm di chuyển trên nửa đường tròn.
Phương pháp giải:
+) Sử dụng tính chất hai đường tiếp tuyến cắt nhau: là tiếp tuyến của tại thì
1) ;
2) là tia phân giác của góc .
+) Sử dụng hệ thức lượng trong tam giác vuông: vuông tại , đường cao . Khi đó
Lời giải:
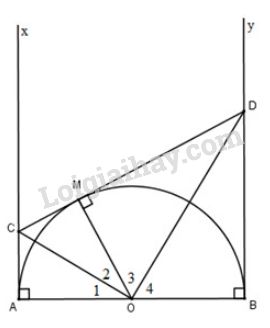
Ta có:
(gt)
(gt)
là các tiếp tuyến của đường tròn lần lượt tại .
Vì là hai tiếp tuyến của lần lượt tại và , theo tính chất hai tiếp tuyến cắt nhau, ta có: và
Vì là hai tiếp tuyến của lần lượt tại và , theo tính chất hai tiếp tuyến cắt nhau, ta có: và
a) Ta có:
b) Ta có: (chứng minh trên)
Lại có: (đpcm)
c) Ta có: (chứng minh trên)
Xét tam giác vuông tại , áp dụng hệ thức lượng trong tam giác vuông, ta có:
Vì bán kính đường tròn không đổi khi di chuyển trên nửa đường tròn nên không đổi do đó tích không đổi khi di chuyển trên nửa đường tròn.
Bài 31 trang 116 sgk Toán 9 - tập 1: Trên hình 82, tam giác ABC ngoại tiếp đường tròn (O).
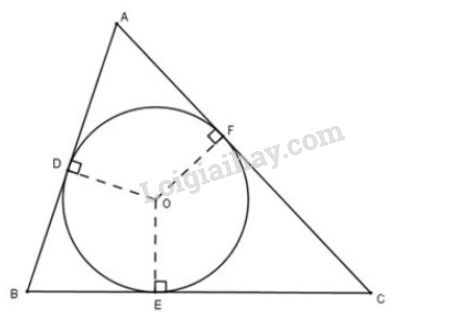
a) Chứng minh rằng:
2AD=AB+AC−BC.
b) Tìm các hệ thức tương tự hệ thức ở câu a).
Phương pháp giải:
+) Sử dụng tính chất hai tiếp tuyến cắt nhau để chứng minh các đoạn thẳng bằng nhau: Nếu là hai tiếp tuyến của lần lượt tại thì ta có:
+) Chu vi tam giác là
Lời giải:
a) Tam giác ngoại tiếp đường tròn tâm nên lần lượt là tiếp tuyến tại của đường tròn.
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
Xét vế phải:
Thay vào biểu thức trên, ta được:
(Do
Vậy
b) Các hệ thức tương tự là:
Nhận xét.
Đặt là nửa chu vi của tam giác , .
Ta có:
hay .
Tương tự ta có các kết quả sau:
Bài 32 trang 116 sgk Toán 9 - tập 1: Cho tam giác đều ngoại tiếp đường tròn bán kính . Diện tích của tam giác bằng:
(A) ;
(B) ;
(C)
(D)
Hãy chọn câu trả lời đúng.
Phương pháp giải:
+) Sử dụng tính chất: Trong tam giác đều, đường cao đồng thời là đường trung tuyến.
+) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông: vuông tại . Khi đó: .
+) Công thức tính diện tích tam giác:
trong đó là độ dài đường cao, là độ dài cạnh ứng với đường cao.
Lời giải:
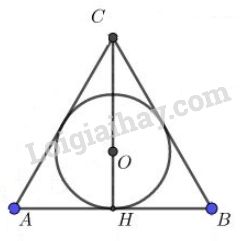
Gọi là đường tròn nội tiếp tam giác đều và H là tiếp điểm thuộc AB.
Khi đó là bán kính của
Ta có:
Trong tam giác đều ABC, đường cao CH cũng là đường trung tuyến.
Vì tam giác ABC đều nên O cũng là trọng tâm tam giác.
Theo tính chất đường trung tuyến, ta có:
Vì tam giác đều nên .
Xét tam giác , vuông tại , . Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông, ta có:
Suy ra
Do đó diện tích tam giác là
Ta chọn (D).
Lý thuyết Bài 6: Tính chất của hai tiếp tuyến cắt nhau
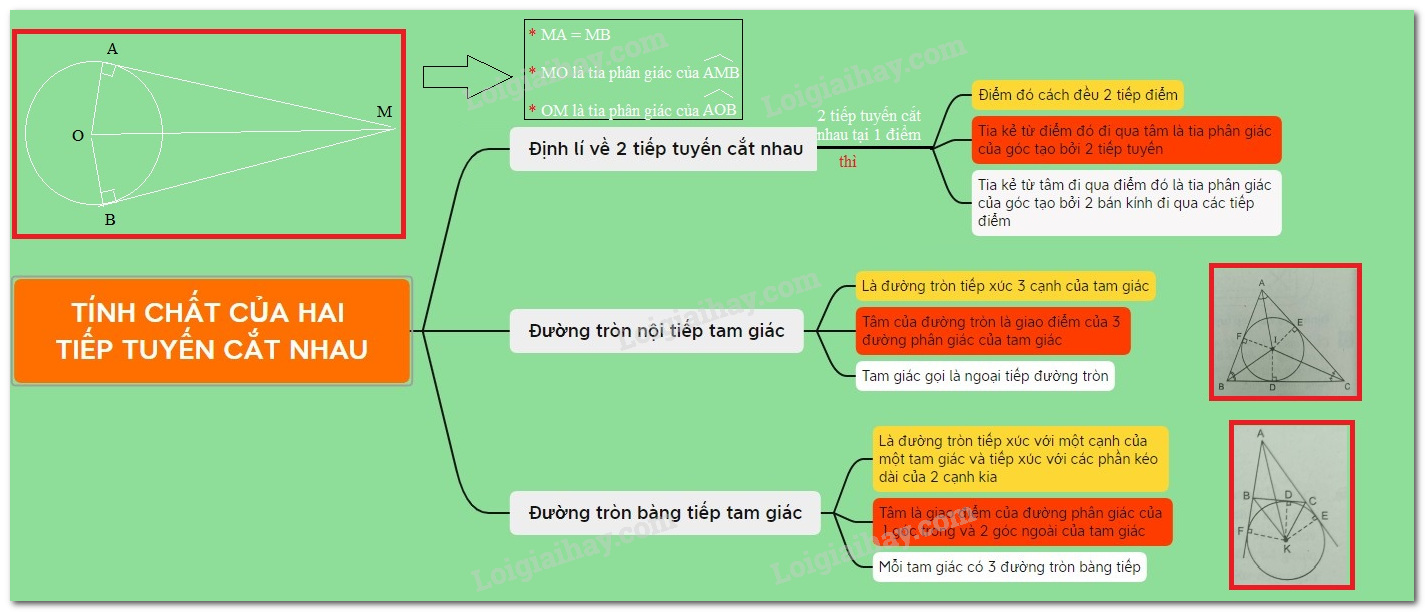
1. Tính chất hai tiếp tuyến cắt nhau
Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:
- Điểm đó cách đều hai tiếp điểm.
- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của các góc tạo bởi hai tiếp tuyến.
- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.
Nghĩa là cho đường tròn , . Tiếp tuyến của tại cắt nhau tại .
Khi đó
-
- Tia là phân giác góc
- Tia là phân giác góc
2. Đường tròn nội tiếp tam giác
Đường tròn tiếp xúc với ba cạnh của một tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn.
Tâm của đường tròn nội tiếp tam giác là giao của các đường phân giác các góc trong tam giác.
3. Đường tròn bàng tiếp tam giác
- Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với phần kéo dài của hai cạnh còn lại gọi là đường tròn bàng tiếp tam giác.
- Tâm của đường tròn bàng tiếp tam giác là giao điểm của 1 đường phân giác trong và 2 đường phân giác ngoài của tam giác
- Với một tam giác có ba đường tròn bàng tiếp.
Ví dụ: Xét tam giác , tâm của đường tròn bàng tiếp tam giác góc $A$ là giao điểm của hai đường phân giác ngoài tại , hoặc là giao điểm của đường phân giác trong góc và đường phân giác ngoài tại (hoặc ).
CÁC DẠNG TOÁN THƯỜNG GẶP
Dạng 1: Chứng minh các đường thẳng song song (vuông góc), chứng minh hai đoạn thẳng bằng nhau.
Phương pháp:
Dùng tính chất của hai tiếp tuyến cắt nhau.
Dạng 2: Chứng minh một đường thẳng là tiếp tuyến, tính độ dài, số đo góc và các yếu tố khác.
Phương pháp:
- Dùng định nghĩa tiếp tuyến; tính chất của hai tiếp tuyến cắt nhau.
- Dùng khái niệm đường tròn nội tiếp, bàng tiếp.
- Dùng hệ thức lượng về cạnh và góc trong tam giác vuông.