Lời giải:
Xét (O) có OM là 1 phần đường kính đi qua trung điểm M của dây AB
(định lý)
Áp dụng định lí Pytago vào tam giác vuông OAM có:
Bài tập trang 104 SGK Toán 9
Bài 10 trang 104 SGK Toán 9 tập 1: Cho tam giác , các đường cao và . Chứng minh rằng:
a) Bốn điểm cùng thuộc một đường tròn.
b)
Phương pháp giải:
a) Sử dụng tính chất: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh đó để chứng minh ba đỉnh của tam giác vuông nằm trên đường tròn đường kính là cạnh huyền.
b) Sử dụng định lí: Trong các dây của đường tròn, dây lớn nhất là đường kính.
Lời giải:
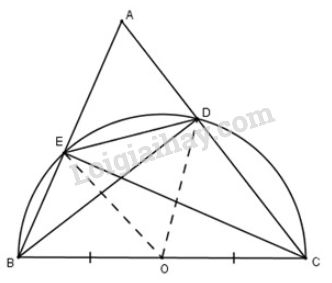
a) Gọi là trung điểm của (1)
Xét tam giác vuông có: (2) (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Xét tam giác vuông có (3) (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Từ (1),(2),(3)
Do đó 4 điểm cùng thuộc đường tròn đường kính .
b) Xét , với là đường kính.
Ta có là một dây không đi qua tâm nên ta có ( vì trong một đường tròn, đường kính là dây lớn nhất).
Bài 11 trang 104 SGK Toán 9 tập 1: Cho đường tròn đường kính , dây không cắt đường kính . Gọi và theo thứ tự là chân các đường vuông góc kẻ từ và đến . Chứng minh rằng
Gợi ý: Kẻ vuông góc với .
Phương pháp giải:
+) Kẻ đường kính vuông góc với dây.
+) Sử dụng tính chất: trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây.
+) Trong hình thang, đường thẳng song song với hai đáy và đi qua trung điểm của một cạnh bên thì đi qua trung điểm của cạnh bên còn lại.
Lời giải:
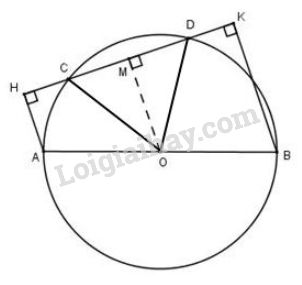
Vẽ
Vì OM là một phần đường kính và CD là dây của đường tròn nên ta có M là trung điểm CD hay (1) (định lý)
Tứ giác có .
Suy ra tứ giác là hình thang.
Xét hình thang , ta có:
(cùng vuông góc với )
mà
là đường trung bình của hình thang .
(2)
Từ (1) và (2) (đpcm)
Nhận xét: Kết quả của bài toán trên không thay đổi nếu ta đổi chỗ hai điểm và cho nhau.
Lý thuyết Bài 2: Đường kính và dây của đường tròn
1. So sánh độ dài của đường kính và dây.
Định lý:
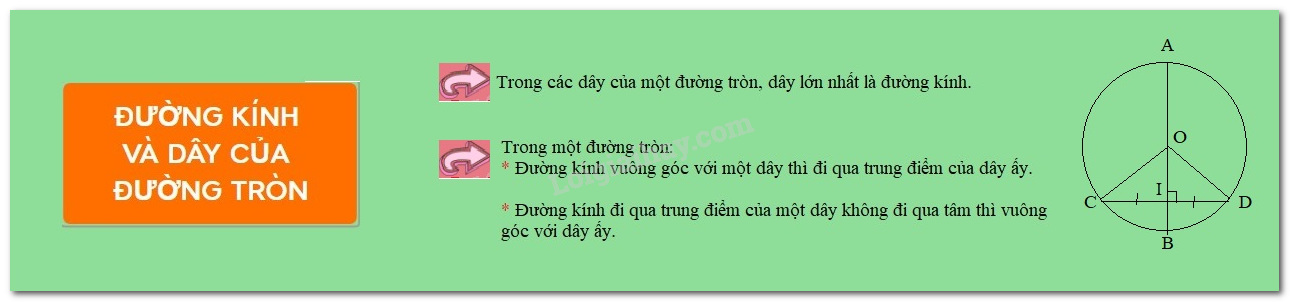
Trong các dây của một đường tròn, dây lớn nhất là đường kính.
Xét đường tròn
2. Quan hệ vuông góc giữa đường kính và dây.
Định lý 1:
- Trong một đường tròn, đường kính vuông góc với một dây thì qua trung điểm của dây ấy.

Xét :
là đường kính
là dây cung
tại
là trung điểm của
Định lý 2:Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.

Xét :
là đường kính
là dây cung,
là trung điểm của ,
tại
3. Các dạng toán thường gặp
Tính độ dài đoạn thẳng và các yếu tố liên quan.
Phương pháp:
Ta thường sử dụng các kiến thức sau:
+) Quan hệ vuông góc giữa đường kính và dây
Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
+) Dùng định lý Pytago, hệ thức lượng trong tam giác vuông.