Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Ôn tập chương 2 - Đường tròn trang 138,139,140,141,142 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:
VBT Toán lớp 9 Ôn tập chương 2 - Đường tròn
Bài 36 trang 138 Vở bài tập toán 9 tập 1
Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H. Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.
a) Hãy xác định vị trí tương đối của các đường tròn: (I) và (O), (K) và (O), (I) và (K).
b) Tứ giác AEHF là hình gì ? vì sao ?
c) Chứng minh đẳng thức AE.AB = AF.AC
d) Dây AD vuông góc với BC tại vị trí nào thì EF có độ dài lớn nhất ?
Phương pháp giải:
a) Xét khoảng cách giữa hai tâm và tổng hoặc hiệu hai bán kính rồi xác định vị trí tương đối của hai đường tròn.
b) Chứng minh tứ giác có ba góc vuông dựa vào kiến thức : “Tiếp tuyến của đường tròn vuông góc với bán kính tại tiếp điểm.
c) Dùng hệ thức lượng về chiều cao và độ dài hình chiếu của các cạnh góc vuông lên cạnh huyền :
d) Ta cần chứng minh và
e) Biểu diễn độ dài theo độ dài của rồi biện luận để tìm vị trí của dây đó vuông góc với .
Trả lời:
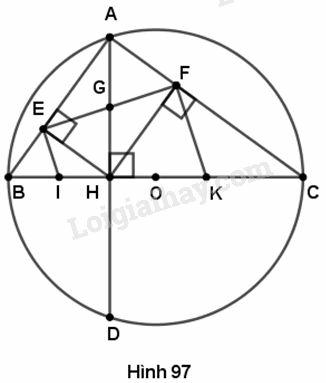
a) Đường tròn có bán kính là
Đường tròn có bán kính là
Ta có nên hai đường tròn tiếp xúc trong.
- Đường tròn có bán kính là
Đường tròn có bán kính là
Ta có nên hai đường tròn tiếp xúc trong.
- Đường tròn có bán kính là
Đường tròn có bán kính là
Ta có nên hai đường tròn tiếp xúc ngoài.
b) vì tam giác nội tiếp đường tròn đường kính
vì vì
Tứ giác có ba góc vuông nên là hình chữ nhật.
c) Tam giác vuông tại đường cao nên
Tam giác vuông tại đường cao nên
Từ (1) và (2) suy ra
d) Ta cần chứng minh và
Gọi là giao điểm của và ta có là hình chữ nhật (theo câu b), do đó mà nên suy ra
Tam giác cân tại nên
Từ (3) và (4) suy ra tức là
Ta lại có nên
Đường thẳng vuông góc với bán kính tại nên là tiếp tuyến của
Chứng minh tương tự, là tiếp tuyến của
Vậy là tiếp tuyến chung của hai đường tròn và
e) Theo tính chất hình chữ nhật,
Đường kính vuông góc với dây nên
Suy ra
Do đó lớn nhất lớn nhất. Ta có là dây của đường tròn do đó lớn nhất khi là đường kính , khi đó điểm trùng với điểm
Vậy khi dây vuông góc với tại điểm thì có độ dài lớn nhất.
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài, . Tiếp tuyến chung trong tại A cắt BC ở điểm M. Gọi E là giao điểm của OM và AB, F là giao điểm của O’M và AC. Chứng minh rằng:
a) Tứ giác AEMF là hình chữ nhật
b) ME.MO = MF.MO’
c) OO’ là tiếp tuyến của đường tròn có đường kính là BC
d) BC là tiếp tuyến của đường tròn có đường kính là OO’
Phương pháp giải:
a) Dùng tính chất hai tiếp tuyến cắt nhau, chứng minh tứ giác có ba góc vuông.
b) Dùng hệ thức lượng trong tam giác vuông
c) Chứng minh vuông góc với bán kính của đường tròn đường kính tại tiếp điểm.
d) Dùng tính chất của đường trung bình trong tam giác.
Chứng minh vuông góc với bán kính của đường tròn đường kính tại tiếp điểm.
Trả lời:
a)
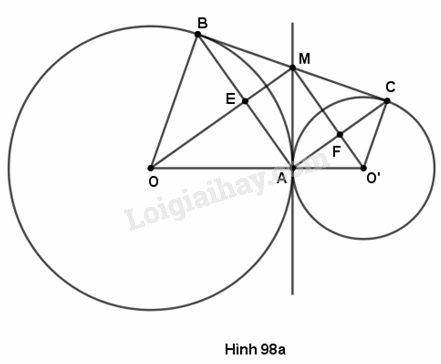
(h. 98a) Theo tính chất hai tiếp tuyến cắt nhau của đường tròn ta có là tia phân giác của
Tam giác cân tại có là tia phân giác nên
Chứng minh tương tự với đường tròn ta có là tia phân giác của nên
Do và là hai tia phân giác của hai góc kề bù nên
Tứ giác có ba góc vuông nên là hình chữ nhật.
b) Tam giác vuông tại đường cao nên
Tam giác vuông tại đường cao nên
Từ (1) và (2) suy ra
c) Đường tròn đường kính có tâm bán kính Ta có (vì là tiếp tuyến của đường tròn và ).
Đường thẳng vuông góc với bán kính của đường tròn tại nên là tiếp tuyến của đường tròn tức là tiếp tuyến của đường tròn có đường kính là
d)
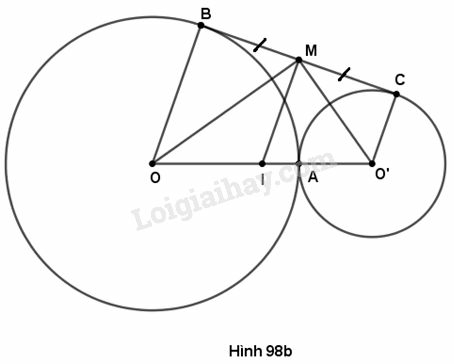
(h. 98b) Gọi I là trung điểm của
Đường tròn đường kính có tâm là bán kính là (vì là đường trung tuyến ứng với cạnh huyền của tam giác vuông nên )
Hình thang có nên là đường trung bình, suy ra
Ta lại có nên
Đường thẳng vuông góc với bán kính của đường tròn tại nên là tiếp tuyến của đường tròn tức là tiếp tuyến của đường tròn có đường kính
Cho hai đường tròn (O ; R) và (O’ ; r) cắt nhau tại A và B (R > r). Gọi I là trung điểm của OO’. Kẻ đường thẳng vuông góc với IA tại A, đường thẳng này cắt các đường tròn (O) và (O’) theo thứ tự ở C và D (khác A).
a) Chứng minh rằng AC = AD
b) Gọi K là điểm đối xứng với điểm A qua I. Chứng minh rằng KB vuông góc với AB.
Phương pháp giải:
a) Áp dụng định lí về đường kính vuông góc với dây và định lí về đường trung bình của hình thang, chứng minh
b) Áp dụng tính chất hai đường tròn cắt nhau và tính chất đường trung bình trong tam giác để chứng minh.
Trả lời:
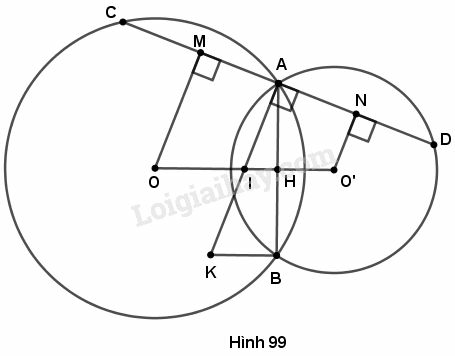
a) Kẻ ta có (vì cùng vuông góc với ).
Hình thang có và nên (đường thẳng đi qua trung điểm của một cạnh bên của hình thang và song song với hai cạnh đáy thì đi qua trung điểm của cạnh bên còn lại).
Theo định lí về đường kính vuông góc với dây, ta có :
nên
nên
Do nên
b) Gọi là giao điểm của và Theo tính chất của hai đường tròn cắt nhau, ta có
và
Tam giác có (vì đối xứng với điểm qua điểm ),
(chứng minh trên)
Nên là đường trung bình, suy ra tức là
Ta có và nên
Cho đường tròn (O), dây AB khác đường kính. Vẽ đường kính CD vuông góc với AB tại I (điểm D thuộc dây cung nhỏ AB). Gọi E là điểm đối xứng với D qua điểm I.
a) Tứ giác ADBE là hình gì ? Vì sao ?
b) Vẽ đường tròn (O’) đường kính EC. Hãy xác định vị trí tương đối của hai đường tròn (O) và (O’).
c) Gọi K là giao điểm của BC với đường tròn (O’), K khác C. Chứng minh rawmgf ba điểm A, E, K thẳng hàng.
d) Chứng minh rằng IK là tiếp tuyến của đường tròn (O’).
Phương pháp giải:
a) Dùng định lí đường kính vuông góc với dây thì đi qua trung điểm của dây đó, chứng minh tứ giác là hình bình hành có hai đường chéo vuông góc với nhau.
b) So sánh và tổng hoặc hiệu hai bán kính để tìm vị trí tương đối của hai hình tròn.
c) Vận dụng kiến thức : Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông , chứng minh
Áp dụng tiên đề Ơ-clit : Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó để chứng minh ba điểm cùng nằm trên một đường thẳng.
d) Dùng định lí : Nếu một đường thẳng là tiếp tuyến của một đường tròn thì đường thẳng đó vuông góc với bán kính đi qua tiếp điểm.
Trả lời:
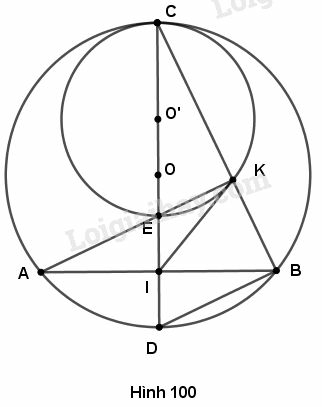
a) Đường kính vuông góc với dây nên
Điểm đối xứng với điểm qua điểm nên
Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
Hình bình hành có nên là hình thoi.
b) Đường tròn có bán kính là đường tròn có bán kính là Ta có nên hai đường tròn và có vị trí tiếp xúc trong.
c) Tam giác nội tiếp đường tròn đường kính nên
Tam giác nội tiếp đường tròn đường kính nên
Từ (1) và (2) suy ra
Tứ giác là hình thoi (câu a) nên
Qua ta có và cùng song song với nên thẳng hàng (theo tiên đề Ơ-clit).
d) Tam giác nội tiếp đường tròn đường kính nên suy ra Tam giác vuông tại có là đường trung tuyến ứng với cạnh huyền nên suy ra .
Tam giác cân tại (vì ) nên
Ta lại có (đối đỉnh) nên
Từ (3) và (4) suy ra tức là
Đường thẳng IK vuông góc với O'K tại điểm K nên IK là tiếp tuyến của (O)
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.