Toptailieu.vn giới thiệu Giải bài tập Toán 9 Ôn tập chương 2 chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Căn bậc hai lớp 9.
Giải bài tập Toán 9 Ôn tập chương 2
Trả lời câu hỏi giữa bài:
Trả lời phần câu hỏi 1 trang 126 SGK toán 9 tập 1: Thế nào là đường tròn ngoại tiếp một tam giác? Nêu cách xác định tâm của đường tròn ngoại tiếp tam giác.
Lời giải:
- Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác.
- Tâm đường tròn ngoại tiếp tam giác là giao điểm của các đường trung trực của các cạnh tam giác.
Trả lời phần câu hỏi 2 trang 126 SGK toán 9 tập 1: Thế nào là đường tròn nội tiếp một tam giác? Nêu cách xác định tâm của đường tròn nội tiếp tam giác.
Lời giải:
- Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác.
- Tâm đường tròn nội tiếp tam giác là giao điểm của các tia phân giác của các góc trong của tam giác.
Trả lời phần câu hỏi 3 trang 126 SGK toán 9 tập 1: Chỉ rõ tâm đối xứng của đường tròn, trục đối xứng của đường tròn.
Lời giải:
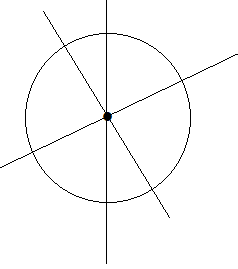
- Tâm của đường tròn là tâm đối xứng của đường tròn đó.
- Mọi đường kính của đường tròn đều là trục đối xứng của đường tròn.
Trả lời phần câu hỏi 4 trang 126 SGK toán 9 tập 1: Chứng minh định lí: Trong các dây của một đường tròn, dây lớn nhất là đường kính.
Lời giải:
Giả sử ta có đường tròn đường kính và một dây Ta chứng minh:
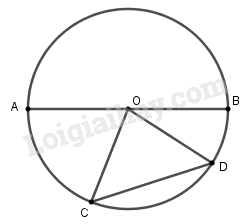
+) Nếu là đường kính thì
+) Nếu không là đường kính.
Trong ΔCOD, theo bất đẳng thức tam giác ta có:
mà
Vậy
Trả lời phần câu hỏi 5 trang 126 SGK toán 9 tập 1: Phát biểu các định lí về quan hệ vuông góc giữa đường kính và dây.
Lời giải:
Định lí: Nếu một đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy. Ngược lại, một đường kính đi qua trung điểm của một dây (không đi qua tâm) thì vuông góc với dây ấy.
Trả lời phần câu hỏi 6 trang 126 SGK toán 9 tập 1: Phát biểu các định lí về liên hệ giữa dây và khoảng cách từ tâm đến dây.
Lời giải:
Trong một đường tròn:
- Hai dây bằng nhau thì cách đều tâm và ngược lại, hai dây cách đều tâm thì bằng nhau.
- Dây lớn hơn thì gần tâm hơn và ngược lại, dây gần tâm hơn thì lớn hơn.
Trả lời phần câu hỏi 7 trang 126 SGK toán 9 tập 1: Nêu các vị trí tương đối của đường thẳng và đường tròn. Ứng với mỗi vị trí đó, viết hệ thức giữa d (khoảng cách từ tâm đến đường thẳng) và R (bán kính của đường tròn).
Lời giải:
| Vị trí tương đối của đường thẳng và đường tròn |
Số điểm chung |
Hệ thức giữa d và R |
| Đường thẳng và đường tròn cắt nhau |
2 |
d < R |
| Đường thẳng và đường tròn tiếp xúc nhau |
1 |
d = R |
| Đường thẳng và đường tròn không giao nhau |
0 |
d > R |
Trả lời phần câu hỏi 8 trang 126 SGK toán 9 tập 1: Phát biểu định nghĩa tiếp tuyến của đường tròn. Phát biểu tính chất của tiếp tuyến và dấu hiệu nhận biết tiếp tuyến. Phát biểu các tính chất của hai tiếp tuyến cắt nhau.
Lời giải:
Định nghĩa:
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua tiếp điểm ấy thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Tính chất và dấu hiệu nhận biết tiếp tuyến:
- Tiếp tuyến với đường tròn là đường thẳng chỉ có một điểm chung với đường tròn.
- Tiếp tuyến với đường tròn thì vuông góc với bán kính đi qua tiếp điểm.
Tính chất của hai tiếp tuyến cắt nhau.
Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:
a) Điểm đó cách đều hai tiếp điểm.
b) Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
c) Tia kẻ từ tâm qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.
Trả lời phần câu hỏi 9 trang 126 SGK toán 9 tập 1: Nêu các vị trí tương đồi của hai đường tròn. Ứng với mỗi vị trí đó, viết hệ thức giữa đoạn nối tâm d với các bán kính R, r.
Lời giải:

Trả lời phần câu hỏi 10 trang 126 SGK toán 9 tập 1: Tiếp điểm của hai đường tròn tiếp xúc nhau có vị trí như thế nào đối với đường nối tâm? Các giao điểm của hai đường tròn cắt nhau có vị trí như thế nào đối với đường nối tâm?
Lời giải:
- Tiếp điểm của hai đường tròn tiếp xúc với nhau thì nằm trên đường nối tâm.
- Các giao điểm của hai đường tròn cắt nhau thì đối xứng với nhau qua đường nối tâm.
Bài tập trang 128 SGK Toán 9
Bài 41 trang 128 SGK Toán 9 tập 1: Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.
Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.
a) Hãy xác định vị trí tương đối của các đường tròn: (I) và (O); (K) và(O); (I) và (K).
b) Tứ giác AEHF là hình gì? Vì sao?
c) Chứng minh đẳng thức
d) Chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K)
e) Xác định vị trí của điểm H để EF có độ dài lớn nhất.
Phương pháp giải:
a) Vị trí tương đối của hai đường tròn (O;R) và (O';r) ( )
- TH1: 2 đường tròn cắt nhau (có 2 điểm chung) khi và chỉ khi : R - r < OO' < R + r
- TH2: 2 đường tròn tiếp xúc nhau (1 điểm chung)
+) Tiếp xúc trong khi và chỉ khi OO' = R - r >0
+) Tiếp xúc ngoài khi và chỉ khi OO' = R + r
b) Chứng minh tứ giác có ba góc vuông dựa vào kiến thức : “Tiếp tuyến của đường tròn vuông góc với bán kính tại tiếp điểm."
c) Dùng hệ thức lượng về chiều cao và độ dài hình chiếu của các cạnh góc vuông lên cạnh huyền :
d) Chứng minh 1 đường thẳng là tiếp tuyến của 1 đường tròn thì ta chứng minh cho đường thẳng đó vuông góc với bán kính tại 1 điểm thuộc đường tròn.
e) Biểu diễn độ dài theo độ dài của rồi biện luận để tìm vị trí của dây đó vuông góc với .
Lời giải:
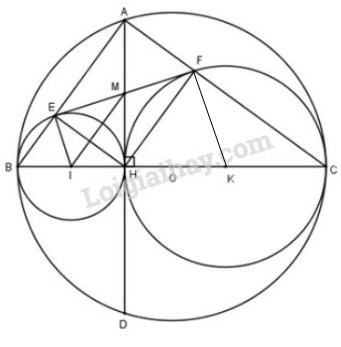
a) nên (I) tiếp xúc trong với (O)
nên (K) tiếp xúc trong với (O)
nên (I) tiếp xúc ngoài với (K)
b) Vì (gt)
Tương tự có ( do )
Và (do A thuộc đường tròn đường kính BC)
Tứ giác AEHF có nên là hình chữ nhật (Dấu hiệu nhận biết)
c) ∆ABH vuông tại H, HE là đường cao nên (hệ thức lượng trong tam giác vuông)
∆ACH vuông tại H, HF là đường cao nên (hệ thức lượng trong tam giác vuông)
Do đó (vì cùng bằng )
d) Gọi M là giao điểm của AH và EF, ta có: (do tứ giác AEHF là hình chữ nhật)
Xét ∆MEI và ∆MHI có:
, MI (cạnh chung)
Do đó (c.c.c)
(2 góc tương ứng)
mà (do ) nên
⇒ tại E mà IE là bán kính đường tròn (I)
⇒ ME hay EF là tiếp tuyến của đường tròn (I)
Chứng minh tương tự có EF là tiếp tuyến của đường tròn (K)
Hoặc ta chứng minh EF là tiếp tuyến của đường tròn (K) như sau:
Vì (cmt) nên tam giác MFH cân tại M ⇒ (*) (tính chất)
Vì (= bán kính đường tròn (K)) nên tam giác KFH cân tại K
⇒ (**) (tính chất)
Từ (*) và (**) ta có:
Hay (do )
⇒ tại F mà KF là bán kính đường tròn (K) nên EF là tiếp tuyến của đường tròn (K)
e) Cách 1:
Ta có (vì AEHF là hình chữ nhật) mà (=bán kính đường tròn (O)=R)
Do đó , không đổi. Dấu “=” xảy ra
Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.
Cách 2 câu e:
Xét đường tròn (O) có BC là đường kính và AD là dây cung mà tại H nên H là trung điểm của AD (định lý). Suy ra
Ta có (vì AEHF là hình chữ nhật)
⇒
Do đó EF lớn nhất khi AD lớn nhất. Khi đó, dây AD lớn nhất là đường kính.
Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.
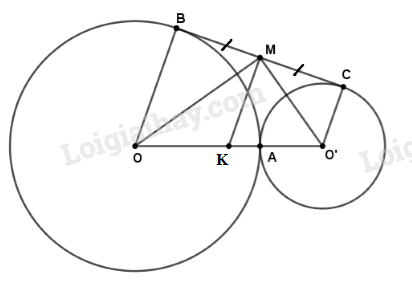
Bài 42 trang 128 SGK Toán 9 tập 1: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài. B ∈ (O), C ∈ (O’). Tiếp tuyến chung trong tại A cắt BC ở điểm M. Gọi E là giao điểm của OM và AB, F là giao điểm của O’M và AC. Chứng minh rằng
a) Tứ giác AEMF là hình chữ nhật.
b) ME.MO = MF.MO’
c) OO’ là tiếp tuyến của đường tròn có đường kính là BC.
d) BC là tiếp tuyến của đường tròn có đường kính là OO’.
Phương pháp giải:
a) Dùng tính chất hai tiếp tuyến cắt nhau, chứng minh tứ giác có ba góc vuông.
b) Dùng hệ thức lượng trong tam giác vuông
c) Chứng minh vuông góc với bán kính của đường tròn đường kính tại tiếp điểm.
d) Dùng tính chất của đường trung bình trong tam giác.
Chứng minh vuông góc với bán kính của đường tròn đường kính tại tiếp điểm.
Lời giải:
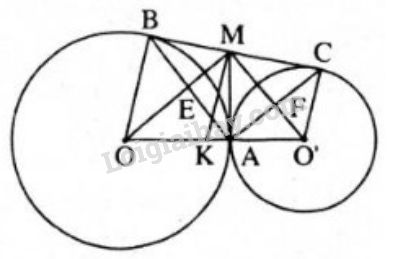
a) là các tiếp tuyến của đường tròn (O) (gt).
Theo tính chất của hai tiếp tuyến cắt nhau, ta có , MO là tia phân giác
Ta có: cân tại nên MO là đường phân giác đồng thời là đường cao
Lại có là các tiếp tuyến của đường tròn (O') (gt).
Theo tính chất của hai tiếp tuyến cắt nhau, ta có , MO’ là tia phân giác góc
Ta có: cân tại nên MO' là đường phân giác đồng thời là đường cao
Vì là tia phân giác của hai góc kề bù (hai tia phân giác của hai góc kề bù thì vuông góc với nhau)
Vì nên tứ giác AEMF là hình chữ nhật ( Tứ giác có 3 góc vuông)
b) vuông tại A có AE là đường cao nên (hệ thức lượng trong tam giác vuông)
vuông tại A có AF là đường cao nên (hệ thức lượng trong tam giác vuông)
Do đó,
c) Theo câu a) ta có và
⇒ nên M là tâm đường tròn đường kính BC có bán kính là MA. Mà tại A.
Do đó OO’ là tiếp tuyến của đường tròn đường kính BC
d)
Gọi K là trung điểm OO’, ta có K là tâm đường tròn có đường kính là OO’
Tam giác OMO' vuông tại M (do theo câu a có hay ) có MK là đường trung tuyến ứng với cạnh huyền OO' nên (tính chất)
Như vậy, đường tròn tâm K đường kính OO' có bán kính KM.
Ta có (do BC là tiếp tuyến)
⇒ Tứ giác OBCO’ là hình thang có K, M lần lượt là trung điểm các cạnh cạnh bên OO’, BC.
Do đó KM là đường trung bình của hình thang OBCO’
Mà nên
Ta có tại M nên BC là tiếp tuyến của đường tròn đường kính OO’.
Bài 43 trang 128 SGK Toán 9 tập 1: Cho hai đường tròn(O; R) và (O’; r) cắt nhau tại A và . Gọi I là trung điểm của OO’. Kẻ đường thẳng vuông góc với IA tại A, đường thẳng này cắt cá đường tròn tâm (O; R) và (O’; r) theo thứ tự tại C và D (khác A).
a) Chứng minh rằng AC = AD.
b) Gọi K là điểm đối xứng với điểm A qua điểm I. Chứng minh rằng KB vuông góc với AB
Phương pháp giải:
a) Áp dụng định lí về đường kính vuông góc với dây thì đi qua trung điểm dây đó và định lí về đường trung bình của hình thang.
b) Áp dụng tính chất hai đường tròn cắt nhau và tính chất đường trung bình trong tam giác để chứng minh.
Lời giải:
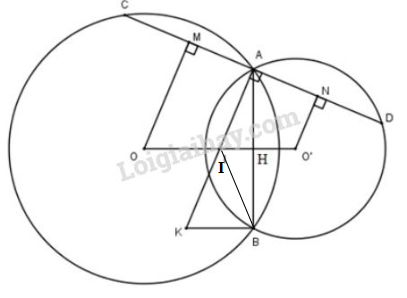
a) Vẽ OM ⊥ AC tại M, O’N ⊥AD tại N.
Xét đường tròn (O), vì (định lý đường kính vuông góc với dây)
Xét đường tròn (O'), vì (định lý đường kính vuông góc với dây)
Mặt khác, ta có
Suy ra tứ giác OMNO' là hình thang.
Hình thang OMNO’ có nên (đường thẳng song song với hai đáy của hình thang và đi qua trung điểm 1 cạnh bên thì đi qua trung điểm cạnh bên còn lại)
Do vậy hay
b) Ta có (O) và (O’) cắt nhau tại A, B
⇒ OO’ là đường trung trực của đoạn thẳng AB (tính chất đường nối tâm của hai đường tròn cắt nhau)
(tính chất đường trung trực của đoạn thẳng)
Mặt khác ( vì K đối xứng với A qua I)
Do đó:
Ta có ∆KBA có BI là đường trung tuyến và nên ∆KBA vuông tại B
Lý thuyết Ôn tập chương 2
1. Sự xác định đường tròn, tính chất đối xứng của đường tròn.
a) Đường tròn tâm bán kính là hình gồm các điểm cách điểm một khoảng bằng .
b) Vị trí tương đối của một điểm đối với một đường tròn.
Cho đường tròn và điểm .
+) nằm trên đường tròn
+) nằm trong đường tròn
+) nằm ngoài đường tròn
c) Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn.
d) Tính đối xứng của đường tròn.
+) Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó.
+) Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn.
2. Quan hệ đường kính và dây cung.
a) So sánh độ dài của đường kính và dây: Trong các dây của đường tròn, dây lớn nhất là đường kính.
b) Quan hệ vuông góc giữa đường kính và dây.
+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
c) Liên hệ giữa dây và khoảng cách từ tâm đến dây.
* Trong một đường tròn:
- Hai dây bằng nhau thì cách đều tâm.
- Hai dây cách đều tâm thì bằng nhau.
* Trong hai dây của một đường tròn:
- Dây nào lớn hơn thì dây đó gần tâm hơn .
- Dây nào gần tâm hơn thì dây đó lớn hơn.
3. Vị trí tương đối của đường thẳng và đường tròn.
Cho đường tròn và đường thẳng Đặt Ta có: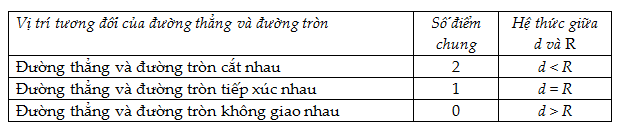
b) Khi đường thẳng và đường tròn tiếp xúc nhau thì đường thẳng được gọi là tiếp tuyến của đường tròn. Điểm chung của đường thẳng và đường tròn gọi là tiếp điểm.
4. Dấu hiệu nhận biết tiếp tuyến
+) Nếu một đường thẳng là tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm .
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là tiếp tuyến của đường tròn.
5. Tính chất hai tiếp tuyến cắt nhau
a) Tính chất hai tiếp tuyến cắt nhau
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
+) Điểm đó cách đều hai tiếp điểm.
+) Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
+) Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
b) Đường tròn nội tiếp tam giác
* Đường tròn tiếp xúc với ba cạnh của tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn.
* Tâm của đường tròn nội tiếp tam giác là giao của các đường phân giác của các góc trong tam giác.
c) Đường tròn bàng tiếp tam giác
* Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia gọi là đường tròn bàng tiếp tam giác.
* Với một tam giác, có ba đường tròn bàng tiếp.
* Tâm của đường tròn bàng tiếp tam giác trong góc là giao điểm của hai đường phân giác các góc ngoài tại và hoặc là giao điểm của phân giác trong góc và phân giác ngoài tại (hoặc
6. Vị trí tương đối của hai đường tròn
a) Tính chất đường nối tâm
* Đường nối tâm của hai đường tròn là trục đối xứng của hình gồm cả hai đường tròn đó.
* Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm.
* Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.
b) Vị trí tương đối của hai đường tròn
Cho hai đường tròn và . Đặt Ta có:
c) Tiếp tuyến chung của hai đường tròn
- Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với cả hai đường tròn đó.
- Tiếp tuyến chung ngoài là tiếp tuyến chung không cắt đoạn nối tâm.
- Tiếp tuyến chung trong là tiếp tuyến chung cắt đoạn nối tâm.