Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 VBT Toán lớp 9 Bài 2. Đường kính và dây của đường tròn trang 114,115 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:

VBT Toán lớp 9 Bài 2. Đường kính và dây của đường tròn

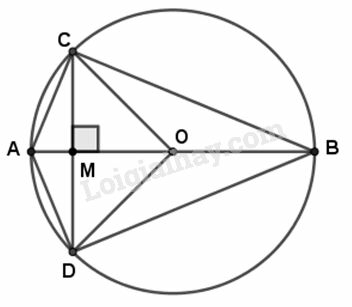
(A) Tam giác ACD là tam giác cân (Đúng vì tam giác có AM vừa là đường cao vừa là đường trung tuyến).

(B) Tam giác ABC là tam giác cân (Sai vì tam giác  vuông tại ).

(C) Tam giác BCD là tam giác cân (Đúng vì tam giác có  vừa là đường cao vừa là đường trung tuyến).

(D) Tam giác ABD là tam giác cân (Sai vì tam giác  vuông tại )

(E) Tam giác OCD là tam giác cân (Đúng vì tam giác có hai cạnh ).

Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:

a) Bốn điểm B, E, D, C thuộc cùng một đường tròn

b) DE < BC. 

Phương pháp giải:

a) Tìm một điểm cách đều bốn điểm 

b) Dùng định lí : Trong các dây của đường tròn, đường kính là dây lớn nhất.

Trả lời:

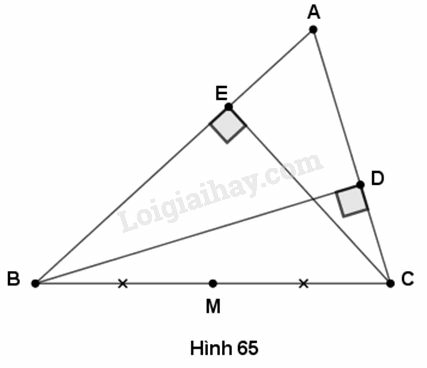
a) Gọi  là trung điểm của  Theo tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông, ta có 

suy ra  hay bốn điểm  cách đều điểm M

Do đó bốn điểm  thuộc một đường tròn có đường kính là 

b) Trong đường tròn  nói trên,  là một dây không đi qua tâm,  là đường kính nên (vì trong các dây của đường tròn, dây lớn nhất là đường kính)

Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK

Gợi ý: Kẻ OM vuông góc với CD.

Phương pháp giải:

Vận dụng kiến thức : Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây đó.

Trả lời:

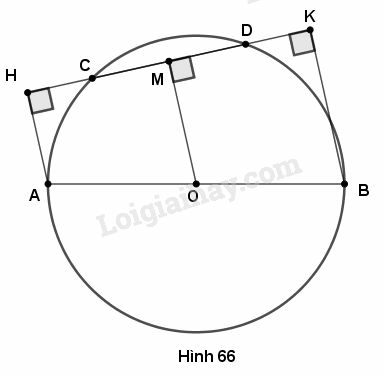
Kẻ  Ta có  nên 

Hình thang  có  và  nên              (1)

Đường kính chứa  vuông góc với dây  nên  (đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy).                                (2)

Từ  và  suy ra  tức là 

Cho đường tròn (O) đường kính  dây  Vẽ dây CD vuông góc với AB tại H.

a) Tam giác ABC là tam giác gì ? Vì sao ?

b) Tam giác BCD là tam giác gì ? Vì sao ?

c) Tính các độ dài AH, CD.

Phương pháp giải:

a) Dùng định lí : Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.

b) Chứng minh tam giác có đường cao cũng là đường trung tuyến.

c) Dùng hệ thức về cạnh và đường cao trong tam giác vuông : Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.

Trả lời:

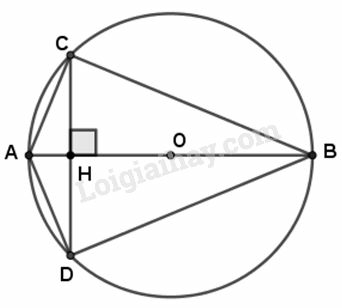
a) Tam giác  vuông tại  vì tam giác  có  là đường kính của 

(tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông).

b) Đường kính  vuông góc với  nên  (Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây đó ).

Tam giác  có đường cao  cũng là đường trung tuyến nên tam giác đó cân tại 

c) Tam giác  vuông tại  đường cao  nên  tức là 

Suy ra 

Áp dụng định lí Py-ta-go vào tam giác vuông  ta tính được

 nên 

Suy ra