Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây trang 116,117,118,119 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:
VBT Toán lớp 9 Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
Phần câu hỏi bài 3 trang 116 Vở bài tập toán 9 tập 1
Câu 5
Hãy khoanh trong vào chữ cái đứng trước đáp án đúng.
Cho tam giác ABC. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, BC, CA và O là giao điểm của các đường trung trực của tam giác đó. Biết rằng OD > OE > OF. Khi đó ta có:
(A) AB > BC > AC
(B) BD > AC > AB
(C) AB < BC < AC
(D) BC < AC <AB
Phương pháp giải:
Vận dụng kiến thức : Dây nào lớn hơn thì dây đó gần tâm hơn.
Trả lời:
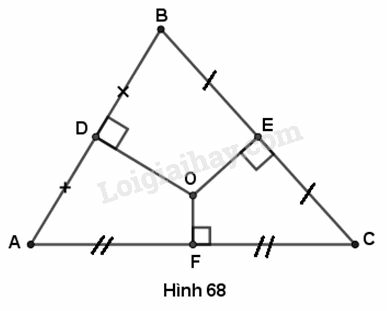
Vì
Chọn C.
Câu 6
Cho đường tròn (O) đường kính 10cm, dây AB cách tâm O một khoảng 3cm. Độ dài dây AB bằng:
(A) 4cm (B) 6cm
(C) 8cm (D) 10cm
Phương pháp giải:
- Vẽ hình theo giả thiết đã cho.
- Gọi khoảng cách từ tâm đến dây là
- Áp dụng định lí Py-ta-go và định lí đường kính vuông góc với một dây thì đi qua trung điểm của dây đó để tìm
Trả lời:
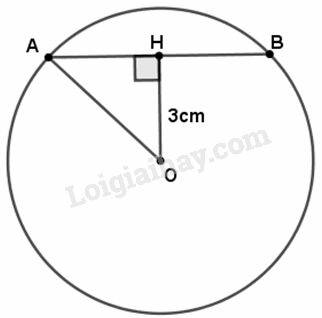
Đường tròn có đường kính là nên
Từ kẻ đường thẳng vuông góc với dây , cắt dây tại
Khi đó, là khoảng cách từ tâm đến dây
Tam giác vuông theo định lí Py-ta-go ta có :
Đường kính của đường tròn tâm chứa vuông góc với nên (định lí trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây đó)
Vậy
Chọn C.
a) Tính khoảng cách từ tâm O đến dây AB
b) Gọi I là điểm thuộc dây AB sao cho Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh rằng
Phương pháp giải:
a) Dùng định lí về đường kính vuông góc với một dây.
b) Dùng định lí về sự liên hệ giữa dây và khoảng cách từ tâm đến dây.
Trả lời:
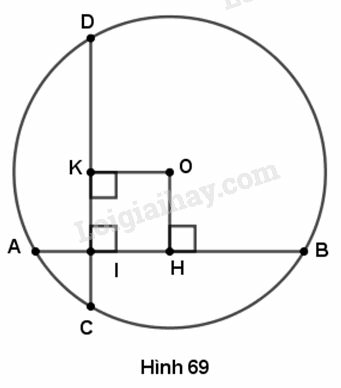
a) Kẻ Đường kính chứa vuông góc với nên
Tính Áp dụng định lí Py-ta-go, ta có :
nên
b) Kẻ Tứ giác có nên là hình chữ nhật.
Do đó
Ta có nên (hai dây cách đều tâm thì bằng nhau).
Cho đường tròn (O) có các dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm E nằm bên ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Chứng minh rằng:
a) EH = EK
b) EA = EC.
Phương pháp giải:
a) Dùng phương pháp hai tam giác bằng nhau.
b) Chứng minh và kết hợp với câu a.
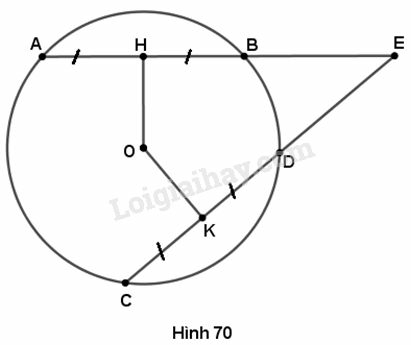
Trả lời:
a) Ta có nên
Ta có nên (vì hai dây bằng nhau thì cách đều tâm).
Các tam giác vuông và có là cạnh chung, (chứng minh trên).
Do đó, (trường hợp cạnh huyền – cạnh góc vuông ). Suy ra
b) Ta có mà nên
Từ và suy ra tức là
Cho đường tron (O). Gọi AC, AD là hai dây bằng nhau của đường tròn, AB là đường kính. Chứng minh rằng
a) AO là tia phân giác của góc CAD.
b) AB vuông góc với CD.
Phương pháp giải:
a) Dùng kiến thức: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó và định lí “Trong một đường tròn, hai dây bằng nhau thì cách đều tâm”.
b) Sử dụng chứng minh a và chứng minh tiếp
Trả lời:
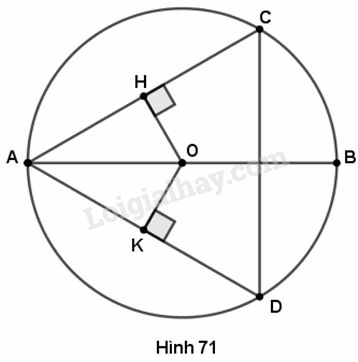
a) Kẻ
Ta có nên (vì hai dây bằng nhau thì cách đều tâm).
Do đó là tia phân giác của
b) Tam giác có nên là tam giác cân. Ta lại có là tia phân giác của nên
Vậy
Cho hình 72 trong đó hai đường tròn có cùng tâm O. Cho biết AB > CD. Hãy so sánh các độ dài:
a) OH và OK
b) ME và MF
c) MH và MK
Phương pháp giải:
Dùng định lí dây nào lớn hơn thì gần tâm hơn và ngược lại.
Trả lời:
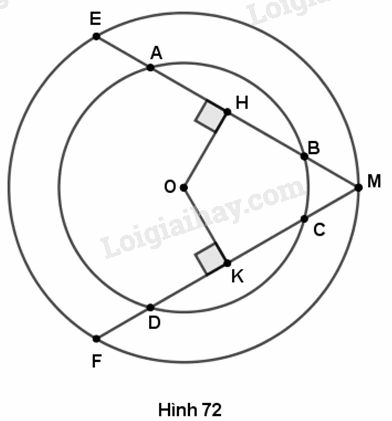
a) Xét đường tròn nhỏ, và là khoảng cách từ tâm đến các dây và CD.
Do (giả thiết) nên (vì dây lớn hơn thì gần tâm hơn).
b) Xét đường tròn lớn, khoảng cách từ tâm đến các dây và MF là và OK.
Do (câu a) nên (vì dây gần tâm hơn thì lớn hơn).
c) Xét đường tròn lớn, do nên ( đường kính vuông góc với dây thì đi qua trung điểm của dây)
Tương tự, do nên
Ta lại có (câu b) nên
Bài 13 trang 119 Vở bài tập toán 9 tập 1
Cho đường tròn tâm (O), điểm A nằm bên ngoài vòng tròn. Vẽ dây BC vuông góc với OA tại A. Vẽ dây EF bất kì đi qua A và không vuông góc với OA. So sánh độ dài hai dây BC và EF.
Phương pháp giải:
- Dùng kiến thức về mối quan hệ giữa cạnh huyền và cạnh góc vuông trong một tam giác vuông và định lí “trong một đường tròn dây nào lớn hơn thì gần tâm hơn”.
Trả lời:
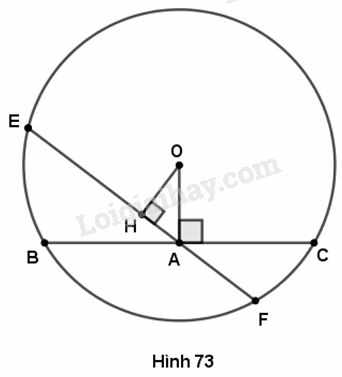
Kẻ Ta có khoảng cách từ tâm đến dây là , khoảng cách từ tâm đến dây là .
Xét tam giác vuông tại ta có :
(vì trong tam giác vuông, cạnh huyền lớn hơn cạnh góc vuông).
Do nên (vì dây gần tâm hơn thì lớn hơn).
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.