Toptailieu.vn xin giới thiệu 50 bài tập trắc nghiệm Sự xác định của đường tròn - Tính chất đối xứng của đường tròn (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 9 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
Sự xác định của đường tròn - Tính chất đối xứng của đường tròn
Câu 1: Số tâm đối xứng của đường tròn là:
A. 1
B. 2
C. 3
D. 4
Lời giải:
Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.
Nên đường tròn có một tâm đối xứng duy nhất là tâm của đường tròn.
Đáp án cần chọn là: A
Câu 2: Tâm đối xứng của đường tròn là:
A. Điểm bất kì bên trong đường tròn
B. Điểm bất kì bên ngoài đường tròn
C. Điểm bất kì trên đường tròn
D. Tâm của đường tròn
Lời giải:
Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.
Nên đường tròn có một tâm đối xứng duy nhất là tâm của đường tròn.
Đáp án cần chọn là: D
Câu 3: Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn?
A. Đường tròn không có trục đối xứng
B. Đường tròn có duy nhất một trục đối xứng là đường kính.
C. Đường tròn có hai trục đối xứng là hai đường kính vuông góc với nhau.
D. Đường tròn có vô số trục đối xứng là đường kính
Lời giải:
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn
Nên đường tròn có vô số trục đối xứng
Đáp án cần chọn là: D
Câu 4: Điền từ thích hợp vào chỗ trống: “Đường tròn có … trục đối xứng”
A. 1
B. 2
C. Vô số
D. 3
Lời giải:
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn
Nên đường tròn có vô số trục đối xứng
Đáp án cần chọn là: C
Câu 5: Tâm đường tròn ngoại tiếp tam giác là:
A. Giao của ba đường phân giác
B. Giao của ba đường trung trực
C. Giao của ba đường cao
D. Giao của ba đường trung tuyến.
Lời giải:
Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó.
Đáp án cần chọn là: B
Câu 6: Giao ba đường trung trực của tam giác là:
A. Tâm đường tròn ngoại tiếp tam giác (đường tròn đi qua ba đỉnh của tam giác)
B. Tâm đường tròn nội tiếp tam giác (đường tròn tiếp xúc với ba cạnh của tam giác)
C. Tâm đường tròn cắt ba cạnh của tam giác
D. Tâm đường tròn đi qua 1 đỉnh và cắt hai cạnh của tam giác
Lời giải:
Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó.
Đáp án cần chọn là: A
Câu 7: Cho đường tròn (O; R) và điểm M bất kỳ, biết rằng OM = R. Chọn khẳng định đúng?
A. Điểm M nằm ngoài đường tròn
B. Điểm M nằm trên đường tròn
C. Điểm M nằm trong đường tròn
D. Điểm M không thuộc đường tròn
Lời giải:
Cho điểm M và đường tròn (O; R) ta so sánh khoảng cách OM với bán kính R để xác định vị trí tương đối theo bảng sau:
Đáp án cần chọn là: B
Câu 8: Cho đường tròn (O; R) và điểm M bất kỳ, biết rằng OM > R. Chọn khẳng định đúng?
A. Điểm M nằm ngoài đường tròn
B. Điểm M nằm trên đường tròn
C. Điểm M nằm trong đường tròn
D. Điểm M không thuộc đường tròn
Lời giải:
Vì OM > R nên điểm M nằm bên ngoài đường tròn
Đáp án cần chọn là: A
Câu 9: Xác định tâm và bán kính của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh a.
Lời giải:
Gọi O là giao hai đường chéo của hình vuông ABCD. Khi đó theo tính chất của hình vuông ta có OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính R = OA =
Xét tam giác ABC vuông cân tại B ta có:
Vậy tâm đường tròn ngoại tiếp hình vuông ABCD cạnh a là giao điểm hai đường chéo, bán kính là
Đáp án cần chọn là: C
Câu 10: Tính bán kính R của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh 3cm
Lời giải:
Gọi O là giao hai đường chéo của hình vuông ABCD. Khi đó theo tính chất của hình vuông ta có OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính
Xét tam giác ABC vuông cân tại B ta có AC2 = AB2 + BC2 = 32 + 32 = 18
Đáp án cần chọn là: B
Câu 11: Tâm của đường tròn ngoại tiếp tam giác vuông là:
A. Trung điểm cạnh huyền
B. Trung điểm cạnh góc vuông lớn hơn
C. Giao ba đường cao
D. Giao ba đường trung tuyến
Lời giải:
Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.
Đáp án cần chọn là: A
Câu 12: Chọn câu đúng. Bán kính của đường tròn ngoại tiếp tam giác vuông?
A. bằng cạnh nhỏ nhất của tam giác vuông
B. bằng nửa cạnh góc vuông lớn hơn
C. bằng nửa cạnh huyền
D. bằng 4cm
Lời giải:
Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp. Do đó bán kính đường tròn ngoại tiếp tam giác vuông bằng nửa cạnh huyền
Đáp án cần chọn là: C
Câu 13: Cho tam giác ABC có các đường cao BD, CE. Biết rằng bốn điểm B, E, D, C cùng nằm trên một đường tròn. Chỉ rõ tâm và bán kính của đường tròn đó.
A. Tâm là trọng tâm tam giác ABC và bán kính 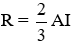
B. Tâm là trunng điểm AB và bán kính
C. Tâm là giao điểm của BD và EC, bán kính
D. Tâm là trung điểm BC và bán kính
Lời giải:
Gọi I là trung điểm của BC.
Xét tam giác BEC vuông tại E có EI = IB = IC = 
Xét tam giác BDC vuông tại D có DI = IB = IC = 
Từ đó ta có ID = IE = IB = IC = 
Đáp án cần chọn là: D
Câu 14: Cho tam giác ABC có các đường cao BD, CE. Chọn khẳng định đúng.
A. Bốn điểm B, E, D, C cùng nằm trên một đường tròn
B. Năm điểm A, B, E, D, C cùng nằm trên một đường tròn
C. Cả A, B, đều sai
D. Cả A, B đều đúng
Lời giải:
Gọi I là trung điểm BC.
Xét tam giác BEC vuông tại E có EI = IB = IC = 
Xét tam giác BDC vuông tại D có DI = IB = IC = 
Từ đó ta có ID = IE = IB = IC = 
Ta thấy IA > ID nên điểm A không thuộc đường tròn trên
Đáp án cần chọn là: A
Câu 15: Trên mặt phẳng tọa độ Oxy, xác định vị trí tương đối của điểm A (−1; −1) và đường tròn tâm là gốc tọa độ O, bán kính R = 2
A. Điểm A nằm ngoài đường tròn
B. Điểm A nằm trên đường tròn
C. Điểm A nằm trong đường tròn
D. Không kết luận được
Lời giải:
Ta có 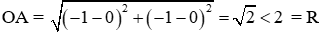
Đáp án cần chọn là: C
Câu 16: Trên mặt phẳng tọa độ Oxy, xác định vị trí tương đối của điểm A (−3; −4) và đường tròn tâm là gốc tọa độ O, bán kính R = 3
A. Điểm A nằm ngoài đường tròn
B. Điểm A nằm trên đường tròn
C. Điểm A nằm trong đường tròn
D. Không kết luận được
Lời giải:
Ta có 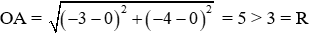
Đáp án cần chọn là: A
Câu 17: Cho tam giác ABC vuông tại A, có AB = 15cm; AC = 20cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Lời giải:
Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền BC, bán kính
Đáp án cần chọn là: B
Câu 18: Cho tam giác ABC vuông tại A, có AB = 5cm; AC = 12cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Lời giải:
Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền BC, bán kính
Đáp án cần chọn là: C
Câu 19: Cho tam giác đều ABC cạnh bằng 2cm. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.
Lời giải:
Gọi I là trung điểm của BC, G là trọng tâm tam giác ABC và R là bán kính đường tròn ngoại tiếp tam giác ABC thì
Đáp án cần chọn là: C
Câu 20: Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Tính bán kính đường tròn đi qua bốn đỉnh A, B, C, D
A. R = 7,5 cm
B. R = 13cm
C. R = 6cm
D. R = 6,5cm
Lời giải:
Gọi I là giao hai đường chéo, ta có IA = IB = IC = ID (vì BD = AC và I là trung điểm mỗi đường)
Nếu bốn điểm A, B, C, D cùng thuộc đường tròn tâm I bán kính
Theo định lý Pytago trong tam giác vuông ABC ta có:
Vậy bán kính cần tìm là R = 6,5cm
Đáp án cần chọn là: D
Câu 21: Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Tính bán kính đường tròn đi qua bốn đỉnh A, B, C, D
A. R = 5cm
B. R = 10cm
C. R = 6cm
D. R = 2,5cm
Lời giải:
Gọi I là giao hai đường chéo, ta có IA = IB = IC = ID (vì BD = AC và I là trung điểm mỗi đường)
Nếu bốn điểm A, B, C, D cùng thuộc đường tròn tâm I bán kính
Theo định lý Pytago trong tam giác vuông ABC ta có
Vậy bán kính cần tìm là R = 5cm
Đáp án cần chọn là: A
Câu 22: Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của AB, AC. Gọi E là giao điểm của CM và DN. Tâm của đường tròn đi qua bốn điểm A, D, E, M là?
A. Trung điểm của DM
B. Trung điểm của DB
C. Trung điểm của DE
D. Trung điểm của DA
Lời giải:
Do đó bốn điểm A, D, E, M cùng thuộc đường tròn tâm I bán kính
Đáp án cần chọn là: A
Câu 23: Cho hình vuông ABCD cạnh 4cm. Gọi M, N lần lượt là trung điểm của AB, BC. Gọi E là giao điểm của AM và DN. Bán kính của đường tròn đi qua bốn điểm A, D, E, M là?
A. R = 5 cm
B. R = 10 cm
C. R = 2√5 cm
D. R = √5 cm
Lời giải:
+) Ta có góc CDN = góc ECN (vì cùng phụ với góc CNE)
+) Gọi I là trung điểm của DM
Do đó bốn điểm A, D, E, M cùng thuộc đường tròn tâm I bán kính
Suy ra bán kính đường tròn đi qua 4 điểm A, D, E, M là:
Đáp án cần chọn là: D
Câu 24: Cho tam giác ABC cân tại A, đường cao AH = 2cm, BC = 8cm. Đường vuông góc với AC tại C cắt đường thẳng AH ở D.
Các điểm nào sau đây cùng thuộc một đường tròn?
A. D, H, B, C
B. A, B, H, C
C. A, B, D, H
D. A, B, D, C
Lời giải:
Ta có ΔABC cân tại A có đường cao AH nên AH cũng là đường phân giác
Suy ta ΔACD = ΔABD (c – g – c) nên
Lấy I là trung điểm AD. Xét hai tam giác vuông ABD và ACD có
Nên I là điểm cách đều A, B, D, C hay A, B, D, C cùng nằm trên đường tròn tâm I, đường kính AD
Đáp án cần chọn là: D
Vận dụng: Cho tam giác ABC cân tại A, đường cao AH = 2cm, BC = 8cm. Đường vuông góc với AC tại C cắt đường thẳng AH ở D.
Tính đường kính của đường tròn đi qua các điểm A, B, D, C
A. d = 8cm
B. d = 12cm
C. d = 10cm
D. d = 5cm
Lời giải:
Ta có ΔABC cân tại A có đường cao AH nên AH cũng là đường phân giác
Suy ta ΔACD = ΔABD (c – g – c) nên
Lấy I là trung điểm AD. Xét hai tam giác vuông ABD và ACD có
Nên I là điểm cách đều A, B, D, C hay A, B, D, C cùng nằm trên đường tròn tâm I, đường kính AD
Do đó ta cần tính độ dài AD
Vì BC = 8cm ⇒ BH = 4cm. Áp dụng định lý Pytago cho tam giác vuông AHB ta được:
Áp dụng hệ thức lượng trong tam giác vuông ABD ta có AB2 = AH. AD
Vậy đường kính cần tìm là 10cm
Đáp án cần chọn là: C
Câu 25: Cho tam giác ABC cân tại A, đường cao AH = 4cm, BC = 6cm. Đường vuông góc với AC tại C cắt đường thẳng AH ở D
Chọn câu đúng:
A.
B. DC = DB
C. Bốn điểm A, B, D, C cùng thuộc một đường tròn
D. Cả A, B, C đều đúng
Lời giải:
Ta có ΔABC cân tại A có đường cao AH nên AH cũng là đường phân giác
Suy ta ΔACD = ΔABD (c – g – c) nên 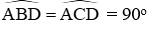
Lấy I là trung điểm AD. Xét hai tam giác vuông ABD và ACD có
Nên I là điểm cách đều A, B, D, C hay A, B, D, C cùng nằm trên đường tròn tâm I, đường kính AD nên đáp án C đúng
Đáp án cần chọn là: D
Câu 26: Cho tam giác ABC cân tại A, đường cao AH = 4cm, BC = 6cm. Đường vuông góc với AC tại C cắt đường thẳng AH ở D
Tính đường kính của đường tròn đi qua các điểm A, B, D, C
A. d = 6,25cm
B. d = 12,5cm
C. d = 6cm
D. d = 12cm
Lời giải:
Ta có ΔABC cân tại A có đường cao AH nên AH cũng là đường phân giác
Suy ta ΔACD = ΔABD (c – g – c) nên 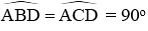
Lấy I là trung điểm AD. Xét hai tam giác vuông ABD và ACD có
Nên I là điểm cách đều A, B, D, C hay A, B, D, C cùng nằm trên đường tròn tâm I, đường kính AD.
Do đó ta cần tính độ dài AD
Vì BC = 6cm ⇒ BH = 3cm. Áp dụng định lý Pytago cho tam giác vuông AHB ta được
Áp dụng hệ thức lương trong tam giác vuông ABD ta có:
Vậy đường kính cần tìm là 6,25cn
Đáp án cần chọn là: A
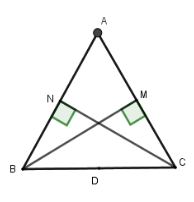
Câu 27: Cho tam giác đều ABC cạnh bằng a, các đường cao là BM và CN. Gọi D là trung điểm cạnh BC. Đường tròn đi qua bốn điểm B, N, M, C là:
Lời giải:
Gọi D là trung điểm BC
Xét hai tam giác vuông BNC và BMC có ND, MD là hai đường trung tuyến
⇒ DN = DB = DC = DM = 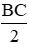
Đáp án cần chọn là: A
Câu 28: Cho tam giác đều ABC cạnh bằng a, các đường cao là BM và CN. Gọi D là trung điểm cạnh BC. Gọi G là giao điểm của BM và CN. Xác định vị trí tương đối của điểm G và điểm A với đường tròn đi qua bốn điểm B, N, M, C.
A. Điểm G nằm ngoài đường tròn; điểm A nằm trong đường tròn
B. Điểm G nằm trong đường tròn; điểm A nằm ngoài đường tròn
C. Điểm G và A cùng nằm trên đường tròn
D. Điểm G và A cùng nằm ngoài đường tròn
Lời giải:
Gọi D là trung điểm BC
Xét hai tam giác vuông BNC và BMC có ND, MD là hai đường trung tuyến
⇒ DN = DB = DC = DM = 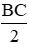
Do đó ta xác định được vị trí tương đối của điểm G với đường tròn tâm D bán kính
Gọi cạnh của tam giác đều ABC là a (a > 0)
Ta có G là trực tâm ΔABC nên G cũng là trọng tâm ΔABC suy ra
D là trung điểm BC
Theo định lý Pytago cho tam giác vuông ADC ta có:
Nhận thấy 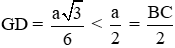
Và 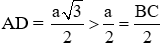
Đáp án cần chọn là: B
Câu 29: Cho tam giác đều ABC cạnh bằng 3cm, các đường cao là BM và CN. Gọi O là trung điểm cạnh BC. Bốn điểm nào sau đây cùng thuộc một đường tròn
A. B, N, M, C
B. A, B, M, N
C. A, C, M, N
D. Cả A, B, C đều sai
Lời giải:
Đáp án cần chọn là: A
Câu 30: Tính bán kính đường tròn đi qua bốn điểm A, N, G, M với G là giao của BM và CN
Lời giải:
Vì G là giao điểm của hai đường cao BM, CN nên G là trực tâm ΔABC
Ta có G là trực tâm ABC nên G cũng là trọng tâm ΔABC suy ra
D là trung điểm BC
Theo định lý Pytago cho tam giác vuông ADC ta có:
Gọi I là trung điểm của AG. Xét tam giác vuông ANG có IN = IA = IG, xét tam giác vuông AMG có IM = IA = IG nên:
Hay 4 điểm A, N, G, M cùng thuộc một đường tròn bán kính
Đáp án cần chọn là: D
Câu 31: Cho tam giác đều ABC cạnh bằng 3cm, các đường cao là BM và CN. Gọi O là trung điểm cạnh BC. Tính bán kính đường tròn đi qua bốn điểm A, N, G, M với G là giao điểm của BM và CN
Lời giải:
Vì G là giao điểm của hai đường cao BM, CN nên G là trực tâm ΔABC
Ta có G là trực tâm ΔABC nên G cũng là trọng tâm ΔABC suy ra
D là trung điểm BC
Theo định lý Pytago cho tam giác vuông ADC ta có:
Gọi I là trung điểm của AG. Xét tam giác vuông ANG có IN = IA = IG, xét tam giác vuông AMG có IM = IA = IG nên:
Hay 4 điểm A, N, G, M cùng thuộc một đường tròn bán kính
Đáp án cần chọn là: D
Câu 32: Số tâm đối xứng của đường tròn là:
A. 1
B. 2
C. 3
D. 4
Lời giải:
Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.
Nên đường tròn có một tâm đối xứng duy nhất là tâm của đường tròn.
Đáp án cần chọn là:A
Câu 33: Cho tam giác ABC vuông tại A, có AB = 5cm; AC = 12cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
A. R = 26
B. R = 13
C. R =
D. R = 6
Lời giải:
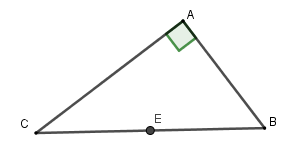
Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền BC,
bán kính R =
Theo định lý Pytago ta có
BC = = 13
nên bán kính R =
Đáp án cần chọn là:C
Câu 34: Xác định tâm và bán kính của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh a.
A. Tâm là giao điểm A và bán kính R = a
B. Tâm là giao điểm hai đường chéo và bán kính R = a
C. Tâm là giao điểm hai đường chéo và bán kính
D. Tâm là điêm B và bán kính là
Lời giải:
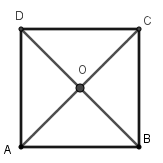
Gọi O là giao hai đường chéo của hình vuông ABCD. Khi đó theo tính chất của hình vuông ta có OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính R = OA =
Xét tam giác ABC vuông cân tại B ta có
AC2 = AB2 + BC2AC = a
Vậy tâm đường tròn ngoại tiếp hình vuông ABCD cạnh a là giao điểm hai đường chéo, bán kính là
Đáp án cần chọn là:C
Câu 35: Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của AB, AC. Gọi E là giao điểm của CM và DN. Tâm của đường tròn đi qua bốn điểm A, D, E, M là?
A. Trung điểm của DM
B. Trung điểm của DB
C. Trung điểm của DE
D. Trung điểm của DA
Lời giải:
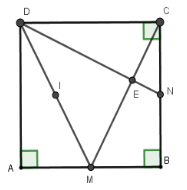
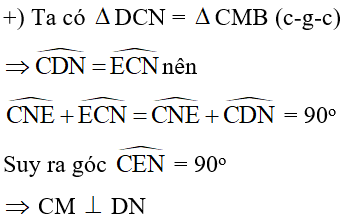


Câu 36: Cho tam giác đều ABC cạnh bằng a, các đường cao là BM và CN. Gọi D là trung điểm cạnh BC. Đường tròn đi qua bốn điểm B, N, M, C là:
A. Đường tròn tâm D bán kính
B. Đường tròn tâm D bán kính BC
C. Đường tròn tâm B bán kính
D. Đường tròn tâm C bán kính
Lời giải:


Câu 37: Đường tròn là hình:
A. Không có trục đối xứng
B. Có một trục đối xứng
C. Có hai trục đối xứng
D. Có vô số trục đối xứng
Lời giải:
Đáp án: D
Đáp án cần chọn là:D
Câu 38: Nếu tam giác có góc tù thì tâm đường tròn ngoại tiếp tam giác là điểm nằm ở:
A. Ngoài tam giác
B. Trong tam giác
C. Là trung điểm của cạnh nhỏ nhất
D. Là trung điểm của cạnh lớn nhất
Lời giải:
Đáp án: A
Đáp án cần chọn là:A
Câu 39: Tâm đường tròn ngoại tiếp tam giác là:
A. Giao của 3 đường trung tuyến
B. Giao của 3 đường phân giác
C. Giao của 3 đường trung trực
D. Giao của 3 đường cao
Lời giải:
Đáp án: C
Đáp án cần chọn là:C
Câu 40: Khẳng định nào sau đây sai?
A. Qua ba điểm không thẳng hàng , ta vẽ được một và chỉ một đường tròn .
B. Không vẽ được đường tròn nào đi qua ba điểm thẳng hàng
C. Tâm của đường tròn là tâm đối xứng của đường tròn đó .
D. Cả 3 khẳng định trên đều sai.
Lời giải:
Đáp án: D
Đáp án cần chọn là:D
Câu 41: Cho tam giác ABC, các đường cao BD và CE cắt nhau tại H. Câu nào sau đây đúng?
A. Bốn điểm B,E,D,C cùng nằm trên một đường tròn
B. Bốn điểm A,E,H,D cùng nằm trên một đường tròn
C. DE
D. Cả A, B, C đều đúng
Lời giải:
Đáp án: D
Đáp án cần chọn là:D
Câu 42: Cho đường tròn (O; R) và điểm M bất kỳ, biết rằng OM > R. Chọn khẳng định đúng?
A. Điểm M nằm ngoài đường tròn
B. Điểm M nằm trên đường tròn
C. Điểm M nằm trong đường tròn
D. Điểm M không thuộc đường tròn
Lời giải:
Giải thích: Vì OM > R nên điểm M nằm bên ngoài đường tròn
Đáp án cần chọn là:A
Câu 43: Cho tam giác ABC vuông tại A. Khi đó, tâm đường tròn ngoại tiếp tam giác ABC là?
A. Điểm A
B. Điểm B .
C. Chân đường cao hạ từ A
D. Trung điểm của BC
Lời giải:
Gọi M là trung điểm của BC.
Tam giác ABC vuông tại A có đường trung tuyến AM ứng với cạnh huyền BC nên:
Suy ra, điểm M là tâm đường tròn ngoại tiếp tam giác ABC
Đáp án cần chọn là:D
Câu 44: Cho tứ giác ABCD là hình bình hành và 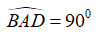
A. Trung điểm AC
B. Điểm A
C. Điểm B
D. Điểm D
Lời giải:
Vì tứ giác ABCD là hình bình hành và 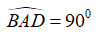
Gọi O là giao điểm hai đường chéo.
Theo tính chất hình chữ nhật ta có:
Do đó, O là tâm đường tròn ngoại tiếp hình chữ nhật ABCD.
Đáp án cần chọn là:A
Câu 45: Cho 4 điểm phân biệt A, B, C và D sao cho tam giác ABC vuông tại A và tam giác BCD vuông tại
D. Tìm tâm đường tròn ngoại tiếp tứ giác ABCD?
A. Điểm A
B. Điểm B
C. Trung điểm BC
D. Trung điểm AD
Lời giải:
Gọi I là trung điểm BC.
Ta có; tam giác BCD vuông tại D có DI là đường trung tuyến ứng với cạnh huyền BC nên:
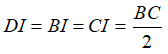
Tam giác ABC vuông tại A có AI là đường trung tuyến ứng với cạnh huyền BC nên:
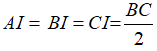
Từ (1) và (2) suy ra:
Do đó, I là tâm đường tròn ngoại tiếp tứ giác ABCD.
Đáp án cần chọn là:C
Câu 46: Cho hình thoi ABCD có AC = BD . Tìm tâm đường tròn ngoại tiếp hình thoi ABCD ?
A. Điểm A.
B. Giao điểm của AC và BD
C. Không có đường tròn ngoại tiếp tứ giác ABCD.
D. Trung điểm cạnh AB.
Lời giải:
Vì tứ giác ABCD là hình thoi có 2 đường chéo AC= BD nên tứ giác ABCD là hình vuông ( dấu hiệu nhận biết hình vuông)..
Gọi O là tâm hình vuông.
Theo tính chất hình vuông ta có:
Do đó, O là tâm đường tròn ngoại tiếp hình vuông ABCD.
Đáp án cần chọn là:B
Câu 47: Hình tròn tâm I, bán kính R = 4cm là gồm tất cả các điểm ........
A. có khoảng cách đến điểm I bằng 4cm
B. Có khoảng cách đến điểm I nhỏ hơn 4 cm.
C. Có khoảng cách đến điểm I lớn hơn 4 cm.
D. có khoảng cách đến điểm I nhỏ hơn hoặc bằng 4 cm.
Lời giải:
Hình tròn tâm I, bán kính R = 4cm là gồm tất cả các điểm có khoảng cách đến điểm I nhỏ hơn hoặc bằng 4 cm.
Đáp án cần chọn là:D
Câu 48: Cho tam giác ABC có các đường cao BD, CE. Chọn khẳng định đúng.
A. Bốn điểm B, E, D, C cùng nằm trên một đường tròn
B. Năm điểm A, B, E, D, C cùng nằm trên một đường tròn
C. Cả A, B, đều sai
D. Cả A, B đều đúng
Lời giải:
Gọi I là trung điểm BC.
Xét tam giác BEC vuông tại E có EI = IB = IC = 
Xét tam giác BDC vuông tại D có DI = IB = IC = 
Từ đó ta có ID = IE = IB = IC = 
Ta thấy IA > ID nên điểm A không thuộc đường tròn trên
Đáp án cần chọn là:A
Câu 49: Cho tam giác đều ABC cạnh bằng 3cm, các đường cao là BM và CN. Gọi O là trung điểm cạnh BC. Bốn điểm nào sau đây cùng thuộc một đường tròn
A. B, N, M, C
B. A, B, M, N
C. A, C, M, N
D. Cả A, B, C đều sai
Lời giải:
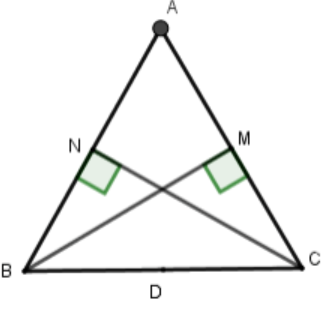
Đáp án cần chọn là:A
Câu 50: Cho hình vuông ABCD cạnh 4cm. Gọi M, N lần lượt là trung điểm của AB, BC. Gọi E là giao điểm của AM và DN. Bán kính của đường tròn đi qua bốn điểm A, D, E, M là?
A. R = 5cm
B. R = 10cm
C. R = cm
D. R = cm
Lời giải:
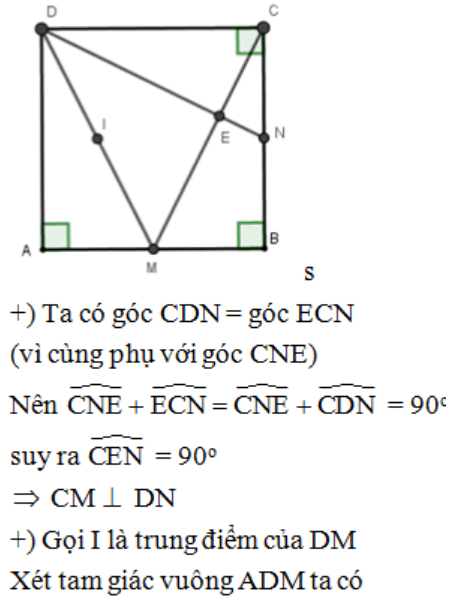

Đáp án cần chọn là:D
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.