Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 VBT Toán lớp 9 Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông trang 98,99,100,101,102 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:

VBT Toán lớp 9 Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông

Phần câu hỏi bài 4 trang 98 Vở bài tập toán 9 tập 1

Giải tam giác ABC biết ABC là tam giác vuông tại A và

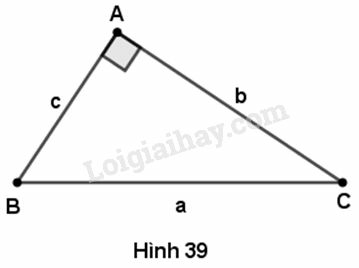
a) $b=10cm,\hat{C}={30}^o$

b) $c=10cm,\hat{C}={45}^o$

c) $a=20cm,\hat{B}={35}^o$

d) $c=21cm,b=18cm$

Phương pháp giải:

- Vận dụng kiến thức về định lí tổng ba góc trong một tam giác và hệ thức về cạnh và góc trong tam giác vuông để tìm góc và độ dài các cạnh còn thiếu. 

Trả lời:

a) Ta có : $\hat{B}={90}^o-\hat{C}={90}^o-{30}^o={60}^o.$

$c=b.\tan C=10\cdot {\displaystyle \frac{\sqrt{3}}{3}}\approx 5,77\left(cm\right).$

$a=b:\cos C=10:\cos {30}^o\approx 11,55\left(cm\right).$

b) Ta có :

$\hat{B}={90}^o-\hat{C}$$={90}^o-{45}^o={45}^o.$

Suy ra tam giác $ABC$ là tam giác vuông cân. Bởi vậy $b=c=10cm;$ $a=\sqrt{{10}^2+{10}^2}\approx 14,14\left(cm\right).$

c) Ta có : $\hat{C}={90}^o-\hat{B}$$={90}^o-{35}^o={55}^o;$

$b=a.\sin B=20.\sin {35}^o\approx 11,47\left(cm\right);$

$c=a.\cos B=20.\cos {35}^o=16,38\left(cm\right).$

d) Ta có

$\tan B={\displaystyle \frac{b}{c}}={\displaystyle \frac{18}{21}}\approx 086$$\Rightarrow \hat{B}\approx {40}^o{36}^{\prime };$

$\hat{C}={90}^o-\hat{B}$$\approx {90}^o-{40}^o{36}^{\prime }={49}^o{24}^{\prime };$

$a=\sqrt{b^2+c^2}=\sqrt{{18}^2+{21}^2}$$\approx 27,66\left(cm\right).$

Một cột đèn cao 7m có bóng trên mặt đất dài 4m. hãy tính góc mà tia sáng mặt trời tạo với mặt đất (góc  trong hình 40, làm tòn đến phút).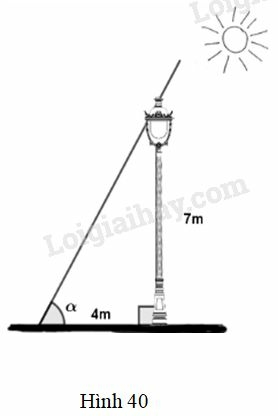

Phương pháp giải:

Vận dụng kiến thức $\tan \alpha ={\displaystyle \frac{\text{cạnh đối}}{\text{cạnh kề}}}$ rồi tìm giá trị của góc $\alpha .$

Trả lời:

Ta có $\tan \alpha ={\displaystyle \frac{7}{4}}=1,75.$

$\Rightarrow \alpha \approx {60}^o{15}^{\prime }.$

Cho tam giác ABC có $AB=11cm,\widehat{ABC}={38}^o,\widehat{ACB}={30}^o$. Gọi N là chân đường cao vuông góc kẻ từ A đến BC. Hãy tính AN và AC (làm tròn đến chữ số thập phân thứ hai).

Phương pháp giải:

Vận dụng kiến thức : Trong tam giác vuông, $\sin \alpha ={\displaystyle \frac{\text{cạnh đối}}{\text{cạnh huyền}}}$ để tìm độ dài của cạnh góc vuông hoặc cạnh huyền.

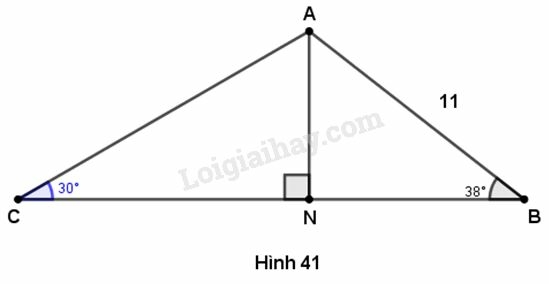
Trả lời:

Trong tam giác vuông $ANB,$ ta có : $\sin B={\displaystyle \frac{AN}{AB}}$ hay $\sin {38}^o={\displaystyle \frac{AN}{11}}$

Suy ra $AN=11.\sin {38}^o\approx 6,77\left(cm\right).$

Trong tam giác vuông $ANC,$ ta có : $\sin C={\displaystyle \frac{AN}{AC}}$ hay $\sin {30}^o\approx {\displaystyle \frac{6,77}{AC}}$

Suy ra $AC\approx {\displaystyle \frac{6,77}{\sin {30}^o}}=13,54\left(cm\right).$

Cho tam giác ABC, trong đó $BC=11cm,\widehat{ABC}={38}^o,\widehat{ACB}={30}^o$..Gọi N là chân đường cao vuông góc kẻ từ A đến cạnh BC. Hãy tính:

a) Đoạn AN

b) Cạnh AC

(Gợi ý: Kẻ BK vuông góc với AC) 

Phương pháp giải:

- Kẻ thêm đoạn $BK$ vuông góc với $AC$ để có tìm độ dài cạnh $AB.$

- Vận dụng các tỉ số lượng giác và hệ số về cạnh và góc trong tam giác vuông để tìm độ lớn cạnh $AN$ và $AC.$

Trả lời:

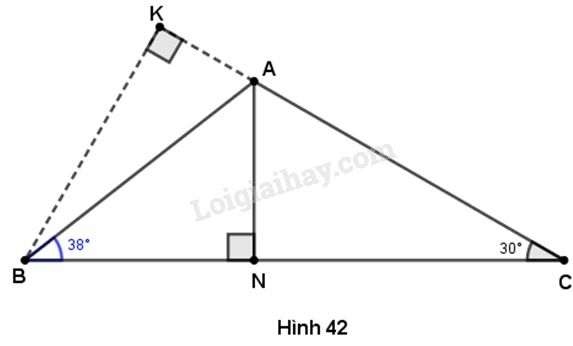
Kẻ $BK$ vuông góc với $AC\left(K\in AC\right).$ Ta có tam giác $BKC$ vuông tại $K.$ Do $\hat{C}={30}^o$ nên $\widehat{KBC}={60}^o.$ Từ đó :

$BK=BC\sin C=11\sin {30}^o$$={\displaystyle \frac{11}{2}}=5,5\left(cm\right).$

$\widehat{KBA}=\widehat{KBC}-\widehat{ABC}$$={60}^o-{38}^o={22}^o.$

Trong tam giác vuông $ABK,$ biết $BK=5,5cm$ và $\widehat{KBA}={22}^o,$ do đó $AB=BK:\cos \widehat{ABK}=55:\cos {22}^o$$\approx 5,932\left(cm\right).$

a) Trong tam giác vuông $ANB,$ ta có $AN=AB.\sin \widehat{ABC}$$\approx 5,932.\sin {38}^o\approx 3,652\left(cm\right).$

b) Trong tam giác vuông $ANC,$ ta có : $AC=AN:\sin \widehat{ACB}$$\approx 3,652:\sin {30}^o\approx 7,304\left(cm\right).$

Bài 32 trang 100 Vở bài tập toán 9 tập 1

Một con thuyền với vận tốc 2km/h vượt qua một khúc sông nước chảy mất mạnh mất 5 phút. Biết rằng đường đi của con thuyền tạo với bờ một góc 70^o. Từ đó đã có thể tính được chiều rộng của khúc sông chưa ? Nếu có thể, hãy tính kết quả (làm tròn đến mét).

Phương pháp giải:

- Vẽ hình biểu diễn đường đi của con thuyền, chiều rộng của khúc sông và góc tạo bởi đường đi của con thuyền và bờ.

- Vận dụng hệ thức về cạnh và góc trong tam giác vuông. 

Trả lời:

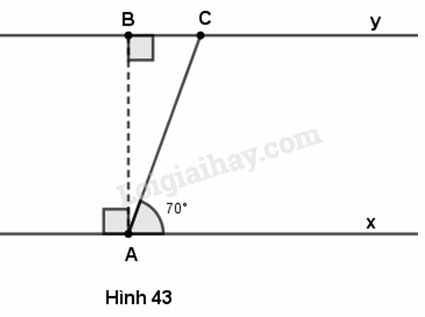
Ta có thể mô tả khúc sông và đường đi của con thuyền bởi hình 43, trong đó $AB$ là chiều rộng của khúc sông, $AC$ là đoạn đường đi của con thuyền.

Theo giả thiết, thuyền qua sông mất $5$ phút với vận tốc $2km/h(\approx 33m/$phút ), do đó :

$AC\approx 33.5=165\left(m\right).$

Trong tam giác vuông $ABC,$ đã biết $\hat{C}={70}^o\left(=\widehat{CAx}\right)$ và $AC\approx 165m$ nên độ dài cạnh $AB$ (chiều rộng của khúc sông) như sau :

$AB=AC.\sin C$$=165.\sin {70}^o\approx 155\left(m\right).$ 

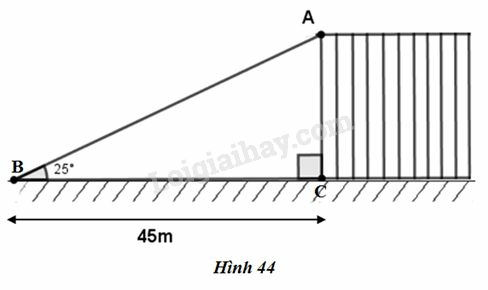
Để nhìn thấy đỉnh A của một vách đá dựng đứng, người ta đã đứng tại điểm B cách chân C của vách đá một khoảng 45m và nhìn lên một góc 25^o so với đường nằm ngang (góc nhìn lên này gọi là góc “nâng”). Tính độ cao của vách đá (làm tròn đến mét).

Phương pháp giải:

- Vận dụng kiến thức về hệ thức về cạnh và góc trong tam giác vuông để tìm độ dài cạnh AC