Toptailieu.vn giới thiệu Giải bài tập Toán 9 Bài 3:Bảng lượng giác chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Căn bậc hai lớp 9.
Giải bài tập Toán 9 Bài 3:Bảng lượng giác
Trả lời câu hỏi giữa bài:
Trả lời câu hỏi 1 trang 80 SGK Toán 9 Tập 1: Sử dụng bảng, tìm cot47o24’
Lời giải:
cot47o24’ = 0,9195
Trả lời câu hỏi 2 trang 80 SGK Toán 9 Tập 1: Sử dụng bảng, tìm tg82013′.
Trả lời câu hỏi 3 trang 81 SGK Toán 9 Tập 1: Sử dụng bảng tìm góc nhọn α, biết cotgα=3,006
Lời giải:
cotgα=3,006⇒α≈18o24′
Trả lời câu hỏi 4 trang 80 SGK Toán 9 Tập 1: Tìm góc nhọn α (làm tròn đến độ), biết cosα=0,5547
Lời giải:
cosα=0,5547 ⇒α≈560.
Bài tập trang 83-84 SGK Toán 9
Bài 18 trang 83 sgk Toán 9 - tập 1: Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm các tỉ số lượng giác sau (làm tròn tới chữ số thập phân thứ tư) :
a) sin40∘12′;
b) cos52∘54′;
c) tan63∘36′;
d) cot25∘18′.
Lời giải:
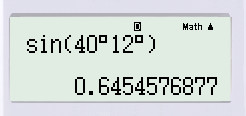
a) sin40∘12′≈0,6455;
b) cos52∘54′≈0,6032;

c) tan63∘36′≈2,0145;

d) cot25∘18′≈2,1155.
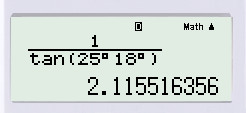
Nhận xét: Vì trong máy tính không có phím cotg nên để tìm cot25∘18′ ta phải tìm tan25∘18′ rồi lấy nghịch đảo của kết quả hay ta bấm luôn 1tan25∘18′ như trên.
Bài 19 trang 84 sgk Toán 9 - tập 1: Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm số đo của góc nhọn x (làm tròn đến phút), biết rằng:
a) sinx=0,2368;
b) cosx=0,6224;
c) tanx=2,154;
d) cotx=3,251.
Phương pháp giải:
a) sinα=m. Dùng máy tính lần lượt bấm các phím:

b) và c) làm tương tự.
d) ) Từ công thức tanα.cotα=1⇒tanα=1cotα. Biết cotα=n, tính được tanα. Dùng máy tính tính được góc α. Dùng máy tính bấm lần lượt các phím sau:

Lời giải:
a) sinx=0,2368⇒ x≈13∘42′;
Cách bấm máy:

b) cosx=0,6224⇒ x≈51∘31′;
Cách bấm máy:

c) tanx=2,154⇒ x≈65∘6′;
Cách bấm máy:
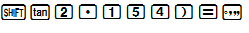
d) cotx=3,251⇒ x≈17∘6′.
Cách bấm máy:
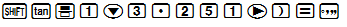
Bài 20 trang 84 sgk Toán 9 - tập 1: Dùng bảng lượng giác (có sử dụng phần hiệu chỉnh) hoặc máy tính bỏ túi, hãy tìm các tỉ số lượng giác sau (làm tròn đến chữ số thập phân thứ tư) :
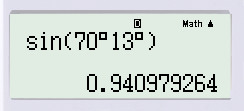
a) sin70∘13′;
b) cos25∘32′;
c) tan43∘10′;
d) cot32∘15′.
Phương pháp giải:
+) Thực hiện bấm máy tính và dùng quy tắc làm tròn số.
+) Sử dụng công thức tanα.cotα=1⇒cotα=1tanα.
Do đó để tính cotα, ta tính tanα sau đó nghịch đảo kết quả.
Lời giải:
a) sin70∘13′ ≈0,9410;
Cách bấm máy:
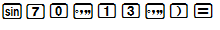
b) cos25∘32′ ≈0,9023;
Cách bấm máy:
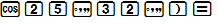

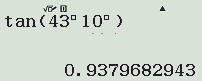
c) tan43∘10′ ≈0,9380;
Cách bấm máy:
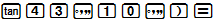
d) cot32∘15′ ≈1,5849.
Cách bấm máy:
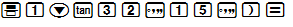

Bài 21 trang 84 sgk Toán 9 - tập 1: Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm góc nhọn x (làm tròn kết quả đến độ), biết rằng:
a) sinx=0,3495;
b) cosx=0,5427;
c) tanx=1,5142;
d) cotx=3,163.
Phương pháp giải:
a) b) c) Dùng máy tính bỏ túi
d) Sử dụng công thức tanα.cotα=1⇒tanα=1cotα.
Biết cotα tính được tanα từ đó tìm được góc α.
Lời giải:
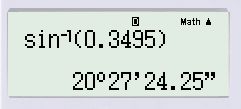
a) sinx=0,3495⇒x≈20∘;
Cách bấm máy:

b) cosx=0,5427⇒x≈57∘;
Cách bấm máy:

c) tanx=1,5142⇒x≈57∘;
Cách bấm máy:

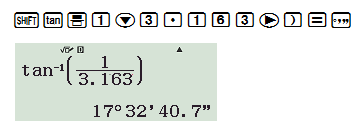
d) cotx=3,163⇒x≈18∘.
Cách bấm máy:
Bài 22 trang 84 sgk Toán 9 - tập 1: So sánh:
a) sin20∘ và sin70∘
b) cos25∘ và cos63∘15′
c) tan73∘20′ và tan45∘
d) cot2∘ và cot37∘40′
Phương pháp giải:
Nếu 0o<α , β<90o thì:
+) α<β⇒sinα<sinβ
+) α<β⇒cosα>cosβ.
+) α<β⇒tanα<tanβ.
+) α<β⇒cotα>cotβ.
Lời giải:
a) Vì 20∘<70∘ nên sin20∘<sin70∘ (góc tăng, sin tăng)
b) Vì 25∘<63∘ nên cos25∘>cos63∘15′ (góc tăng, cos giảm)
c) Vì 73∘20′>45∘ nên tan73∘20′>tan45∘ (góc tăng, tan tăng)
d) Vì 2∘<37∘40′ nên cot2∘>cot37∘40′ (góc tăng, cot giảm )
Chú ý sai lầm: Một số bạn từ 25∘<63∘15′ ở câu b suy ra cos25∘<cos63∘15′ là sai vì khi góc α tăng từ 0∘ đến 90∘ thì cosα giảm.
Bài 23 trang 84 sgk Toán 9 - tập 1: Tính:
a) sin25∘cos65∘
b) tan58∘−cot32∘
Phương pháp giải:
a) Dùng công thức hai góc phụ nhau: Nếu α+β=90o thì sinα=cosβ để đưa về cùng sin.
b) Dùng công thức hai góc phụ nhau: Nếu α+β=90o thì tanα=cotβ để đưa về cùng tan.
Lời giải:
a) Ta có: sin25∘cos65∘=sin25∘sin(90o−65o)=sin25∘sin25∘=1.
b) Ta có: tan58∘−cot32∘=tan58∘−tan(90o−32o)=tan58∘−tan58∘=0
Nhận xét: Cách giải như trên là dựa vào định lý: nếu hai góc phụ nhau thì sin của góc này bằng côsin của góc kia, tang của góc này bằng côtang của góc kia.
Bài 24 trang 84 sgk Toán 9 - tập 1: Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần:
a) sin78∘,cos14∘,sin47∘,cos87∘;
b) tan73∘,cot25∘,tan62∘,cot38∘.
Phương pháp giải:
a) +) Sử dụng công thức cosα=sin(90o−α)=sinβ để đưa hết về cùng là sin của một góc.
+) Nếu α<β⇒sinα<sinβ, với 0o<α , β<90o.
b) +) Sử dụng công thức cotα=tan(90o−α)=tanβ để đưa hết về cùng là tan của một góc.
+) Nếu α<β⇒tanα<tanβ, với 0o<α , β<90o.
Lời giải:
a) Ta có: cos14∘=sin(90o−14o)=sin76∘;
cos87∘=sin(90o−87o)=sin3∘.
Vì 3o<47o<76o<78o
⇒sin3∘<sin47∘<sin76∘<sin78∘
⇒cos87∘<sin47∘<cos14∘<sin78o.
b) Ta có: cot25∘=tan(90o−25o)=tan65∘;
cot38∘=tan(90o−38o)=tan52∘.
Vì 52o<62o<65o<73o
⇒tan52∘<tan62∘<tan65∘<tan73∘;
⇒cot38∘<tan62∘<cot25∘<tan73∘.
Bài 25 trang 84 sgk Toán 9 - tập 1: So sánh:
a) tan25o và sin25o.
b) cot32o và cos32o;
c) tan45o và cos45o;
d) cot60o và sin30o.
Phương pháp giải:
+) Sử dụng các công thức định nghĩa tỉ số lượng giác. Chú ý rằng 0<cosα, sinα<1 với 0o<α<90o.
+) Sử dụng công thức tỉ số lượng giác của hai góc phụ nhau: nếu α+β=90o thì:
sinα=cosβ; cosα=sinβ.
Lời giải:
a) Ta có tan25o=sin25ocos25o>sin25o ( do 0<cos250<1)
b) Ta có: cot32o=cos32osin32o>cos32o ( do 0<sin320<1)
c)
Cách 1:
Ta có tan450=1>√22=cos450
Cách 2:
Ta có tan45o=sin45ocos45o>sin45o ( do 0<cos450<1)
Mà sin45o=cos(90o−45o)=cos45o
Vậy tan45o>cos45o.
d) Cách 1:
Ta có cot600=√33>12=sin300
Cách 2:
Ta có: cot60o=cos60osin60o>cos60o ( do 0<sin600<1)
Mà cos60o=sin(90o−60o)=sin30o
Do đó cot60o>sin30o.
Chú ý:
Với các góc đặc biệt, ta có thể tính tỉ số lượng giác của chúng rồi so sánh
Lý thuyết Bài 3:Bảng lượng giác
1. Cấu tạo của bảng lượng giác
- Bảng sin và côsin (Bảng VIII)
- Bảng tang và côtang (Bảng IX)
- Bảng tang của các góc gần 90° (Bảng X)
Nhận xét:
Khi góc α tăng từ 0° đến 90° (0°<α < 90°) thì sinα và tgα tăng còn cosα và cotgα giảm.
2. Cách dùng bảng, dùng máy tính:
a) Tìm tỉ số lượng giác của một góc nhọn cho trước.
b) Tìm số đo của góc nhọn khi biết một tỷ số lượng giác của góc đó.