Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Các dạng toán về dây cung của đường tròn (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 9.

Phương pháp giải Các dạng toán về dây cung của đường tròn (50 bài tập minh họa)

I. Lý thuyết

1. Khái niệm dây của đường tròn

- Dây của đường tròn là đoạn thẳng nối hai điểm trên đường tròn.

- Đường kính cũng là một dây của đường tròn.

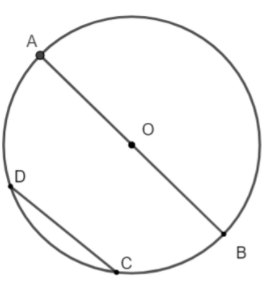
Xét hình vẽ trên

Ta nói CD và AB là hai dây của đường tròn

Đặc biệt dây AB còn là đường kính.

2. So sánh độ dài đường kính và dây

 Trong các dây của đường tròn, đường kính là dây lớn nhất.

3. Quan hệ vuông góc giữa đường kính và dây

- Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

- Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.

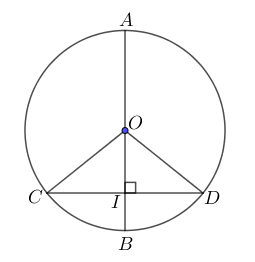
Cho đường tròn tâm O đường kính AB và dây CD không đi qua tâm

Nếu AB đi qua trung điểm I của CD thì AB$\perp$CD

Nếu AB $\perp$CD thì AB đi qua trung điểm I của CD.

4. Liên hệ giữa dây và khoảng cách từ tâm đến dây

- Trong một đường tròn

+ Hai dây bằng nhau thì cách đều tâm.

+ Hai dây cách đều tâm thì bằng nhau.

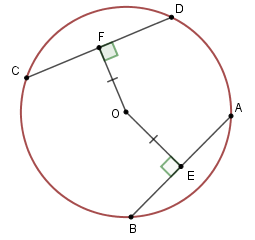
Dây AB = CD khi và chỉ khi khoảng cách từ O đến AB bằng khoảng cách từ O đến CD

Khoảng cách từ O đến AB và CD sẽ bằng nhau nếu dây AB = CD

- Trong hai dây của một đường tròn

+ Dây nào có độ dài lớn hơn thì dây đó gần tâm hơn.

+ Dây nào gần tâm hơn thì dây đó có độ dài lớn hơn.

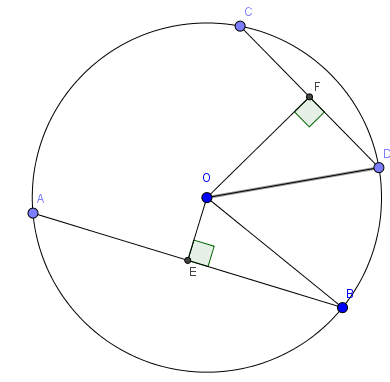
Xét hình vẽ:

Dây AB gần tâm hơn dây CD nên AB > CD.

II. Các dạng bài tập

Dạng 1: Tính độ dài đoạn thẳng, so sánh độ dài hai đoạn thẳng

Phương pháp giải:

Vận dụng những kiến thức đã học:

+ Quan hệ vuông góc giữa đường kính và dây

+ Dùng định lý Py – ta – go , hệ thức lượng trong tam giác vuông.

Ví dụ 1: Cho đường tròn (O; R) có dây AB và CD bằng nhau và vuông góc với nhau tại I (I khác O). Cho IA = 2cm, IB = 4cm. Tính khoảng cách từ tâm O đến mỗi dây và bán kính R.

Lời giải:

Ta có:

CD = AB = IA + IB = 2 + 4 = 6cm

Vẽ OG $\perp$AB tại G; OF$\perp$CD tại F

Vì OG $\perp$AB nên G là trung điểm của AB

Vì OF $\perp$CD nên F là trung điểm của CD

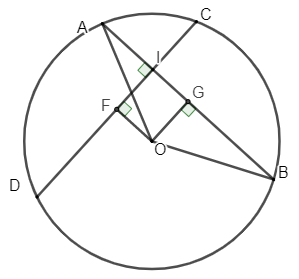
Vì G là trung điểm của AB nên AG = GB = 6 : 2 = 3cm

 $\Rightarrow$IG = AG – AI = 3 – 2 = 1cm

Xét tứ giác OGIF có

 $\widehat{FIG}=\widehat{IGO}=\widehat{OFI}=90°$

 $\Rightarrow$Tứ giác OGIF là hình chữ nhật (1)

Lại có AB = CD nên khoảng cách từ O đến AB bằng khoảng cách từ O đến CD

$\Rightarrow$ OG = OF (tính chất) (2)

Từ (1) và (2) $\Rightarrow$  Tứ giác OGIF là hình vuông

$\Rightarrow$ OG = OF = 1cm

Xét tam giác OAG vuông tại G ta có:

$A{O}^2=O{G}^2+A{G}^2$ (Định lý Py – ta – go)

$\iff A{O}^2=1^2+3^2$

$\iff A{O}^2=1+9$

$\iff A{O}^2=10$

$\iff AO=\sqrt{10}cm$

Vậy bán kính đường tròn là R = $\sqrt{10}cm$ .

Ví dụ 2: Cho AB và CD là hai dây khác đường kính của đường tròn (O; R). Gọi OE, OF theo thứ tự là khoảng cách từ O đến AB; CD. Chứng minh rằng: $O{E}^2+E{B}^2=O{F}^2+F{D}^2$ .

Lời giải:

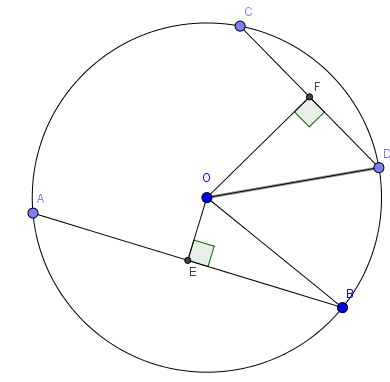
Xét tam giác vuông tại E ta có:

$O{E}^2+E{B}^2=O{B}^2=R^2$(Định lý Py – ta – go)   (1)

Xét tam giác vuông tại F ta có:

$O{F}^2+F{D}^2=O{D}^2=R^2$(Định lý Py – ta – go)   (2)

Từ (1) và (2)

$\Rightarrow O{E}^2+E{B}^2=O{F}^2+F{D}^2=R^2$ (điều phải chứng minh).

Ví dụ 3: Cho đường tròn tâm O, các dây AB và CD bằng nhau, đường thẳng AB và CD cắt nhau tại điểm E nằm bên ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Chứng minh rằng: EH = EK.

Lời giải:

Xét trong đường tròn (O):

Vì K là trung điểm của CD nên OK$\perp$ CD $\Rightarrow \widehat{OKE}=90°$

Vì H là trung điểm của AB nên OH$\perp$ AB $\Rightarrow \widehat{OHE}=90°$

Vì AB = CD nên OK = OH (tính chất)

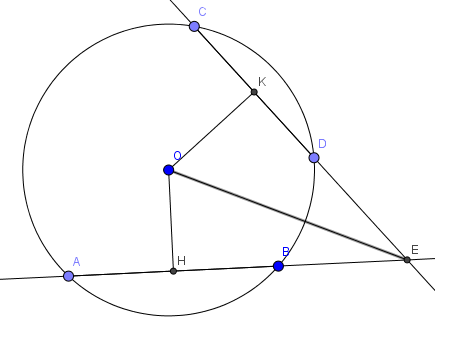
Xét $\Delta OKE$ và $\Delta OHE$ có:

OK = OH = (cmt)

$\widehat{OKE}=\widehat{OHE}=90°$

OE chung

Do đó  $\Delta OKE=\Delta OHE$ (cạnh huyền – cạnh góc vuông)

$\Rightarrow$ EH = EK.

Dạng 2: Chứng minh hai đoạn thẳng bằng nhau

Phương pháp giải: Sử dụng kiến thức

- Trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây ấy.

- Trong một đường tròn, đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây ấy.

- Trong một đường tròn:

+ Hai dây bằng nhau thì cách đều tâm.

+ Hai dây cách đều tâm thì bằng nhau.

Ví dụ 1: Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB. Kẻ AE và BG lần lượt vuông góc với CD tại E và G. Chứng minh CE = DG.

Lời giải:

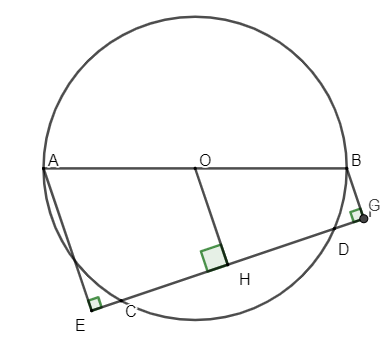
Gọi H là trung điểm của CD

$\Rightarrow$  OH $\perp$CD $\Rightarrow$  OH $\perp$EG

Vì $\left\{\begin{array}{l}BG\perp EG\\ AE\perp EG\end{array}\right.\Rightarrow AE\text{\hspace{0.17em}//\hspace{0.17em}}BG$

Xét tứ giác ABGE có:

AE // BG

$\Rightarrow$ Tứ giác ABGE là hình thang

Lại có OH $\perp$EG nên OH // AE // BG

Mà OH đi qua trung điểm O của AB nên OH đi qua trung điểm của EG

$\Rightarrow$ H là trung điểm của EG

$\Rightarrow$ HE = HG

Ta có:

$\left\{\begin{array}{l}HE=EC+CH\\ HG=DG+HD\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}EC=HE-CH\\ DG=HG-HD\end{array}\right.$

Mà HE = HG (cmt) ; CH = HD (H là trung điểm của CD)

Do vậy EC = DG.

Ví dụ 2: Cho đường tròn (O) đường kính AB. Kẻ hai dây AC và BD sao cho AC // BD. Chứng minh: AC = BD.

Lời giải:

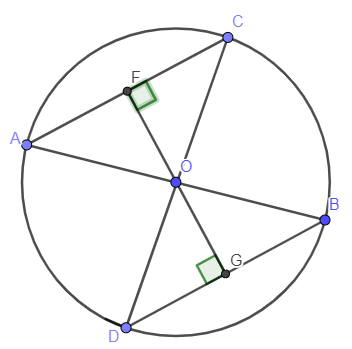
Gọi F là trung điểm của AC; G là trung điểm của BD

$\Rightarrow \left\{\begin{array}{l}O\text{}F\perp AC\\ OG\perp BD\end{array}\right.$

Mà AC // BD nên O, F, G thẳng hàng

Xét $\Delta AOF$ và $\Delta BOG$  có

OA = OB  (bán kính)

$\widehat{AO\text{}F}=\widehat{BOG}$ (hai góc đối đỉnh)

$\widehat{O\text{}FA}=\widehat{OGB}=90°$

Do đó $\Delta AO\text{}F$= $\Delta BOG$ ( cạnh huyền – góc nhọn)

$\Rightarrow$ AF = BG mà F là trung điểm của AC, G là trung điểm của BD

$\Rightarrow$ AC = BD.

Dạng 3: Liên hệ giữa dây và khoảng cách từ tâm tới dây

Phương pháp giải: Sử dụng kiến thức

Trong một đường tròn:

+ Đường kính là dây lớn nhất.

+ Hai dây bằng nhau thì cách đều tâm.

+ Hai dây cách đều tâm thì bằng nhau.

+ Dây nào có độ dài lớn hơn thì dây đó gần tâm hơn.

+ Dây nào gần tâm hơn thì có độ dài lớn hơn

Ví dụ 1: Cho tam giác ABC, các đường cao BH và CK.

a) Chứng minh bốn điểm B, H, C, K thuộc cùng một đường tròn.

b) BC > HK.

Lời giải:

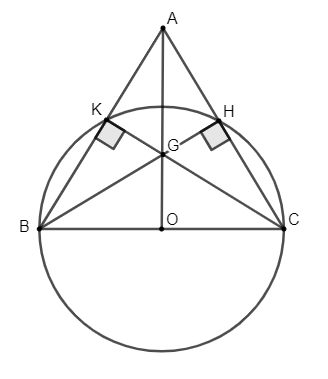
a) Gọi O là trung điểm của BC

Xét tam giác BKC vuông tại K, trung tuyến KO ta có:

$BO=OC=OK=\frac{1}{2}BC$ (tính chất đường trung tuyến ứng với cạnh huyền) (1)

Xét tam giác BHC vuông tại H, trung tuyến HO ta có:

$BO=OC=OH=\frac{1}{2}BC$ (tính chất đường trung tuyến ứng với cạnh huyền) (2)

Từ (1) và (2) $\Rightarrow BO=OC=OH=OK=\frac{1}{2}BC$

$\Rightarrow$ B, H, K, C cùng cách đều O

$\Rightarrow$ B, H, C, K thuộc đường tròn tâm O đường kính BC

b) Vì tâm O nằm trên BC và B, C là hai điểm thuộc đường tròn (O) nên BC là đường kính

Lại có H, K thuộc đường tròn (O) nên HK là dây của đường tròn

Tuy vậy tâm O không thuộc HK  nên HK < BC (trong các dây đường kính là dây dài nhất).

Ví dụ 2: Cho đường tròn (O; R) các dây cung AB; AC; AD (khác đường kính). Gọi M, N là hình chiếu của B lên AC; AD. Chứng minh MN < 2R.

Lời giải:

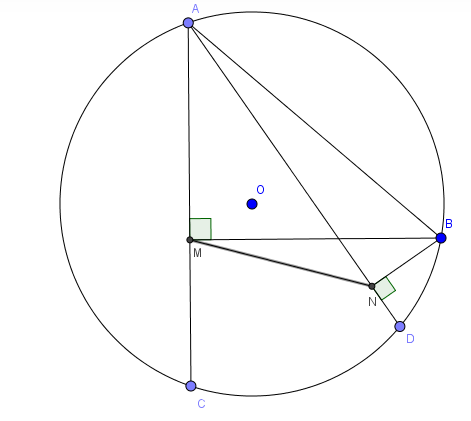
Xét tam giác AMB vuông tại M

$\Rightarrow$ A, M, B thuộc một đường tròn đường kính AB (1)

Xét tam giác ANB vuông tại N

$\Rightarrow$ A, N, B thuộc một đường tròn đường kính AB (2)

Từ (1) và (2) $\Rightarrow$  A, M, N, B cùng nằm trên một đường tròn với AB là đường kính.

Khi đó MN là dây

$\Rightarrow$ MN $\le$AB

Mà AB lại là dây của đường tròn (O)

$\Rightarrow$ AB < 2R

$\Rightarrow$ MN < 2R.

III. Bài tập vận dụng

Phần 1: Trắc nghiệm

Câu 1: Cho (O; 15cm) có dây AB = 24cm. Tính khoảng cách từ tâm O đến dây AB:

A. 12cm                B. 9cm                  C. 8cm                  D. 6cm

Câu 2: Cho các khẳng định sau:

i) Đường kính là dây dài nhất của đường tròn

ii) Trong một đường tròn, dây nào xa tâm hơn thì lớn hơn

iii) Đường tròn có vô số trục đối xứng

iv) Mỗi dây của đường tròn đều là trục đối xứng của đường tròn đó.

v) (O; 2cm) có nghĩa là đường tròn tâm O có đường kính là 2cm

Trong các khẳng định trên có bao nhiêu khẳng định đúng.

A. 2                      B. 3                      C. 4                      D. 5

Câu 3: Cho đường tròn (O; 10cm). Khi đó dây lớn nhất của đường tròn có độ dài là:

A. 5cm                  B. 10cm                         C. 15cm                         D. 20cm

Câu 4: Cho đường tròn có bán kính là 10cm. Một dây cung thuộc đường tròn. Số nào sau đây không thể là khoảng cách của đường tròn đến dây cung đó:

A. 5cm                  B. 11cm                C. 7cm                  D. 1cm

Phần 2: Tự luận

Bài 1: Cho đường tròn (O) và dây CD.  Từ O kẻ đường thẳng vuông góc với CD tại M cắt (O) tại H. Cho CD = 16cm và MH = 4cm. Tính bán kính đường tròn.

Bài 2: Cho đường tròn (O), đường kính AB; dây CD cắt AB tại M, cho MC = 4cm, MD = 12cm và $\widehat{BMD}=30°$ . Hãy tính:

a) Khoảng cách từ O đến CD.

b) Bán kính của O.

Bài 3: Cho tam giác ABC nhọn (AB < AC), M là trung điểm của BC, H là trực tâm của tam giác ABC. Lấy D đối xứng với H qua M.

a) Chứng minh tứ giác BHCD là hình bình hành.

b) Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. Chứng minh: $OM=\frac{1}{2}AH$ .

Bài 4: Cho nửa đường tròn đường kính AD. Trên nửa đường tròn lấy hai điểm B và C sao cho AB = BC và CD = 6cm. Tính bán kính đường tròn.

Bài 5: Cho (O; R) đường kính AB và dây cung DE. Tia DE cắt AB tại C. Biết $\widehat{DOE}=90°$ và OC = 3R. Tính

a) CD và CE theo R.

b) Chứng minh: CD.CE = CA.CB.

Bài 6: Cho tam giác ABC đường cao BD và CE cắt nhau tại H. Lấy I là trung điểm của BC.

a) Gọi K là điểm đối xứng của H qua I. Chứng minh tứ giác BHCK là hình bình hành.

b) Xác định O là tâm đường tròn qua các điểm A, B, K, C.

Bài 7: Cho điểm A nằm trên đường tròn (O) có CB là đường kính và AB < AC. Vẽ dây AD vuông góc với BC tại H. Chứng minh:

a) Tam giác ABC vuông tại A.

b) H là trung điểm của AD, AC = CD và BC là tia phân giác góc ABD.

Đáp án trắc nghiệm

Câu 1: B

Câu 2: A

Câu 3: D

Câu 4: B