Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Vị trí tương đối của hai đường tròn (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 9.
Phương pháp giải Vị trí tương đối của hai đường tròn (50 bài tập minh họa)
I. Lý thuyết
1. Vị trí tương đối của hai đường tròn
- Hai đường tròn cắt nhau là hai đường tròn có hai điểm chung.
- Hai đường tròn tiếp xúc nhau là hai đường tròn có một điểm chung.
- Hai đường tròn không cắt nhau là hai đường tròn không có điểm chung.
2. Khái niệm đường nối tâm
Đường nối tâm (đường thẳng đi qua tâm 2 đường tròn) là trục đối xứng của hình tạo bởi hai đường tròn.
Đoạn nối tâm là đoạn thẳng nối hai tâm của đường tròn với mỗi tâm là một đầu mút.
3. Tính chất đường nối tâm
- Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.
- Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây chung.
4. Liên hệ giữa vị trí của hai đường tròn với đoạn nối tâm d và các bán kính R và r
Cho hai đường tròn (O; R) và (O’; r) với R > r
- Hai đường tròn cắt nhau thì R – r < d < R + r và hai đường tròn (O) và (O’) có 2 điểm chung
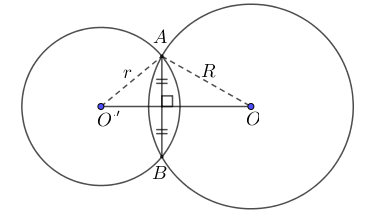
Điểm chung của (O) và (O’) là A và B.
- Hai đường tròn tiếp xúc nhau (O) và (O’) có một điểm chung:
+ Tiếp xúc trong: d = R – r
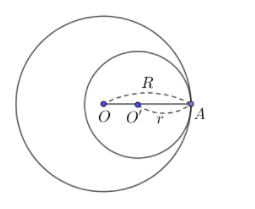
Điểm chung của O và O’ là A và O’ nằm giữa O và A
+ Tiếp xúc ngoài: d = R + r
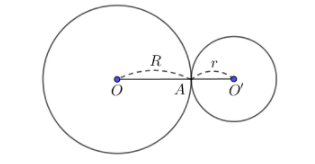
(O) và (O’) có một điểm chung là A và A nằm giữa O và O’.
- Hai đường tròn không giao nhau (O) và (O’) không có điểm chung:
+ (O) và (O’) nằm ngoài nhau: d > R + r
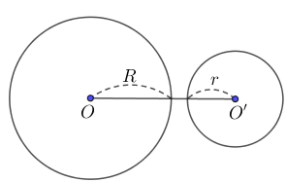
+ (O) đựng (O’): d < R – r
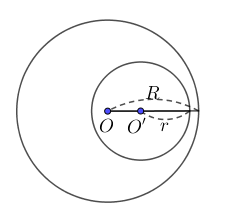
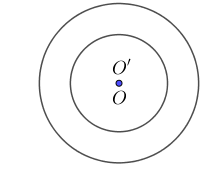
+ (O) và (O’) đồng tâm: d = 0
II. Một số dạng bài tập và phương pháp giải
Dạng 1: Các bài toán liên quan đến đường tròn tiếp xúc nhau
Phương pháp giải: Áp dụng các kiến thức về vị trí tương đối của hai đường tròn liên quan đến trường hợp hai đường tròn tiếp xúc nhau.
Cho hai đường tròn (O; R) và (O’; r) với R > r
+ Hai đường tròn tiếp xúc nhau (O) và (O’) có một điểm chung:
+ Tiếp xúc trong: d = R – r
+ Tiếp xúc ngoài: d = R + r
Ví dụ 1: Cho đường tròn (O) bán kính R. Lấy điểm A tùy ý trên (O). Vẽ đường tròn đường kính AO. Xác định vị trí tương đối của hai đường tròn.
Lời giải:
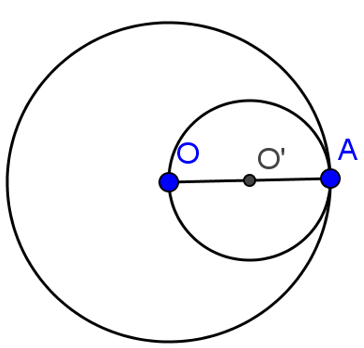
Gọi O’ là tâm của đường tròn đường kính OA. Ta có O’ là trung điểm của OA và bán kính đường tròn (O’) là
Đoạn nối tâm O, O’ là OO’ = =
Gọi r là bán kinh của (O’) ta có:
R – r = OA - = R - = nên (O) và (O’) tiếp xúc trong tại A.
Ví dụ 2: Cho đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC với B thuộc (O) và C thuộc (O’). Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC ở I.
a) Chứng minh .
b) Vẽ đường kính BOD và CO’E. Chứng minh các bộ ba điểm B, A, E và A, C, D thẳng hàng.
Lời giải:
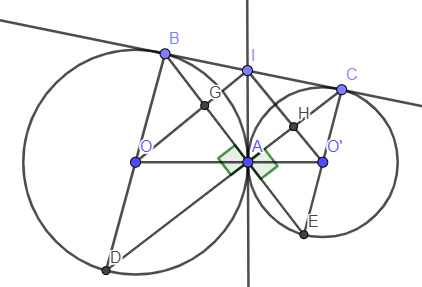
a) Gọi giao điểm của OI với AB là G
Gọi giao điểm của IO’ với AC là H
Vì BI và IA là hai tiếp tuyến của đường tròn (O) và chúng cắt nhau tại I nên .
Xét tam giác BIA ta có : IA = IB (tính chất hai tiếp tuyến IA, IB của (O) cắt nhau)
tam giác BIA cân tại I
IG là đường phân giác cũng là đường cao của tam giác BIA
Vì CI và IA là hai tiếp tuyến của đường tròn (O’) và chúng cắt nhau tại I nên .
Xét tam giác CIA có: IC = IA (tính chất hai tiếp tuyến IC và IA của (O’) cắt nhau)
tam giác CIA cân tại I.
IH là đường phân giác cũng là đường cao của tam giác CIA.
Ta lại có:
Mà và nên ta có:
Xét tứ giác AHIG có:
Do đó tứ giác AHIG là hình chữ nhật
hay (điều phải chứng minh).
b) Ta có: BD là đường kính của đường tròn (O) và A, B, D thuộc đường tròn (O) nên tam giác ABD là tam giác vuông
CE là đường kính của đường tròn (O’) và A, C, E thuộc đường tròn (O’) nên tam giác ACE là tam giác vuông.
Ta có: và
A, C, D thẳng hàng
Lại có:
và
A, E, B thẳng hàng.
Ví dụ 3: Cho hai đường tròn (O; R) và (O’; r) tiếp xúc ngoài với nhau tại A. Vẽ tiếp tuyến chung ngoài BC với B thuộc (O) và C thuộc (O’). Đường vuông góc với OO’ kẻ từ A cắt BC tại M.
a) Tính AM theo r và R.
b) Tính diện tích tứ giác BCO’O theo R và r.
Lời giải:
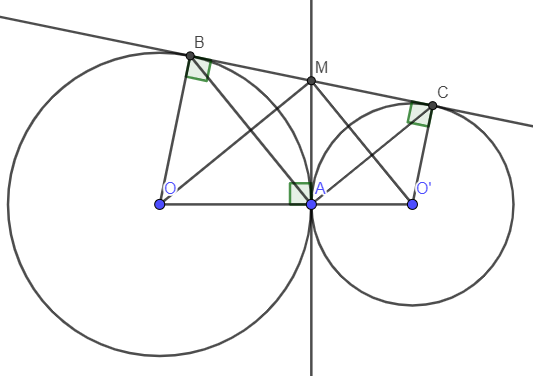
a) MA vuông góc với OO’ nên MA vuông góc với OA MA là tiếp tuyến của (O) tại A
MA vuông góc với OO’ nên MA vuông góc với O’A MA là tiếp tuyến của (O’) tại A
Vì MA và BM là hai tiếp tuyến cắt nhau nên OM là tia phân giác góc (tính chất hai tiếp tuyến cắt nhau)
Vì MA và CM là hai tiếp tuyến cắt nhau nên O’M là tia phân giác góc (tính chất hai tiếp tuyến cắt nhau)
Ta có:
Xét tam giác OMO’ vuông tại M, đường cao MA ta có:
(hệ thứ lượng trong tam giác vuông)
.
b) Xét và ta có:
(chứng minh trên)
OM chung
BM = AM (tính chất hai tiếp tuyến cắt nhau)
Do đó = (c – g – c)
Xét tam giác và ta có:
(chứng minh trên)
MO’ chung
AM = CM (tính chất hai tiếp tuyến cắt nhau)
Do đó = (c – g – c)
Diện tích tam giác AOM là
S = (đơn vị diện tích)
Diện tích tam giác AMO’ là
(đơn vị diện tích)
Ta có:
(do và )
(đơn vị diện tích).
Dạng 2: Các bài toán liên quan đến hai đường tròn cắt nhau
Phương pháp giải: Áp dụng các kiến thức liên quan đến hai đường tròn cắt nhau.
Cho hai đường tròn (O; R) và (O’; r) với R > r
- Hai đường tròn cắt nhau thì R – r < d < R + r và hai đường tròn (O) và (O’) có 2 điểm chung.
Ví dụ 1: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Một cát tuyến qua A cắt (O) ở M và cắt (O’) ở N, A nằm giữa M và N. Từ A vẽ đường kính AOC và AO’D.
Tứ giác CMND là hình gì?
Lời giải:
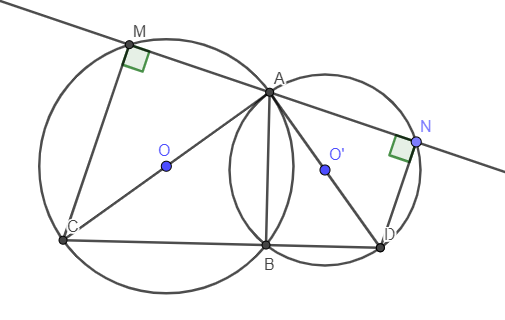
Vì A, C, M cùng thuộc đường tròn (O) và AC là đường kính nên tam giác AMC vuông tại M
MC MA (1)
Vì A, N, D cùng thuộc đường tròn (O’) và AD là đường kính nên tam giác AND vuông tại N
AN ND (2)
Từ (1) và (2)
Vì CM // DN nên tứ giác CMND là hình thang
Lại có nên tứ giác CMND là hình thang vuông.
Ví dụ 2: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B trong đó OA là tiếp tuyến của (O’). Tính độ dài dây cung AB biết OA = 20cm và O’A = 15cm.
Lời giải:
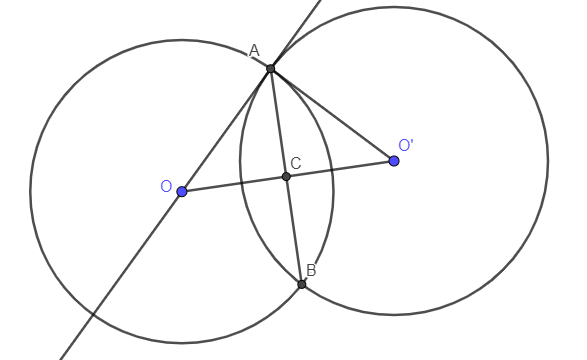
OO’ là đường nối hai tâm của hai đường tròn cắt nhau nên OO’ là đường trung trực của AB
OO’ đi qua trung điểm của AB và OO’ vuông góc với AB
Gọi giao điểm của OO’ và AB là C nên C là trung điểm của AB
Vì OA là tiếp tuyến của (O’) OA O’A
Xét tam giác OAO’ vuông tại A ta có:
(Định lý Py – ta – go)
Vì AC OO’ nên áp dụng hệ thức lượng trong tam giác vuông AOO’ ta có:
OA.O’A = AC.OO’
20.15 = AC.25
AC = 12cm
Ta có AB = 2AC (do C là trung điểm của AB)
AB = 12.2 = 24cm.
Dạng 3: Các bài toàn liên quan đến hai đường tròn không cắt nhau
Phương pháp giải: Áp dụng kiến thức hai đường tròn không cắt nhau.
- Hai đường tròn không giao nhau (O) và (O’) không có điểm chung:
+ (O) và (O’) nằm ngoài nhau: d > R + r
+ (O) đựng (O’): d < R – r
+ (O) và (O’) đồng tâm: d = 0
Ví dụ 1: Cho hai đường tròn đồng tâm O. Biết BC là đường kính của đường tròn lớn và có độ dài bằng 12cm. Dây CD của đường tròn lớn đồng thời là tiếp tuyến của đường tròn nhỏ và . Hãy tính bán kính đường tròn nhỏ.
Lời giải:
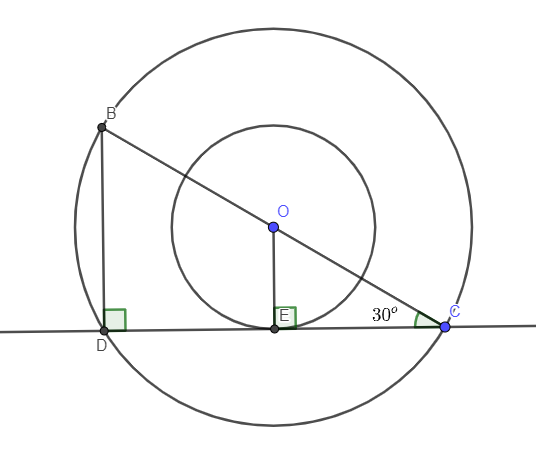
Vì CD là tiếp tuyến của đường tròn nhỏ (O) nên CD vuông góc với bán kính đi qua tiếp điểm. Gọi điểm tiếp xúc là E OE CD tại E.
Vì BC là đường kính đường tròn lớn (O) nên OC = BC : 2 = 12 : 2 = 6cm
Xét tam giác OEC vuông tại E ta có:
Vậy bán kính đường tròn nhỏ (O) là 3cm.
Ví dụ 2: Cho hai đường tròn (O; 6cm) và đường tròn (O’; 2cm) nằm ngoài nhau. Gọi AB là tiếp tuyến chung ngoài, CD là tiếp tuyến chung trong của hai đường tròn (A và C thuộc (O); B và D thuộc (O’)). Biết AB = 2CD, tính độ dài đoạn nối tâm OO’.
Lời giải:
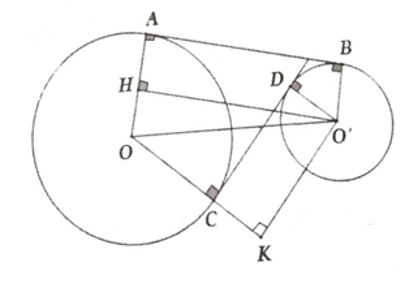
Kẻ O’H vuông góc với OA tại H và O’K vuông góc với OC tại K
Vì AB là tiếp tuyến chung ngoài của (O) và (O’) nên ta có:
OA AB và O’B AB
Xét tứ giác AHO’B có:
tứ giác AHO’B là hình chữ nhật
AH = O’B = 2cm OH = OA – AH = 6 – 2 = 4cm
Vì CD là tiếp tuyến chung trong của (O) và (O’) nên ta có:
O’D CD và OC CD
Xét tứ giác O’DCK có
O’DCK là hình chữ nhật
CK = O’D = 2cm OK = OC + CK = 2 + 6 = 8cm.
Đặt CD = x (với x > 0) AB = 2x và O’K = x (do O’DCK là hình chữ nhật)
Xét tam giác vuông OO’K có:
(Định lý Py – ta – go)
(1)
Ta có AB = HO’ = 2x (do ABO’H là hình chữ nhật)
Xét tam giác vuông OO’H ta có:
(Định lý Py – ta – go)
(2)
Từ (1) và (2) ta có:
.
III. Bài tập vận dụng
Bài 1: Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài tại A vẽ tiếp tuyến chung ngoài tiếp xúc (O) và (O’) lần lượt tại B và C. Tiếp tuyến chung trong cắt BC ở I. Gọi E, F theo thứ tự là giao điểm của IO với AB và của IO’ với AC.
a) Chứng minh A, E, I, F thuộc cùng một đường tròn. Xác định tâm K và bán kính.
b) Chứng minh IE.IO + IF.IO’ = .
c) Gọi P là trung điểm của OA. Chứng minh PE tiếp xúc với (K).
Bài 2: Cho hai đường tròn (O; R) và (O’; r) ở ngoài nhau. Gọi MN là tiếp tuyến chung ngoài, EF là tiếp tuyến chung trong (M và E thuộc (O), N và F thuộc (O’)). Tính bán kính đường tròn (O) và (O’) trong các trường hợp sau
a) OO’ = 10cm; MN = 8cm; EF = 6cm.
b) OO’ = 13cm; MN = 12cm; EF = 3cm.
Bài 3: Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A và B. Gọi M là trung điểm của OO’. Đường thẳng qua A cắt các đường tròn(O) và (O’)lần lượt ở C và D. Với CD vuông góc với MA. Chứng minh AC = AD.
Bài 4: Cho góc vuông xOy. Lấy các điểm I và K lần lượt nằm trên các tia Ox và Oy. Đường tròn (I; OK) cắt tia Ox tại M (I nằm giữa O và M), đường tròn (K; OI) cắt tia Oy tại N (K nằm giữa O và N).
a) Chứng minh (I) và (K) luôn cắt nhau.
b) Tiếp tuyến tại M của (I), tiếp tuyến tại N của (K) cắt nhau tại C. Chứng minh tứ giác OMCN là hình vuông.
Bài 5: Cho (O; R) và một điểm A nằm trên (O). Trên đoạn OA lấy điểm B sao cho OB = OA.
a) Chứng minh đường tròn đường kính AB tiếp xúc với (O).
b) Đường tròn (O; R’) với R R’ cắt đường tròn đường kính AB tại C. Tia AC cắt hai đường tròn đồng tâm tại D và E với D nằm giữa C và E.
Chứng minh AC = CD = DE.
Bài 6: Cho hai đường tròn (O;R) và (O’; r) tiếp xúc ngoài với nhau tại A. Vẽ tiếp tuyến chung ngoài BC với B thuộc (O) và C thuộc (O’). Đường vuông góc với OO’ kẻ từ A cắt BC tại M.
a) Tính diện tích tam giác BAC theo R và r.
b) Gọi I là trung điểm của OO’. Chứng minh rằng BC là tiếp tuyến của đường tròn (I; IM).
Bài 7: Cho đường tròn (O) đường kính AB và C là điểm nằm giữa A và O. Vẽ đường tròn (I) đường kính CB.
a) Xét vị trí tương đối của (O) và (I).
b) Xét dây DE của (O) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì?
c) Gọi K là giao điểm của đoạn thẳng DB và (I). Chứng minh ba điểm E, C, K thẳng hàng.
d) Chứng minh HK là tiếp tuyến của I.
Bài 8: Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A và B. Gọi M là trung điểm của OO’. Đường thẳng qua A cắt các đường tròn (O) và (O’) lần lượt ở C và D. Khi CD đi qua A và không vuông góc với MA
a) Vẽ đường kính AE của (O), AE cắt (O’) ở H. Vẽ đường kính AF của (O’), AF cắt (O) ở G. Chứng minh AB, EG, FH đồng quy.
b) Tìm vị trí của CD để đoạn CD có độ dài lớn nhất.
Bài 9: Cho hai đường tròn đồng tâm O, bán kính lần lượt là R và r, dây MN của đường tròn lớn cắt đường tròn nhỏ tại A và B. Gọi BC là đường kính của đường tròn nhỏ. Tính theo R và r giá trị biểu thức .
Bài 10: Cho hai đường tròn (O) và (O’) ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và CD (A, C thuộc (O), B và D thuộc (O’)). Tiếp tuyến chung MN cắt AB và CD theo thứ tự tại E và F (M thuộc (O), N thuộc (O’)). Chứng minh:
a) AB = EF
b) EM = FN.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.