Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Vị trí tương đối của đường thẳng và đường tròn (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 9.
Phương pháp giải Vị trí tương đối của đường thẳng và đường tròn (50 bài tập minh họa)
I. Lý thuyết
Cho đường thẳng và đường tròn (O; R). Gọi OH là khoảng cách từ tâm O đến đường thẳng .
+ Nếu OH > R thì không cắt (O) (không có điểm chung).
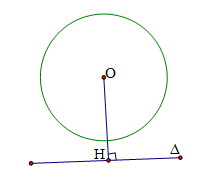
+ Nếu OH = R thì và (O) tiếp xúc nhau hay đường tròn (O) và đường thẳng ∆ có một điểm chung là H.
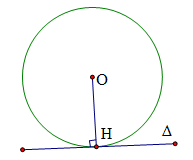
Khi đó là tiếp tuyến của đường tròn (O), H là tiếp điểm.
+ Nếu OH < R thì và (O) cắt nhau hay đường thẳng ∆ và đường tròn (O) có hai điểm chung là A và B.
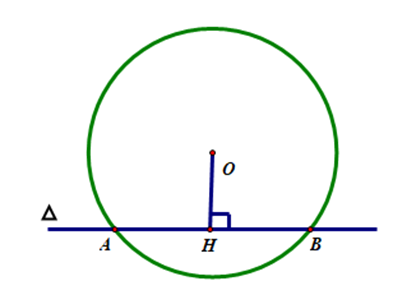
Khi đó là cát tuyến của đường tròn.
II. Các ví dụ
Ví dụ 1: Cho điểm A(1; 3). Hãy xác định vị trí tương đối của đường tròn (A; 2) với hai trục Ox; Oy.
Lời giải:
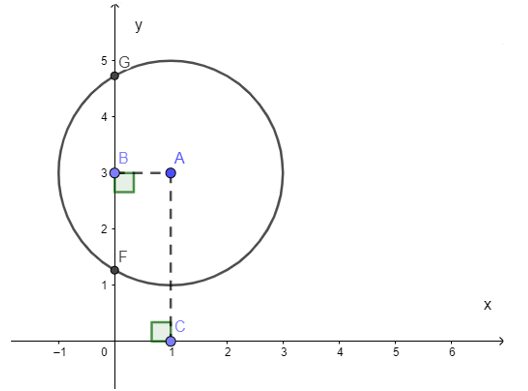
Vẽ AB Oy tại B AB = 1
Vẽ ACOx tại C AC = 3
Vì AB < R (1 < 2) nên đường tròn (A; 2) cắt trục Oy tại hai điểm F và G như hình vẽ hay (A; 1) cắt Oy.
Vì AC > R (3 > 2) nên đường tròn (A; 2) không cắt trục Ox hay (A) và Ox không giao nhau.
Ví dụ 2: Điền vào chỗ chấm
a) Đường thẳng tiếp xúc với đường tròn khi số giao điểm của đường thẳng và đường tròn là…
b) Đường thẳng không cắt đường tròn khi khoảng cách từ tâm đường tròn đến đường thẳng…
c) Đường tròn (O; 3cm), khoảng cách từ tâm O đến tiếp tuyến của đường tròn là…
d) Khoảng cách từ tâm của đường tròn đến đường thẳng nhỏ hơn bán kính của đường tròn thì đường thẳng và đường tròn ở vị trí…
Lời giải:
a) Đường thẳng tiếp xúc với đường tròn khi số giao điểm của đường thẳng và đường tròn là một.
b) Đường thẳng không cắt đường tròn khi khoảng cách từ tâm đường tròn đến đường thẳng lớn hơn bán kính của đường tròn.
c) Đường tròn (O; 3cm), khoảng cách từ tâm O đến tiếp tuyến của đường tròn là 3cm.
d) Khoảng cách từ tâm của đường tròn đến đường thẳng nhỏ hơn bán kính của đường tròn thì đường thẳng và đường tròn ở vị trí cắt nhau.
Ví dụ 3: Cho đường tròn (O; R) đường kính AB. Trên tia đối tia AB lấy điểm C. Từ C kẻ tiếp tuyến CD với (O), D là tiếp điểm. Kẻ DH AB tại H.
Chứng minh: CH.CO = CA.CB.
Lời giải:
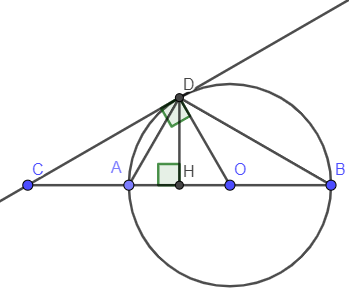
Vì CD là tiếp tuyến của đường tròn (O) với D là tiếp điểm nên OD CD tại D. Do đó tam giác COD là tam giác vuông tại D.
Lại có DH AB tại H nên DH CO tại H
Xét tam giác CDO vuông tại D, đường cao DH ta có:
(Hệ thức lượng trong tam giác vuông). (1)
Xét tam giác BOD có:
OB = OD = R
Do đó tam giác BOD cân tại O
(tính chất tam giác cân). (2)
Vì ABD có ba đỉnh cùng nằm trên một đường tròn (O) và AB là đường kính nên tam giác ABD vuông tại D.
(3)
Ta lại có:
(4)
Từ (3) và (4) (5)
Từ (2) và (5)
Xét tam giác CDA và tam giác CBD có:
chung
(chứng minh trên)
Do đó: (g – g) (sai kí hiệu đồng dạng)
(hai cặp cạnh tương ứng)
(6)
Từ (1) và (6) hay CA.CB = CH.CO.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.