Phương pháp giải Bài tập về góc nội tiếp (50 bài tập minh họa)

Bạn cần đăng nhập để báo cáo vi phạm tài liệu

Phương pháp giải Bài tập về góc nội tiếp (50 bài tập minh họa)

Ngọc Nguyễn Ngày: 15-07-2023 Lớp 9

293

Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Bài tập về góc nội tiếp (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 9.

Phương pháp giải Bài tập về góc nội tiếp (50 bài tập minh họa)

I. Lý thuyết

1. Định nghĩa góc nội tiếp

- Góc có đỉnh nằm trên đường tròn và hai cạnh là hai dây cung của đường tròn là góc nội tiếp.

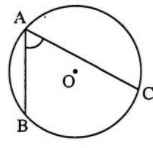
Phương pháp giải Bài tập về góc nội tiếp (50 bài tập minh họa) (ảnh 1)

Góc $\hat{B A C}$ có đỉnh A nằm trên đường tròn (O) và AB, AC là hai cạnh của góc cũng là hai dây của đường tròn. Do vậy $\hat{B A C}$ là góc nội tiếp của đường tròn (O).

2. Định lý

- Trong một đường tròn, số đo góc nội tiếp bằng một nửa số đo cung bị chắn.

3. Hệ quả

Trong một đường tròn

- Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

- Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

- Góc nội tiếp (có số đo nhỏ hơn hoặc bằng $90 °$ ) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.

- Góc nội tiếp chắn nửa đường tròn là góc vuông.

II. Các dạng bài tập

Dạng 1: Chứng minh hai góc bằng nhau, đoạn thẳng bằng nhau, tam giác đồng dạng

Phương pháp giải: Dùng hệ quả trong phần tóm tắt lí thuyết để chứng minh hai góc bằng nhau, hai đoạn thẳng bằng nhau.

Ví dụ 1: Cho tam giác ABC có ba góc nhọn đường cao AH và nội tiếp đường tròn (O). Vẽ đường kính AM.

a) Tính $\hat{A C M}$ .

b) Chứng minh $\hat{B A H} = \hat{O C A}$ .

Lời giải:

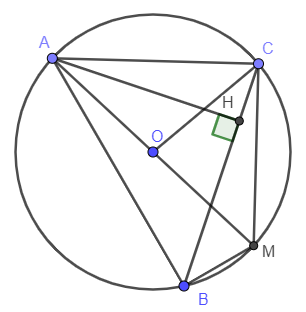
Bài tập về góc nội tiếp và cách giải – Toán lớp 9 (ảnh 1)

a) Ta có:

$\hat{A C M}$ có đỉnh C nằm trên đường tròn (O)

AC và BC là dây của đường tròn (O)

Do đó $\hat{A C M}$ là góc nội tiếp của đường tròn (O)

Mặt khác AM là đường kính nên $\hat{A C M}$ là góc nội tiếp chắn nữa đường tròn

$\Rightarrow \hat{A C M} = 90 °$ (do góc nội tiếp chắn nửa đường tròn là góc vuông).

b) $\hat{A B C}$ có đỉnh B nằm trên đường tròn (O) và BA, BC là hai dây của đường tròn

Do đó $\hat{A B C}$ là góc nội tiếp của đường tròn (O) chắn $\overset{⏜}{A C}$ .

Đặt góc $\hat{A B C} = x (0 < x < 90 °)$

Xét tam giác AHB vuông tại H có:

$\hat{B A H} + \hat{A B H} + \hat{A H B} = 180 °$ (định lý tổng ba góc trong một tam giác)

$\Leftrightarrow \hat{B A H} + x + 90 ° = 180 °$

$\Leftrightarrow \hat{B A H} = 180 ° - 90 ° - x$

$\Leftrightarrow \hat{B A H} = 90 ° - x$ (1)

Lại có $\hat{A O C}$ là góc ở tâm chắn cung $\overset{⏜}{A C}$ và $\hat{A B C}$ là góc nội tiếp chắn cung $\overset{⏜}{A C}$

$\Rightarrow \hat{A O C} = 2. \hat{A B C} = 2 x$

Xét tam giác OAC có:

OA = OC

=> tam giác OAC cân tại O

$\Rightarrow \hat{O A C} = \hat{O C A}$

Ta có:

$\hat{O A C} + \hat{O C A} + \hat{A O C} = 180 °$ (định lí tổng ba góc trong một tam giác).

$\Leftrightarrow 2 \hat{O C A} + 2 x = 180 °$

$\Leftrightarrow 2 (\hat{O C A} + x) = 180 °$

$\Leftrightarrow \hat{O C A} + x = 180 ° : 2$

$\Leftrightarrow \hat{O C A} + x = 90 °$

$\Leftrightarrow \hat{O C A} = 90 ° - x$ (2)

Từ (1) và (2) $\Rightarrow \hat{O C A} = \hat{B A H}$

Ví dụ 2: Cho đường tròn (O) và điểm I không nằm trên đường (O). Qua điểm I nằm ngoài đường tròn ta vẽ các dây cung AB và CD sao cho A nằm giữa B và I; C nằm giữa I và D.

a) So sánh các cặp góc $\hat{A C I}$ và $\hat{A B D}$ ; $\hat{C A I}$ và $\hat{C D B}$ .

b) Chứng minh tam giác IAC đồng dạng với tam giác IDB.

c) Chứng minh IA.IB = IC.ID.

Lời giải:

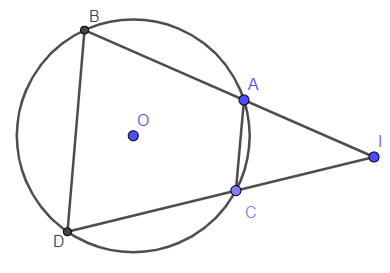
Bài tập về góc nội tiếp và cách giải – Toán lớp 9 (ảnh 1)

a) Ta có:

$\hat{A B D}$ là góc nội tiếp đường tròn (O) chắn $\overset{⏜}{A D}$ nhỏ.

$\Rightarrow \hat{A B D} = \frac{1}{2}$ sđ $\overset{⏜}{A D}$ nhỏ (định lí) (1)

Lại có: $\hat{A C D}$ là góc nội tiếp đường tròn (O) chắn $\overset{⏜}{A D}$ lớn.

$\Rightarrow \hat{A C D} = \frac{1}{2}$ sđ $\overset{⏜}{A D}$ lớn (định lí) (2)

Ta có:

sđ $\overset{⏜}{A D}$ nhỏ + sđ $\overset{⏜}{A D}$ lớn $= 360 °$

=> $\frac{1}{2}$ sđ $\overset{⏜}{A D}$ nhỏ + $\frac{1}{2}$ sđ $\overset{⏜}{A D}$ $= 180 °$ (3)

Từ (1); (2); (3) $\Rightarrow \hat{A C D} + \hat{A B D} = 180 °$ (4)

Ta có $\hat{A C D} + \hat{A C I} = 180 °$ (do hai góc kề bù) (5)

Từ (4) và (5) $\Rightarrow \hat{A B D} = \hat{A C I}$ (hai góc cùng bù với góc $\hat{A C D}$ ).

Chứng minh tương tự cho hai góc $\hat{C A I}$ và $\hat{C D B}$ (hai góc cùng bù với góc $\hat{B A C}$ )

$\Rightarrow \hat{C A I} = \hat{C D B}$ .

b) Vì I, A, B thẳng hàng nên $\hat{A B D} = \hat{I B D}$ , do đó $\hat{I B D} = \hat{A C I}$

Vì I, C, D thẳng hàng nên $\hat{C D B} = \hat{I D B}$ , do đó $\hat{I D B} = \hat{C A I}$

Xét hai tam giác IDB và tam giác IAC có:

$\hat{I B D} = \hat{A C I}$ (chứng minh trên)

$\hat{I D B} = \hat{C A I}$ (chứng minh trên)

Do đó $Δ I D B$ đồng dạng với $Δ I A C$ (g – g)

c) Vì $Δ I D B$ đồng dạng với $Δ I A C$ $\Rightarrow \frac{I D}{I A} = \frac{I B}{I C}$ (hai cặp cạnh tương ứng tỉ lệ)

=> IA.IB = IC.ID

Dạng 2: Chứng minh đường thẳng vuông góc, ba điểm thẳng hàng

Phương pháp giải: Sử dụng các định lí, tính chất, hệ quả của góc ở tâm, góc nội tiếp.

Áp dụng quan hệ từ vuông góc đến song song, tiên đề Ơ clit.

Ví dụ 1: Cho đường tròn (O), đường kính AB và S là một điểm nằm bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M, N. Gọi P là giao điểm của BM và AN. Chứng minh SP vuông góc với AB.

Lời giải:

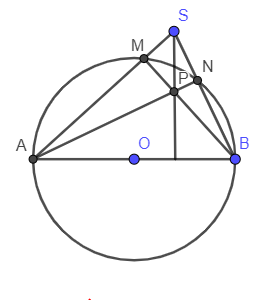
Bài tập về góc nội tiếp và cách giải – Toán lớp 9 (ảnh 1)

Vì $\hat{A M B}$ là góc nội tiếp chắn nửa đường tròn (do AB là đường kính)

$\Rightarrow \hat{A M B}$ là góc vuông

$\Rightarrow B M ⊥ S A$

$\Rightarrow B M$ là đường cao của tam giác SAB.

Vì $\hat{A N B}$ là góc nội tiếp chắn nửa đường tròn (do AB là đường kính)

$\Rightarrow \hat{A N B}$ là góc vuông

$\Rightarrow A N ⊥ S B$

$\Rightarrow A N$ là đường cao của tam giác SAB

Giao điểm của BM và AN là trực tâm tam giác SAB.

=> P là trực tâm của tam giác SAB.

$\Rightarrow S P ⊥ A B$ (điều phải chứng minh).

Ví dụ 2: Cho đường tròn (O) đường kính AB, điểm D thuộc đường tròn. Gọi E là điểm đối xứng với A qua D.

a) Tam giác ABE là tam giác gì?

b) Gọi K là giao điểm của EB với (O). Chứng minh OD vuông góc với AK.

Lời giải:

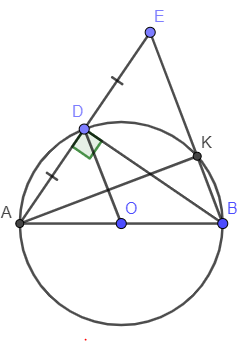
Bài tập về góc nội tiếp và cách giải – Toán lớp 9 (ảnh 1)

a) Ta có:

$\hat{A D B}$ là góc nội tiếp chắn nửa đường tròn (do AB là đường kính)

$\Rightarrow \hat{A D B}$ là góc vuông

$\Rightarrow \hat{A D B} = 90 °$

Xét tam giác ABE có:

$\hat{A D B} = 90 °$ nên $B D ⊥ A E$

=> BD là đường cao của tam giác ABE. (1)

Mặt khác A đối xứng với E qua D nên D là trung điểm cuả AE

=> BD là đường trung tuyến của tam giác ABE. (2)

Từ (1) và (2) ta thấy BD vừa là đường cao vừa là đường trung tuyến của tam giác ABE

=> Tam giác ABE là tam giác cân tại B.

b) Ta có:

D là trung điểm của AE

O là trung điểm của AB

Do đó DO là đường trung bình của tam giác ABE

=> DO // EB.

Lại có $\hat{A K B}$ là góc nội tiếp chắn nửa đường tròn (do AB là đường kính)

$\Rightarrow \hat{A K B}$ là góc vuông.

$\Rightarrow \hat{A K B} = 90 °$

$\Rightarrow A K ⊥ B E$

Ta có:

$\{\begin{cases} A K ⊥ B E \\ D O / / B E \end{cases} \Rightarrow A K ⊥ D O$ (quan hệ từ vuông góc đến song song).

III. Bài tập vận dụng

Bài 1: Cho nửa đường tròn (O) đường kính AB. Lấy M là điểm tùy ý trên nửa đường tròn (M khác A và B). Kẻ MH vuông góc với AB (H thuộc AB). Trên cùng nửa mặt phẳng bờ AB chứa nửa đường tròn (O) vẽ hai nửa đường tròn tâm $O_{1}$ , đường kính AH và đường tròn $O_{2}$ , đường kính BH. Đoạn MA và MB cắt hai nửa đường tròn $(O_{1})$ và $(O_{2})$ lần lượt tại P và Q. Chứng minh:

a) MH = PQ;

b) Các tam giác MPQ và MBA đồng dạng;

c) PQ là tiếp tuyến chung của hai đường tròn $(O_{1})$ và $(O_{2})$ .

Bài 2: Cho đường tròn (O) có các dây cung AB; BC; CA. Gọi M là điểm chính giữa cung nhỏ AB. Vẽ dây MN song song với BC. Gọi S là giao điểm của MN và AC. Chứng minh SM = SC và SN = SA.

Bài 3: Cho đường tròn (O) và hai dây song song AB, CD. Trên cung nhỏ AB lấy điểm M tùy ý. Chứng minh $\hat{A M C} = \hat{B M D}$ .

Bài 4: Cho đường tròn (O) và hai dây AM và BM vuông góc với nhau. Gọi I, K lần lượt là điểm chính giữa của các cung nhỏ MA và MB.

a) Chứng minh ba điểm A, O, B thẳng hàng.

b) Gọi P là giao điểm của AK và BI. Chứng minh P là tâm đường tròn nội tiếp tam giác MAB.

Bài 5: Cho đường tròn (O) và hai dây AB, AC bằng nhau. Qua A vẽ một cát tuyến cắt dây BC ở D và cắt (O) ở E. Chứng minh $A B^{2} = A H . A D$ .

Bài 6: Cho tam giác ABC nội tiếp đường tròn (O), hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AF.

a) Tứ giác BFCH là hình gì? Vì sao?

b) Gọi M là trung điểm của BC. Chứng minh rằng ba điểm H, M, F thẳng hàng.

c) Chứng minh AH = 2OM.

Bài 7: Cho tam giác ABC nội tiếp đường tròn (O; R), đường cao AH, biết AB = 8cm, AC = 15cm, AH = 5cm. Tính bán kính đường tròn (O).

Bài 8: Cho tam giác ABC có đường cao AH nội tiếp đường tròn (O), đường kính AD. Chứng minh: AB.AC = AH.AD.

Bài 9: Cho tam giác ABC (AB < AC) nội tiếp đường tròn (O). Vẽ đường kính MN vuông góc với BC (điểm M thuộc cung BC không chứa A). Chứng minh các tia AM, AN lần lượt là các tia phân giác của góc trong và các góc ngoài tại đỉnh A của tam giác ABC.

Bài 10: Cho nửa đường tròn (O) đường kính AB = 2R và điểm C nằm ngoài nửa đường tròn và cùng phía với nửa mặt phẳng có bờ là đường thẳng AB và chứa nửa đường tròn. Đường thẳng CA cắt nửa đường tròn ở M, CB cắt nửa đường tròn ở N. Gọi H là giao điểm của AN và BM.

a) Chứng minh CH vuông góc với AB.

b) Gọi I là trung điểm của CH. Chứng minh MI là tiếp tuyến của nửa đường tròn (O).

Bài 11: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Vẽ các đường kính AC và AD của hai đường tròn (O) và (O’). Chứng minh ba điểm B, C, D thẳng hàng.

Bài 12: Cho đường tròn (O) đường kính AB và một điểm C chạy trên một nửa đường tròn. Vẽ đường tròn (I) tiếp xúc với (O) tại C và tiếp xúc với đường kính AB tại D.

a) Nêu cách vẽ đường tròn (I) nói trên.

b) Đường tròn (I) cắt CA, CB lần lượt tại các điểm thứu hai là M, N. Chứng minh M, I, N thẳng hàng.

c) Chứng minh đường thẳng CD đi qua điểm chính giữa nửa đường tròn (O) không chứa C.