Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Cung chứa góc, các bài toán về quỹ tích, dựng hình (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 9.

Phương pháp giải Cung chứa góc, các bài toán về quỹ tích, dựng hình (50 bài tập minh họa)

I. Lý thuyết

1. Quỹ tích cung chứa góc

- Với đoạn thẳng AB và góc $\alpha \left(0°<\alpha <180°\right)$cho trước thì quỹ tích các điểm M thỏa mãn $\widehat{AMB}=\alpha$ là hai cung chứa góc $\alpha$ dựng trên đoạn AB.

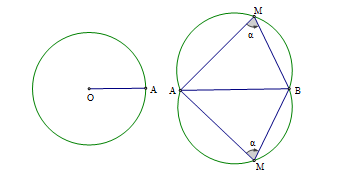
Chú ý:

- Hai cung chứa góc $\alpha$ nói trên ta gọi là hai cung tròn đối xứng nhau qua AB. Hai điểm A, B được coi là thuộc quỹ tích .

- Quỹ tích các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB.

2. Cách vẽ cung chứa góc $\mathit{\alpha }$

- Vẽ đường trung trung trực d của đoạn thẳng AB;

- Vẽ tia Ax tạo với AB một góc $\alpha$;

- Vẽ đường thẳng Ay vuông góc với Ax. Gọi O là giao điểm của Ay với d;

- Vẽ cung $\stackrel{⏜}{AmB}$, tâm O, bán kính OA sao cho cung này nằm ở nửa mặt phẳng bờ AB không chứa tia Ax. Cung $\stackrel{⏜}{AmB}$ được vẽ như trên là một cung chứa góc $\alpha$.

3. Cách giải một bài toán quỹ tích

Muốn chứng minh quỹ tích (tập hợp) các điểm M thỏa mãn tính chất T là một hình H nào đó ta là như sau:

Phần thuận: Mọi điểm có tính chất T đều thuộc hình H.

Phần nghịch: Mọi điểm thuộc hình H đều có tính chất T.

Từ đó đi đến kết luận quỹ tích các điểm M có tính chất T là hình H.

II. Các dạng toán

Dạng 1: Quỹ tích là cung chứa góc $\mathit{\alpha }$

Phương pháp giải:

Bước 1: Tìm tọa độ cố định trong hình vẽ.

Bước 2: Nối điểm phải tìm với hai đầu đoạn thẳng cố định đó, xác định góc $\alpha$không đổi.

Bước 3: Khẳng định quỹ tích điểm phải tìm là cung chứa góc $\alpha$ dựng trên đoạn cố định.

Ví dụ 1: Cho tam giác ABC, BC cố định, $\widehat{A}=50°$. Gọi D là giao điểm của ba đường phân giác trong của tam giác. Tìm quỹ tích điểm D.

Lời giải:

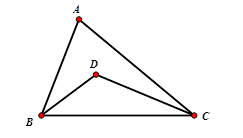
Xét tam giác ABC ta có:

$\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc trong một tam giác)

$\Rightarrow \widehat{B}+\widehat{C}=180°-50°$

$\iff \widehat{B}+\widehat{C}=130°$

Lại có:

 D là giao điểm của ba đường phân giác trong của tam giác ABC nên BD là phân giác $\widehat{B}$.

$\Rightarrow \widehat{DBC}=\frac{1}{2}\widehat{B}$

D là giao điểm của ba đường phân giác trong của tam gác ABC nên CD là phân giác $\widehat{C}$.

$\Rightarrow \widehat{DCB}=\frac{1}{2}\widehat{C}$

Do đó:

$\widehat{DBC}+\widehat{DCB}=\frac{1}{2}\widehat{B}+\frac{1}{2}\widehat{C}$

$\iff \widehat{DBC}+\widehat{DCB}=\frac{1}{2}\left(\widehat{B}+\widehat{C}\right)$

$\iff \widehat{DBC}+\widehat{DCB}=\frac{1}{2}.130°$

$\iff \widehat{DBC}+\widehat{DCB}=65°$

Xét tam giác BCD có:

$\widehat{BDC}+\widehat{DBC}+\widehat{DCB}=180°$

$\iff \widehat{BDC}+65°=180°$

$\iff \widehat{BDC}=180°-65°$

$\iff \widehat{BDC}=115°$

Do BC cố định nên quỹ tích điểm D là hai cung chứa góc $115°$dựng trên đoạn BC.

Ví dụ 2: Cho nửa đường tròn (O) đường kính AB. C là một điểm di động trên đường tròn. Ở phía ngoài tam giác ABC vẽ tam giác BCD vuông cân tại C. Tìm quỹ tích điểm D.

Lời giải:

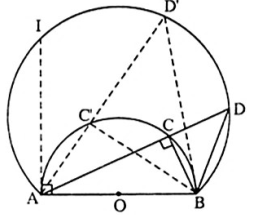
Phần thuận:

Ta có:

$\widehat{ACB}$ là góc nội tiếp chắn nửa đường tròn

$\Rightarrow \widehat{ACB}=90°$

Lại có:

$\widehat{DCB}$ (do tam giác BCD vuông cân tại C)

Do đó: $\widehat{ACB}+\widehat{DCB}=180°$

=> A, C, D thẳng hàng.

$\Rightarrow \widehat{ADB}=\widehat{CDB}=45°$ (do tam giác BCD vuông cân)

Vì AB cố định nên D nằm trên cung chứa góc $45°$dựng trên đoạn AB.

Dựng đường thẳng vuông góc với AB tại A, đường thẳng này giao với cung chứa góc $45°$dựng trên đoạn AB là I.

Nếu $C\equiv A\Rightarrow D\equiv I$

Phần đảo:

Lấy điểm D’ bất kỳ trên cung chứa góc $45°$ dựng trên đoạn Ab (D’ thuộc cung IB). Nối AD’ cắt nửa đường tròn (O) tại C’. Ta đi chứng minh tam giác BCD’ vuông cân tại C’

Ta có:

$\widehat{A{C}^{\text{'}}B}=90°$(góc nội tiếp chắn nửa đường tròn)

nên $\widehat{B{C}^{\text{'}}{D}^{\text{'}}}=90°$ (kề bù với góc $\widehat{A{C}^{\text{'}}B}$)

mà $\widehat{C^{\text{'}}{D}^{\text{'}}B}=45°$do đó tam giác BC’D’ vuông cân tại C’.

Vậy quỹ tích điểm D là cung BI của cung chứa góc $45°$dựng trên đoạn AB.

Dạng 2: Chứng minh nhiều điểm cùng thuộc một đường tròn và bài toán dựng hình

Phương pháp giải: Chứng minh nhiều điểm cùng thuộc nửa mặt phẳng bờ là AB và cùng nhìn đoạn cố định AB dưới một góc không đổi.

Ví dụ 1: Từ điểm S nằm ở ngoài đường tròn (O) kẻ tiếp tuyến SA; SB với A, B là tiếp điểm và cát tuyến SCD với đường tròn. Gọi I là trung điểm của CD. Chứng minh 5 điểm A, I, O, B, S cùng thuộc một đường tròn.

Lời giải:

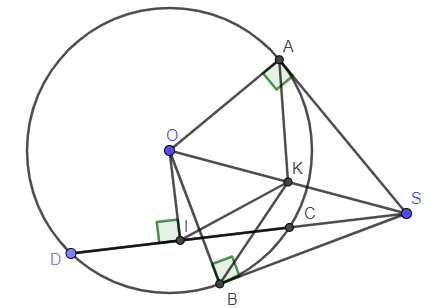
Vì SA là tiếp tuyến của đường tròn, A là tiếp điểm nên SA vuông góc với OA.

$\Rightarrow \widehat{SAO}=90°$

Vì SB là tiếp tuyến của đường tròn, B là tiếp điểm nên SB vuông góc với OB.

$\Rightarrow \widehat{SBO}=90°$

Vì I là trung điểm của CD nên OI vuông góc với CD (tính chất)

$\Rightarrow \widehat{SOI}=90°$

Gọi trung điểm của SO là K.

Tam giác OAS vuông tại A với K là trung điểm của SO

$\Rightarrow OK=KS=AK=\frac{1}{2}SO$ (định lí đường trung tuyến ứng với cạnh huyền)   (1)

Tam giác OBS vuông tại B với K là trung điểm của SO

$\Rightarrow OK=KS=BK=\frac{1}{2}SO$ (định lý đường trung tuyến ứng với cạnh huyền)   (2)

Tam giác OIS vuông tại I có K là trung điểm của SO

$\Rightarrow OK=KS=IK=\frac{1}{2}SO$ (định lí đường trung tuyến ứng với cạnh huyền)   (3)

Từ (1); (2); (3) $\Rightarrow OK=KS=IK=AK=BK=\frac{1}{2}SO$

Hay 5 điểm A, B, S, I, O cách đều điểm K.

Vậy 5 điểm A, B, S, I, O cùng nằm trên một đường tròn (K) bán kính KS.

Ví dụ 2: Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của hai đường chéo. Trên OA lấy điểm M sao cho OM = OB. Trên OB lấy N sao cho ON = OA. Chứng minh: 4 điểm D, M, N, C thuộc cùng một đường tròn.

Lời giải:

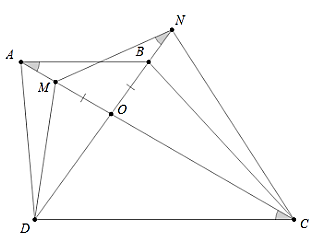
Xét tam giác OAB và tam giác OMN có:

$\widehat{AOB}$ chung

OA = ON

OB = OM

Do đó $\Delta AOB=\Delta NOM$ (c – g – c)

$\Rightarrow \widehat{BAO}=\widehat{MNO}$ (hai góc tương ứng)    (1)

Mặt khác, do ABCD là hình thang nên AB // CD (giả thuyết)

$\Rightarrow \widehat{BAO}=\widehat{DCO}$ (hai góc so le trong)    (2)

Từ (1) và (2) $\Rightarrow \widehat{MNO}=\widehat{DCO}$

Hai góc này cùng nhìn cạnh MD.

Do đó hai điểm N, C cùng nằm trên cung tròn dựng trên đoạn MD với góc $\widehat{DCO}$.

Ví dụ 3: Dựng hình thang cân ABCD (AB // CD), biết CD = 3cm, AC = 4cm, $\widehat{D}=70°$.

Lời giải:

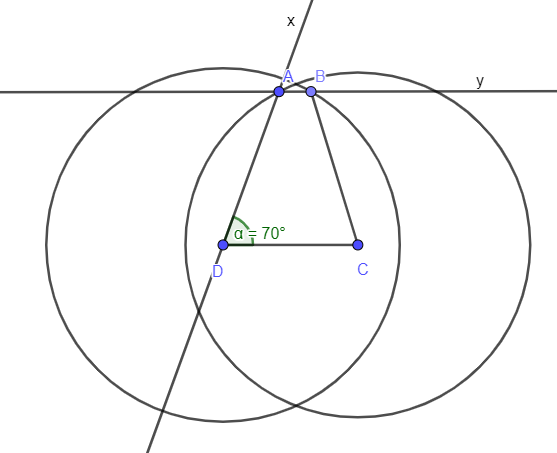
Cách dựng hình:

- Dựng đoạn CD = 3cm.

- Dựng góc $\widehat{CDx}=70°$.

- Trên nửa mặt phẳng bờ CD chứa tia Dx dựng đường tròn tâm C bán kính 4cm cắt Dx tại A.

- Dựng dây Ay song song với CD.

- Trên nửa mặt phẳng bờ CD chứa điểm A, dựng cung tròn tâm D bán kính 4cm cắt Ay tại B.

- Nối B với C ta được hình thang ABCD cần dựng.

III. Bài tập vận dụng

Bài 1: Cho tam giác ABC vuông tại A, BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm I khi A thay đổi.

Bài 2: Dựng tam giác vuông ABC với cạnh huyền BC = 4,5cm, AB = 2cm.

Bài 3: Cho nửa đường tròn đường kính AB. Gọi M là điểm chính giữa cung AB. Trên cung AM lấy điểm N. Trên tia đối của tia Am lấy điểm D sao cho MD = MB, trên tia đố tia NB lấy điểm E sao cho NA = NE, trên tia đối của tia MB lấy điểm C sao cho MC = MA. Chứng minh 5 điểm A, B, C, D, E cùng thuộc một đường tròn.

Bài 4: Dựng một cung chứa góc $55°$trên đoạn AB = 3cm

Bài 5: Cho I và O lần lượt là tâm đường tròn nội tiếp và ngoại tiếp tam giác ABC với $\widehat{A}=60°$. Gọi H là trực tâm của tam giác ABC. Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn.

Bài 6: Cho hình vuông ABCD. Trên cạnh BC lấy điểm E, trên tia đối của tia CD lấy điểm F sao cho CE = CF. Gọi M là giao điểm của hai đường thẳng DE và BF. Tìm quỹ tích điểm M khi E di động trên BC.

Bài 7: Cho cung AB cố định tạo bởi các bán kính OA, OB vuông góc với nhau, điểm I chuyển động trên cung AB. Trên tia OI lấy điểm M sao cho OM bằng tổng các khoảng cách từ điểm I đến OA, OB, Tìm quỹ tích các điểm M.

Bài 8: Cho tam giác ABC vuông tại A, phân giác BF. Từ điểm I nằm giữa B và F vẽ đường thẳng song song với AC cắt AB, BC lần lượt tại M và N. Vẽ đường tròn ngoại tiếp tam giác BIN cắt Ai tại D. Hai đường thẳng DN và BF cắt nhau tại E. Chứng minh:

a) Bốn điểm A, B, D, E cùng thuộc một đường tròn.

b) Năm điển A, B, C, D, E cùng thuộc một đường tròn. Từ đó suy ra BE vuông góc với CE.

Bài 9: Từ điểm M nằm bên ngoài đường tròn (O), kẻ cát tuyến MAB đi qua O và các tiếp tuyến MC, MD. Gọi K là giao điểm của AC và BD. Chứng minh 4 điểm B, C, M, K thuộc cùng một đường tròn.

Bài 10: Cho đường tròn đường kính AB cố định, M là một điểm chạy trên đường tròn. Trên tia đối của tia MA lấy điểm I sao cho MI = 2MB.

a) Chứng minh $\widehat{AIB}$ không đổi.

b) Tìm tập hợp tất cả các điểm I nói trên.