Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Độ dài đường tròn, độ dài cung tròn (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 9.

Phương pháp giải Độ dài đường tròn, độ dài cung tròn (50 bài tập minh họa)

I. Lý thuyết

1. Công thức tính độ dài đường tròn (chu vi đường tròn)

Độ dài (C) của một đườn tròn bán kính R được tính theo công thức:

$C=2\pi R$ hoặc $C=\pi d$ (với d = 2R)

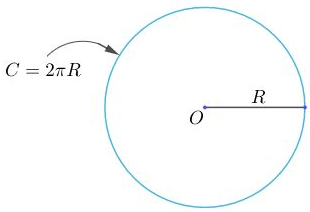
2. Công thức tính độ dài cung tròn

Trên đường tròn bán kính R, độ dài l của một cung $n°$được tính theo công thức

$l=\frac{\pi Rn}{180}$

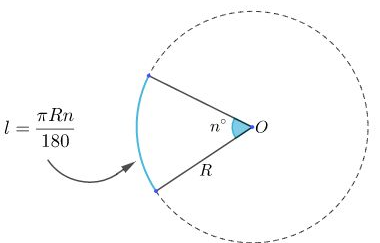
II. Các dạng bài tập

Dạng 1: Tính độ dài đường tròn, cung tròn và các đại lượng liên quan

Phương pháp giải: Áp dụng công thức đã nếu trong phần lí thuyết.

Ví dụ 1: Lấy giá trị gần đúng của $\pi =3,14$, hãy điền vào ô trống trong bảng sau (đơn vị đo độ dài là cm, làm tròn kết quả đến chữ số thập phân thứ hai).

Lời giải:

Với R = 9cm thì đường kính của đường tròn là d = 2.9 = 18cm và chu vi của đường tròn là C = 18.3,14 = 56,52cm.

Với d = 16cm thì bán kính đường tròn là R = 16:2 = 8cm và chu vi của đường tròn là C = 16.3,14 = 50,24cm.

Với R = 3cm thì đường kính đường tròn là d = 3.2 = 6cm và chu vi của đường tròn là C = 6.3,14 = 18,84cm.

Với d = 6cm thì bán kính đường tròn là R = 3cm và chu vi đường tròn là C = 6.3,14 = 18,84cm.

Với C = 30cm thì đường kính của đường tròn là d = 30:3,14 = 9,55cm và bán kính đường tròn là R = 9,55:2 = 4,78cm.

Với C = 25,12cm thì đường kính của đường tròn d = 25,12:3,14 = 8cm và bán kính đường tròn R = 8:2 = 4cm.

Ta có bảng sau:

Ví dụ 2: Tính độ dài cung $50°$của một đường tròn có bán kính là 3cm.

Lời giải:

Áp dụng công thúc độ dài cung tròn $l=\frac{\pi Rn}{180}$ta có:

Độ dài cung $50°$của đường tròn bán kính 3cm là:

$l=\frac{\pi \mathrm{.3.50}}{180}=\frac{5\pi }{6}$ (cm).

Ví dụ 3: Tính chu vi một vành một cái nón lá có bán kính là 25cm.

Lời giải:

Áp dụng công thức tính chu vi đường tròn ta được:

Chu vi vành một cái nón là C = 2R.$\pi$= 2.25.$\pi$= 50(cm).

Dạng 2: Tính độ dài cung tròn do các cung chắp nối thành

Phương pháp giải: Chia độ dài cung tròn mình cần tính thành các cung tròn nhỏ hơn của đường tròn khác sau đó sử dụng công thức tính độ dài cung tròn.

Ví dụ 1: Cho hình vẽ:

Biết OA = 4cm. Tính chu vi của hình

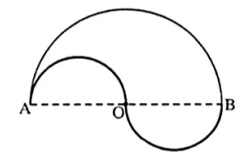
Lời giải:

Độ dài cung OA là

$l_1=\frac{\pi \mathrm{.4.180}}{180}=4\pi \left(cm\right)$

Do AB là đường kính của (O) nên OA = OB = 4cm; AB = 8cm.

Độ dài cung OB là

$l_2=\frac{\pi \mathrm{.4.180}}{180}=4\pi \left(cm\right)$

Độ dài cung AB là:

$l_3=\frac{\pi \mathrm{.8.180}}{180}=8\pi \left(cm\right)$

Chu vi hình cần tính là

C = $l_1+l_2+l_3=4\pi +4\pi +8\pi =16\pi \left(cm\right)$

Ví dụ 2: Cho hình vẽ:

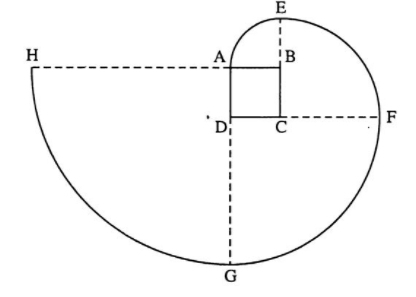
Biết AB = 1cm Tính độ dài đường cong AEFGH.

Lời giải:

Đường cong AE là cung của đường tròn bán kính AB = 1cm.

Độ dài đường cong AE là:

$l_1=\frac{\mathrm{1.90.}\pi }{180}=\frac{\pi }{2}\left(cm\right)$

Đường cong EF là cung của đường tròn bán kính CE = CB + BE = 1 + 1 = 2cm.

Độ dài đường cong EF là:

$l_2=\frac{\mathrm{2.90.}\pi }{180}=\pi \left(cm\right)$

Đường cong FG là cung của đường tròn bán kính DF = DC + CF = 1 + 2 = 3cm.

Độ dài đường cong FG là:

$l_3=\frac{\mathrm{3.90.}\pi }{180}=\frac{3\pi }{2}\left(cm\right)$

Đường cong GH là cung của đường tròn bán kính AG = AD + DG = 1 + 3 = 4cm

Độ dài đường cong HG là

$l_4=\frac{\mathrm{4.90.}\pi }{180}=2\pi \left(cm\right)$

Độ dài đường cong AEFGH là:

$l_1+l_2+l_3+l_4=\frac{\pi }{2}+\pi +\frac{3\pi }{2}+2\pi =5\pi$(cm)

Dạng 3: So sánh độ dài các cung

Phương pháp giải:

- Tính độ dài cung theo bán kính R và số đo của cung

- Sau khi thu được kết quả ta tiến hành so sánh.

Ví dụ 1: AB là đường kính của nửa đường tròn. Trên đoạn thẳng AB lấy hai điểm M và N sao cho M nằm giữa A và N. Vẽ các đường tròn có đường kính AM, MN, NB. Hãy chứng minh tổng độ dài các cung AM, MN, NB bằng độ dài cung AB.

Lời giải:

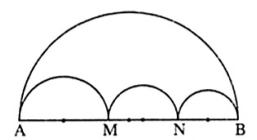
Gọi $C_1;C_2;C_3;C$là độ dài nửa đường tròn đường kính AM; MN; NB; AB.

$C_1=\frac{1}{2}\pi .AM$ (đơn vị độ dài)

$C_2=\frac{1}{2}.\pi .MN$ (đơn vị độ dài)

$C_3=\frac{1}{2}.\pi .NB$(đơn vị độ dài)

$C=\frac{1}{2}.\pi .AB$ (đơn vị độ dài)

Lấy $C_1+C_2+C_3=\frac{1}{2}\pi .AM+\frac{1}{2}.\pi MN+\frac{1}{2}.\pi .NB$

$\iff C_1+C_2+C_3=\frac{1}{2}\pi .\left(AM+MN+NB\right)$

$\iff C_1+C_2+C_3=\frac{1}{2}\pi .AB=C$(điều phải chứng minh)

Ví dụ 2: So sánh độ dài cung $\stackrel{⏜}{OmB}$ và $\stackrel{⏜}{AB}$.

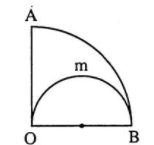
Lời giải:

Gọi $l_1$là độ dài cung $\stackrel{⏜}{OmB}$

Gọi $l_2$là độ dài cung $\stackrel{⏜}{AB}$

Độ dài cung $\stackrel{⏜}{OmB}$là

$l_1=\frac{1}{2}.\pi .OB$ (đơn vị độ dài)

Độ dài cung $\stackrel{⏜}{AB}$ là

$l_2=\frac{1}{4}.\pi \mathrm{.2.}OB =\frac{1}{2}.\pi .OB$(đơn vị độ dài)

Vậy $l_1=l_2$

III. Bài tập tự luyện

Bài 1: Cho $\pi =3,14$. Hãy điền vào ô trống

Bài 2: Hãy điền vào ô trống:

Bài 3: Cho tam giác ABC có AB = AC = 3cm và $\widehat{A}=120°$. Tính độ dài đường tròn ngoại tiếp tam giác ABC.

Bài 4: Cho đường tròn (O), bán kính R và dây AB. Cho hai trường hợp sau:

a) Nếu số đo cung AB bằng $90°$. Hãy tính chu vi đường tròn đường kính AB.

b) Nếu độ dài cung AB bằng $\frac{5\pi R}{6}$. Hỏi số đo  của góc $\widehat{AOB}$ bằng bao nhiêu.

Bài 5: Cho đường tròn (O) bán kính OA. Từ trung điểm M của OA vẽ dây BC vuông góc với OA. Biết độ dài đường tròn (O) là $4\pi$ cm. Tính:

a) Bán kính đường tròn (O);

b) Độ dài cung BC của đường tròn.

Bài 6: Cho tam giác AB vuông tại A có AB = 5cm, $\widehat{B}=60°$. Đường tròn tâm I đường kính AB cắt BC ở D.

a) Chứng minh AD vuông góc với BC.

b) Chứng minh đường tròn tâm K đường kính AC đi qua D.

c) Tính độ dài cung nhỏ BD.

Bài 7: Tứ giác ABCD ngoại tiếp đường tròn (O), vẽ các nửa đường tròn đường kính AD và BC ra phía ngoài của tứ giác. Biết AB + CD = 10cm. Tính tổng các độ dài của hai nửa đường tròn này.

Bài 8: Tính chu vi các phần bị gạch trong các hình vẽ dưới đây:

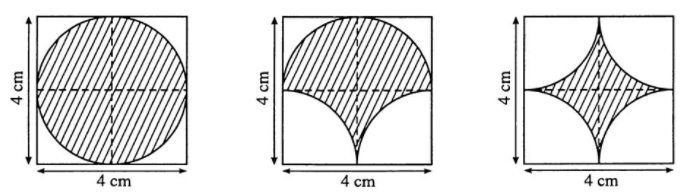
Bài 9: Cho tứ giác ABCD ngoại tiếp đường tròn (O). Vẽ ra phía ngoài tứ giác này bốn nửa đường tròn đường kính lần lượt là bốn cạnh của tứ giác. Chứng minh rằng tổng độ dài của hai nửa đường tròn có đường kính là hai cạnh đối diện của tứ giác bằng tổng độ dài hai nửa đường tròn có đường kính là hai cạnh đối diện còn lại.

Bài 10: Cho nửa đường tròn (O; R) đường kính AB. Vẽ dây CD = R (thuộc cung AD). Nối AC với BD cắt nhau tại M.

a) Chứng minh tam giác MCD đồng dạng với tam giác MBA, tìm tỉ số đồng dạng.

b) Cho $\widehat{ABC}=30°$. Tính độ dài cung nhỏ AC.