Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Tọa độ của vectơ, tọa độ của một điểm (HAY NHẤT 2024) gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:
Nội dung bài viết
Phương pháp giải Tọa độ của vectơ, tọa độ của một điểm (HAY NHẤT 2024)
A. Lí thuyết
- Tọa độ của điểm trên trục: Cho M là một điểm tùy ý trên trục (O;→e). Khi đó tồn tại duy nhất một số k sao cho →OM=k→e. Ta gọi số k đó là tọa độ của điểm M trên trục (O;→e).
- Tọa độ của vectơ trên trục: Cho hai điểm A và B trên trục (O;→e). Khi đó tồn tại duy nhất một số k sao cho →AB=k→e. Độ dài đại số của →AB đối với trục (O;→e) kí hiệu là ¯AB. Nếu →AB cùng hướng với →e thì ¯AB>0. Nếu →AB ngược hướng với →e thì ¯AB<0. Nếu hai điểm A và B trên trục (O; →e) có tọa độ lần lượt là a và b thì ¯AB= b – a.
- Tọa độ trung điểm I đoạn thẳng AB trên trục (O;→i) là: xI=xA+xB2.
- Tọa độ của vectơ trong mặt phẳng Oxy: Có →u=(x;y)⇔→u=x→i+y→j. Cho hai điểm A(xA;yA) và B(xB;yB) ta có: →AB=(xB−xA;yB−yA).
- Tọa độ của điểm trong mặt phẳng Oxy: Có M(x;y)⇔→OM=x→i+y→j.
- Tọa độ trung điểm I (xI;yI) của đoạn thẳng AB là: xI=xA+xB2;yI=yA+yB2.
- Tọa độ của trọng tâm G (xG;yG) của tam giác ABC được tính theo công thức:
xG=xA+xB+xC3;yG=yA+yB+yC3→v=(v1;v2)
- Điều kiện để hai vectơ cùng phương: Hai vectơ →u=(u1;u2) và →v=(v1;v2) với →v≠→0 cùng phương khi và chỉ khi có số k sao cho u1=kv1 và u2=kv2. Nếu k > 0 thì →u cùng hướng với →v, ngược lại, nếu k < 0 thì →u ngược hướng với →v.
- Hai vectơ bằng nhau khi chúng có hoành độ bằng nhau và tung độ bằng nhau.
- Cho →u=(u1;u2) và , khi đó:
→u+→v=(u1+v1;u2+v2)k.→u=(ku1;ku2),k∈ℝ
B. Các dạng bài
Dạng 1: Tìm tọa độ của một điểm, tọa độ của vectơ trên trục và trong mặt phẳng Oxy.
Phương pháp giải:
Áp dụng lí thuyết về tọa độ của điểm, tọa độ của vectơ trên trục và tọa độ của điểm, tọa độ của vectơ trong mặt phẳng Oxy, tọa độ của trung điểm đoạn thẳng, tọa độ của trọng tâm tam giác, các tính chất của vectơ để xác định tọa độ của điểm và tọa độ của vectơ theo yêu cầu đề bài.
Ví dụ minh họa:
Bài 1: Trên trục tọa độ cho 2 điểm A, B có tọa độ lần lượt là -2; 1. Tìm tọa độ của vectơ và tọa độ trung điểm I của đoạn thẳng AB.
Giải:
Ta có:
Tọa độ của vectơ trên trục tọa độ là 3.
Tọa độ điểm I là: .
Bài 2: Trong mặt phẳng Oxy, cho 3 điểm A (-3;1), B (2;4) và C (2;1). Tìm tọa độ trọng tâm G của tam giác ABC, tọa độ trung điểm đoạn thẳng AB, AC.
Giải:
Áp dụng công thức tọa độ trọng tâm tam giác ta có:
Áp dụng công thức tọa độ trung điểm đoạn thẳng ta có:
Gọi I là trung điểm của đoạn thẳng AB có:
Gọi J là trung điểm của đoạn thẳng AC có:
Dạng 2: Xác định tọa độ điểm, vectơ liên quan đến biểu thức dạng , và .
Phương pháp giải:
Áp dụng công thức tính tọa độ của các vectơ , và .
Ví dụ minh họa:
Bài 1: Cho hai vectơ và . Tính tọa độ các vectơ , và với k = 5.
Giải:
+) Ta có:
= ( 3 + 1 ; -2 + 6 ) = (4;4).
+) Ta có:
+) Ta có:
Bài 2: Trong mặt phẳng Oxy, cho các điểm A (1;3) và B (4;0). Tìm tọa độ điểm M thỏa mãn .
Giải:
Gọi tọa độ điểm M là ( x;y)
+) Tọa độ vectơ là: = ( 4 – 1 ; 0 – 3 ) = ( 3;-3 )
+) Tọa độ vectơ là: = ( x – 1 ; y – 3 )
+) Ta có:
M = ( 0;4 )
Dạng 3: Bài toán liên quan đến sự cùng phương của hai vectơ. Phân tích một vectơ qua hai vectơ không cùng phương.
Phương pháp giải:
Áp dụng điều kiện để hai vectơ cùng phương liên quan đến tọa độ: Hai vectơ và với cùng phương khi và chỉ khi có một số k sao cho và . Nếu k > 0 thì cùng hướng với , ngược lại, nếu k < 0 thì ngược hướng với . Để phân tích qua hai vectơ và không cùng phương, ta giả sử . Khi đó ta quy về giải hệ phương trình
Ví dụ minh họa:
Bài 1: Cho A (1;2), B (-2;6). Điểm M nằm trên trục Oy sao cho ba điểm A, B, M thẳng hàng. Tìm tọa độ điểm M .
Giải:
Ta có: M nằm trên trục Oy M = (0;y)
Ta có: , .
Ba điểm A, B, M thẳng hàng cùng phương với
Bài 2: Cho các vectơ , và . Phân tích vectơ theo hai vectơ và .
Giải:
Giả sử
C. Bài tập vận dụng
Bài 1: Trên trục tọa độ (O;) cho 2 điểm A, B có tọa độ lần lượt là 3 và -5. Tìm tọa độ trung điểm I của đoạn thẳng AB.
Đáp án: .
Bài 2: Trong mặt phẳng Oxy, cho điểm M (x;y). Tìm tọa độ của điểm M’ đối xứng với M qua trục hoành.
Đáp án: M’ (x;-y)
Bài 3: Trong mặt phẳng Oxy, cho hình vuông ABCD tâm I và có A (1;3). Biết điểm B thuộc trục Ox và cùng hướng với . Tìm tọa độ vectơ .
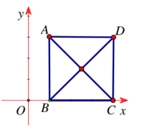
Đáp án: = (3;-3)
Bài 4: Trong mặt phẳng Oxy, cho hình thoi ABCD cạnh a. Biết , A trùng với gốc tọa độ O; C thuộc Ox và . Tìm tọa độ đỉnh B, C của hình thoi ABCD.
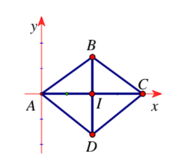
Đáp án:
Bài 5: Cho , và . Vectơ . Tìm x.
Đáp án: x = 15.
Bài 6: Trong mặt phẳng Oxy, cho các điểm A (-3;3) , B (1;4) , C (2;-5). Tìm tọa độ điểm M thỏa mãn: .
Đáp án:
Bài 7: Cho , , . Tính tọa độ vectơ .
Đáp án:
Bài 8: Cho 4 điểm A (1;-2) , B (0;3) , C (-3;4) , D (-1;8). Ba điểm nào trong 4 điểm đã cho là thẳng hàng ?
Đáp án: Ba điểm A, B, D.
Bài 9: Trong mặt phẳng Oxy, cho ba điểm A (6;3) , B (-3;6) . Xác định điểm D trên trục tung sao cho A, B, D thẳng hàng.
Đáp án: D = (0;5)
Bài 10: Trong mặt phẳng Oxy, cho A (m-1;-1) , B (2;2-2m) , C (m+3;3). Tìm m để A, B, C là ba điểm thẳng hàng.
Đáp án: m = 0.
D. Bài tập tự luyện
Câu 1. Trong mặt phẳng Oxy, cho hai điểm A(1; 2) và B(–2; 3). Gọi B’ là điểm đối xứng của B qua A. Tọa độ điểm B’ là:
A. B’(4; 1);
B. B’(0; 1);
C. B’(–4; –1);
D. B’(0; –1).
Câu 2. Cho mặt phẳng Oxy, cho ∆ABC có G là trọng tâm. Biết B(4; 1), C(1; –2) và G(2; 1). Tọa độ điểm A là:
A. A(1; 4);
B. A(3; 0);
C. A(4; 1);
D. A(0; 3).
Câu 3. Trong mặt phẳng Oxy, cho ba điểm A(–2; –3), B(1; 4) và C(3; 1). Đặt . Tọa độ của là:
A. (–2; 3);
B. (–8; –11);
C. (2; –3);
D. (8; 11).
Câu 4. Trong mặt phẳng Oxy, cho ba điểm A(1; 5), B(–1; 0) và C(1; 3). M là điểm nằm trên trục Oy sao cho cùng phương với . Tọa độ điểm M là:
A.
B.
C.
D.
Câu 5. Trong mặt phẳng Oxy, cho và . Tính .
A. 6;
B. 2;
C. 4;
D. –4
Câu 6. Cho và . Tìm a để .
A. ;
B. ;
C. ;
D. .
Câu 7. Trong mặt phẳng Oxy, cho và . Kết luận nào sau đây sai?
A. ;
B. ;
C. ;
D. .
Câu 8. Trong mặt phẳng Oxy, cho , . Tìm x để và cùng phương
A. x = –5;
B. x = 4;
C. x = 0;
D. x = –1.
Câu 9. Trong mặt phẳng Oxy, cho , . Tìm tọa độ của sao cho .
A. ;
B. ;
C. ;
D. .
Câu 10. Trong mặt phẳng Oxy, cho ba điểm A(–1; 1), B(1; 3), C(5; 2). Tọa độ điểm D là đỉnh thứ tư của hình bình hành ABCD là:
A. (3; –2);
B. (5; 0);
C. (3; 0);
D. (5; –2).
Câu 11. Trong mặt phẳng Oxy, cho hai điểm A(1; 2) và B(–1; 5). Tìm m để điểm C(2; m) thuộc đường thẳng AB.
A. m = 1;
B. ;
C. ;
D. m = 2.
Câu 12. Cho hai điểm A(6; –1) và B(x; 9). Giá trị của x để khoảng cách giữa A và B bằng là:
A. x ∈∅;
B. x = 1;
C. x = 11;
D. x = 11 hoặc x = 1.
Câu 13. Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có A(0; 3), D(2; 1) và I(–1; 0) là tâm của hình chữ nhật. Tọa độ trung điểm của đoạn thẳng BC là:
A. (–3; –2);
B. (–2; 1);
C. (4; –1);
D. (1; 2).
Câu 14. Cho , . Góc giữa hai vectơ và bằng
A. 45°;
B. 60°;
C. 90°;
D. 135°.
Câu 15. Trong mặt phẳng Oxy, cho ∆ABC có A(–3; 0), B(3; 0) và C(2; 6). Gọi H(a; b) là trực tâm của ∆ABC. Giá trị của a + 6b bằng:
A. 3;
B. 6;
C. 7;
D. 5.
Xem các Phương pháp giải bài tập hay, chi tiết khác:
Trọn bộ công thức cơ bản về Vectơ dầy đủ
Công thức về tổng và hiệu hai vectơ chi tiết nhất
Quy tắc trung điểm, trọng tâm, quy tắc hình bình hành vecto lớp 10 chi tiết nhất
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.