Toptailieu.vn biên soạn và giới thiệu giải Giải Vở thực hành Toán 8 (Kết nối tri thức) Bài Luyện tập chung trang 13 hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập Toán 8. Mời các bạn cùng đón xem:
Nội dung bài viết
Giải Vở thực hành Toán 8 (Kết nối tri thức) Bài Luyện tập chung tràn 13
Bài 1 trang 13 VTH Toán 8 Tập 1: Cho các biểu thức:
45x; (√2−1)xy; −3xy2; 12x2y; 1xy3; −xy+√2; −32x2y; √x5.
a) Trong các biểu thức đã cho, biểu thức nào là đơn thức? Biểu thức nào không là đơn thức?
b) Hãy chỉ ra hệ số và phần biến của mỗi đơn thức đã cho.
c) Viết tổng tất cả các đơn thức trên để được một đa thức. Xác định bậc của đa thức đó.
Lời giải:
a) Biểu thức 1xy3 không là đơn thức.
Biểu thức −xy+√2 không là đơn thức.
Biểu thức √x5 không là đơn thức.
Các biểu thức còn lại đều là đơn thức.
b) - Đơn thức 45x có hệ số là 45 và phần biến là x.
- Đơn thức (√2−1)xy có hệ số là √2−1 và phần biến là xy.
- Đơn thức −3xy2 có hệ số là −3 và phần biến là xy2.
- Đơn thức 12x2y có hệ số là 12 và phần biến là x2y.
- Đơn thức −32x2y có hệ số là −32 và phần biến là x2y.
c) Tổng tất cả các đơn thức trên là:
45x+(√2−1)xy+(−3xy2)+12x2y+(−32x2y)
= 45x+(√2−1)xy−3xy2−x2y.
Đa thức 45x+(√2−1)xy−3xy2−x2y có bậc là 3.
a) Hãy tìm đơn thức (hai biến x và y) biểu thị số mét khối nước cần có để bơm đầy cả hai bể bơi.
b) Tính lượng nước bơm đầy bể nếu x = 5 m, y = 3 m.
Lời giải:
a) Bể thứ nhất có chiều sâu 1,2 m với hai kích thước đáy là x và y nên có dung tích V1 = 1,2xy (m3). Bể thứ hai có chiều sâu 1,5 m với các kích thước đáy là 5x và 5y nên có dung tích là V2 = 1,5.5x.5y = 37,5xy (m3).
Do đó số mét khối nước cần có để bơm đầy cả hai bể bơi là
V = V1 + V2 = 1,2xy + 37,5xy = (1,2 + 37,5)xy = 38,7xy (m3).
b) Khi x = 5 m, y = 3 m, lượng nước bơm đầy hai bể là
V = 38,7.5.3 = 580,5 (m3).
a) P = 5x4 – 3x3y + 2xy3 – x3y + 2y4 – 7x2y2 – 2xy3.
b) Q = x3 + x2y – xy2 – x2y – xy2 – x3.
Lời giải:
a) P = 5x4 – 3x3y + 2xy3 – x3y + 2y4 – 7x2y2 – 2xy3
= 5x4 – (3x3y + x3y) + (2xy3 – 2xy3) + 2y4 – 7x2y2
= 5x4 – 4x3y + 2y4 – 7x2y2.
Tất cả các hạng tử đều có bậc 4.
Vậy P là đa thức bậc 4.
Tại x = 1; y = −2, ta có
P=5.14−4.13.(−2)+2.(−2)4−7.12.(−2)2=17.
b) Q = x3 + x2y – xy2 – x2y – xy2 – x3
= (x3 – x3) + (x2y – x2y) – (xy2 + xy2) = –2xy2.
Đa thức Q có bậc là 3.
Tại x = 1; y = −2, ta có:
Q = –2xy2 = –2.1.(−2)2 = –2.4 = –8.
Bài 4 trang 14 VTH Toán 8 Tập 1: Cho hai đa thức:
A = 7xyz2 – 5xy2z + 3x2yz – xyz + 1; B = 7x2yz – 5xy2z + 3xyz2 – 2.
a) Tìm đa thức C sao cho A – C = B.
b) Tìm đa thức D sao cho A + D = B.
c) Tìm đa thức E sao cho E – A = B.
Lời giải:
a) C = A – B = (7xyz2 – 5xy2z + 3x2yz – xyz + 1) – (7x2yz – 5xy2z + 3xyz2 – 2)
= 7xyz2 – 5xy2z + 3x2yz – xyz + 1 – 7x2yz + 5xy2z – 3xyz2 + 2
= (7xyz2 – 3xyz2) + (5xy2z – 5xy2z) + (3x2yz – 7x2yz) – xyz + (1 + 2)
= 4xyz2 – 4x2yz – xyz + 3.
b) D = B – A = –(A – B) = –(4xyz2 – 4x2yz – xyz + 3)
= –4xyz2 + 4x2yz + xyz – 3.
c) E = A + B = (7xyz2 – 5xy2z + 3x2yz – xyz + 1) + (7x2yz – 5xy2z + 3xyz2 – 2)
= 7xyz2 – 5xy2z + 3x2yz – xyz + 1 + 7x2yz – 5xy2z + 3xyz2 – 2
= (7xyz2 + 3xyz2) – (5xy2z + 5xy2z) + (7x2yz + 3x2yz) – xyz + (1 – 2)
= 10x2yz – 10xy2z + 10xyz2 – xyz + 3.
Lời giải:
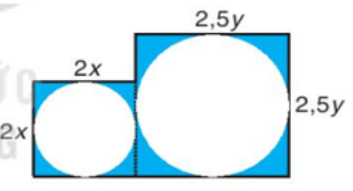
Miếng bìa gồm có hai hình vuông có cạnh lần lượt là 2x và 2,5y ghép lại. Do đó diện tích của miếng bìa là 2x.2x + 2,5y.2,5y = 4x2 + 6,25y2.
Tổng diện tích hai hình tròn cắt ra là (2x)2.π + (2,5y)2.π = 4πx2 + 6,25πy2.
Vậy diện tích phần còn lại của miếng bìa là
(4x2 + 6,25y2) − (4πx2 + 6,25πy2) = 4(1 − π)x2 + 6,25(1 − π)y2.
Đó là một đa thức bậc 2.
Tính M + N – P và M – N – P.
Lời giải:
+) N + N − P = (3x3 – 4x2y + 3x – y) + (5xy – 3x + 2) – (3x3 + 2x2y + 7x – 1)
= 3x3 – 4x2y + 3x – y + 5xy – 3x + 2 – 3x3 – 2x2y – 7x + 1
= (3x3 – 3x3) – (4x2y + 2x2y) + 5xy + (3x – 3x – 7x) – y + (2 + 1)
= – 6x2y + 5xy – 7x – y + 3.
+) M – N – P = (3x3 – 4x2y + 3x – y) – (5xy – 3x + 2) – (3x3 + 2x2y + 7x – 1)
= 3x3 – 4x2y + 3x – y + 5xy + 3x – 2 – 3x3 – 2x2y – 7x + 1
= (3x3 – 3x3) – (4x2y + 2x2y) + 5xy + (3x + 3x – 7x) – y + (1 – 2)
= – 6x2y + 5xy – x – y – 1.
Lời giải:
Ta có:
A + B = (x2y2 − axy2 + 3y2 − xy + b) + (cx2y2 + 2xy2 − dy2 + 4)
= (1 + c)x2y2 + (2 − a)xy2 + (3 − d)y2 − xy + (b + 4).
Theo đề bài, (1 + c)x2y2 + (2 − a)xy2 + (3 − d)y2 − xy + (b + 4) = −2x2y2 + 3y2 − xy − 1.
So sánh hệ số của các hạng tử đồng dạng ở hai vế, ta có:
1 + c = −2 (hệ số của x2y2), suy ra c = −3; 3 − d = 3 (hệ số của y2), suy ra d = 0; 2 − a = 0 (hệ số của xy2), suy ra a = 2; b + 4 = −1 (hệ số tự do), suy ra b = −5.
Vậy đáp số của bài toán là a = 2, b = −5, c = −3 và d = 0.
Xem thêm Lời giải bài tập Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác:
Bài 3: Phép cộng và phép trừ đa thức
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.