Với Giải Bài 18 trang 74 sách bài tập Toán 8 Tập 1 trong Bài tập cuối chương 3 Sách bài tập Toán lớp 8 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán lớp 8.
Cho hình chữ nhật ABCD có AB = 2BC. Gọi I là trung điểm của AB và K là trung điểm của CD
Bài 18 trang 74 sách bài tập Toán 8 Tập 1: Cho hình chữ nhật ABCD có AB = 2BC. Gọi I là trung điểm của AB và K là trung điểm của CD. Chứng minh:
a) AIKD và BIKC là hình vuông.
b) và .
Lời giải:
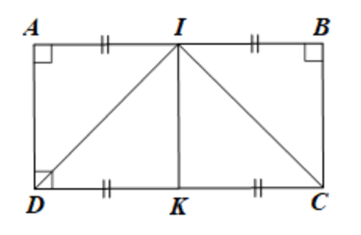
a) VìI là trung điểm của AB nên (1)
Vì K là trung điểm của CD nên (2)
Vì ABCD là hình chữ nhật nên AB = CD. (3)
Từ (1), (2) và (3) suy ra .
Ta có AB = 2BC,
suy ra , suy ra .
Xét tứ giác AIKD có: AI // DK (vì ABCD là hình chữ nhật); AI = DK (chứng minh trên)
Suy ra tứ giác AIKD là hình bình hành.
Ta lại có AI = AD nên AIKD là hình thoi.
Mà nên AIKD là hình vuông.
Tương tự, tứ giác BIKC có: BI // CKvà BI = CKnên BIKC là hình bình hành.
Lại có BI = BC nên BIKC là hình thoi.
Mà nên BIKC là hình vuông.
b) Vì AIKD là hình vuông nên .
Suy ra .
Vì AIKD là hình vuông nên ID là đường phân giác của .
Suy ra .
Vì BIKC là hình vuông nên IC là đường phân giác của .
Suy ra .
Do đó .
Vậy .
Xem thêm các bài giải sách bài tậpToán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Câu 1 trang 72 sách bài tập Toán 8 Tập 1: Cho tam giác MNP vuông tại M. Biết MN = 40, MP = 9. Độ dài cạnh NP bằng
Câu 2 trang 72 sách bài tập Toán 8 Tập 1: Ba số nào sau đây không thể là độ dài ba cạnh của một tam giác vuông?
Câu 3 trang 72 sách bài tập Toán 8 Tập 1: Một tứ giác có số đo ba góc lần lượt bằng 80°, 40°, 100°. Số đo góc còn lại bằng
Câu 4 trang 72 sách bài tập Toán 8 Tập 1: Cho hình thang cân có độ dài hai đáy lần lượt là 10 cm và 4 cm, độ dài cạnh bên là 5 cm. Hình thang đó có chiều cao là
Câu 5 trang 72 sách bài tập Toán 8 Tập 1: Cho hình bình hành MNPQ có O là giao điểm của hai đường chéo. Biết MN = 6, OM = 3, ON = 4. Độ dài của MP, NQ, PQ lần lượt là
Câu 6 trang 73 sách bài tập Toán 8 Tập 1: Cho hình thoi EFGH có hai đường chéo cắt nhau tại O. Biết OE = 6, OF = 8. Độ dài cạnh EF là
Câu 7 trang 73 sách bài tập Toán 8 Tập 1: Một hình vuông có diện tích bằng diện tích của hình chữ nhật có hai cạnh bằng 2 cm và 18 cm. Độ dài cạnh của hình vuông bằng
Câu 8 trang 73 sách bài tập Toán 8 Tập 1: Một hình vuông có cạnh bằng cm. Độ dài đường chéo của hình vuông bằng
Câu 9 trang 73 sách bài tập Toán 8 Tập 1: Một hình bình hành có thể không có tính chất nào sau đây?
Bài 10 trang 73 sách bài tập Toán 8 Tập 1: Tính độ dài cạnh chưa biết của các tam giác vuông trong Hình 1.
Bài 11 trang 73 sách bài tập Toán 8 Tập 1: Tìm số đo các góc chưa biết của các tứ giác trong Hình 2.
Bài 12 trang 74 sách bài tập Toán 8 Tập 1: Cho tứ giác EKIT có EK = ET, IK = IT; . Gọi S là giao điểm của hai đường chéo. Tìm số đo các góc .
Bài 13 trang 74 sách bài tập Toán 8 Tập 1: Tính chiều cao của hình thang cân ABCD biết rằng cạnh bên BC = 25 cm và các cạnh đáy AB = 10 cm, CD = 24 cm.
Bài 14 trang 74 sách bài tập Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD, DB là tia phân giác của góc D, DB ⊥ BC. Biết AB = 4 cm. Tính chu vi hình thang đó.
Bài 15 trang 74 sách bài tập Toán 8 Tập 1: Cho tam giác ABC cân tại A có BC = 6 cm. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC.
Bài 16 trang 74 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho BM = DN.
Bài 17 trang 74 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Lấy các điểm M, N, P, Q lần lượt là trung điểm của AO, BO, CO, DO.
Bài 18 trang 74 sách bài tập Toán 8 Tập 1: Cho hình chữ nhật ABCD có AB = 2BC. Gọi I là trung điểm của AB và K là trung điểm của CD. Chứng minh:
Bài 19 trang 74 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi DE, BK lần lượt là đường phân giác của hai góc (E ∈ AB, K ∈ CD).
Xem thêm các bài giải sách bài tậpToán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Bài tập cuối chương 2
Bài 1: Định lí Pythagore
Bài 2: Tứ giác
Bài 3: Hình thang – Hình thang cân
Bài 5: Hình chữ nhật – Hình vuông
