Toptailieu.vn xin giới thiệu 05 câu trắc nghiệm Bài tập cuối chương 2 Kết nối tri thức (có đáp án 2023) CHỌN LỌC, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
05 câu trắc nghiệm Bài tập cuối chương 2 Kết nối tri thức (có đáp án 2023) CHỌN LỌC
Lý thuyết
1. Bất phương trình bậc nhất hai ẩn
• Bất phương trình bậc nhất hai ẩn x, y là bất phương trình có một trong các dạng sau:
ax + by < c; ax + by > c
ax + by ≤ c; ax + by ≥ c
trong đó: x, y là các ẩn,
a, b, c là các số cho trước (tham số) với a, b không đồng thời bằng 0.
• Cho bất phương trình bậc nhất hai ẩn ax + by < c (*).
Mỗi cặp số (x0; y0) sao cho ax0 + by0 < c gọi là một nghiệm của bất phương trình (*).
Trong mặt phẳng toạ độ Oxy, tập hợp các điểm có toạ độ là nghiệm của bất phương trình (*) được gọi là miền nghiệm của bất phương trình đó.
Nghiệm và miền nghiệm của các bất phương trình dạng ax + by > c; ax + by ≤ c và ax + by ≥ c được định nghĩa tương tự.
• Trong mặt phẳng toạ độ Oxy, đường thẳng d: ax + by = c chia mặt phẳng thành hai nửa mặt phẳng. Một trong hai nửa mặt phẳng (không kể d) là miền nghiệm của bất phương trình ax + by < c, nửa mặt phẳng còn lại (không kể d) là miền nghiệm của bất phương trình ax + by > c.
• Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn:
Bước 1. Vẽ đường thẳng d: ax + by = c. Đường thẳng d chia mặt phẳng toạ độ thành hai nửa mặt phẳng.
Bước 2. Lấy một điểm M(x0; y0) không nằm trên d (thường lấy gốc toạ độ O nếu c ≠ 0). Tính ax0 + by0 và so sánh với c.
Bước 3. Kết luận:
+ Nếu ax0 + by0 < c thì nửa mặt phẳng chứa điểm M (không kể d) là miền nghiệm của bất phương trình ax + by < c.
+ Nếu ax0 + by0 > c thì nửa mặt phẳng chứa điểm M (không kể d) là miền nghiệm của bất phương trình ax + by > c.
2. Hệ bất phương trình bậc nhất hai ẩn
• Hệ bất phương trình bậc nhất hai ẩn x, y là một hệ gồm một số bất phương trình bậc nhất hai ẩn x, y. Mỗi nghiệm chung của các bất phương trình trong hệ được gọi là một nghiệm của hệ bất phương trình đó.
• Miền nghiệm của hệ bất phương trình là giao của các miền nghiệm của các bất phương trình trong hệ.
• Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn:
+ Trong cùng mặt phẳng toạ độ, biểu diễn miền nghiệm của mỗi bất phương trình trong hệ bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.
+ Phần không bị gạch sau cùng là miền nghiệm cần tìm.
• Giá trị lớn nhất (hoặc nhỏ nhất) của biểu thức bậc nhất F(x , y) = ax + by trong miền đa giác A1A2…An là giá trị của F(x , y) tại một trong các đỉnh của đa giác đó.
Bài tập
Câu 1. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A. x + y > 3 B. x2+y2≤4
C. (x–y)(3x+y)≥1 D. y3−2≤0
Hướng dẫn giải:
Đáp án A
Câu 2. Cho bất phương trình 2x + y > 3. Khẳng định nào sau đây là đúng?
A. Bất phương trình đã cho có nghiệm duy nhất.
B. Bất phương trình đã cho vô nghiệm.
C. Bất phương trình đã cho có vô số nghiệm
D. Bất phương trình đã cho có tập nghiệm là [3;+∞).
Hướng dẫn giải:
Đáp án C
Câu 3. Hình nào sau đây biểu diễn miền nghiệm của bất phương trình x – y < 3?
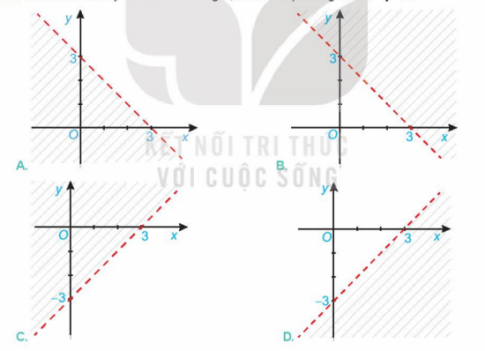
Hướng dẫn giải:
Đáp án D
Câu 4. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
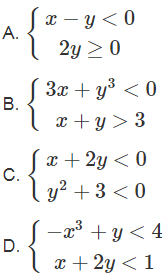
Hướng dẫn giải:
Đáp án A
Câu 5. Cho hệ bất phương trình 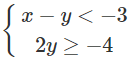 . Điểm nào sau đây thuộc miền nghiệm của hệ đã cho?
. Điểm nào sau đây thuộc miền nghiệm của hệ đã cho?
A. (0; 0) B. (-2; 1) C. (3; -1) D. (-3; 1)
Hướng dẫn giải:
Đáp án D
Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 4: Hệ bất phương trình bậc nhất hai ẩn
Bài 5: Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.