Toptailieu.vn xin giới thiệu 12 câu trắc nghiệm Bài tập cuối chương 5 Kết nối tri thức (có đáp án 2023) CHỌN LỌC, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

12 câu trắc nghiệm Bài tập cuối chương 5 Kết nối tri thức (có đáp án 2023) CHỌN LỌC

Lý thuyết

1. Số gần đúng

Trong nhiều trường hợp, ta không biết hoặc khó biết số đúng (kí hiệu là ) mà chỉ tìm được giá trị xấp xỉ nó. Giá trị này được gọi là số gần đúng, kí hiệu là a.

Chú ý:

Ta có thể sử dụng máy tính cầm tay để tìm giá trị gần đúng của các biểu thức chứa các số vô tỉ như π, ,...

2. Sai số tuyệt đối và sai số tương đối

a) Sai số tuyệt đối

Giá trị Δ_a = (a - )phản ánh mức độ sai lệch giữa số đúng và số gần đúng a, được gọi là sai số tuyệt đối của số gần đúng a.

Chú ý:

+ Trên thực tế, nhiều khi ta không biết nên cũng không biết ∆_a. Tuy nhiên, ta có thể đánh giá được ∆_a không vượt quá một số dương d nào đó.

+ Nếu ∆_a ≤ d thì a – d ≤ ≤ a + d, khi đó ta viết = a ± d và hiểu là số đúng nằm trong đoạn [a – d; a + d]. Do đó d càng nhỏ thì a càng gần nên d được gọi là độ chính xác của số gần đúng.

+ Trong các phép đo, độ chính xác d của số gần đúng bằng một nửa đơn vị của thước đo. Chẳng hạn, một thước đo có chia vạch đến xentimét thì mọi giá trị đo nằm giữa 6,5cm và 7,5cm đều được coi là 7cm. Vì vậy, thước đo có thang đo càng nhỏ thì cho giá trị đo càng chính xác.

b) Sai số tương đối

Sai số tương đối của số gần đúng a, kí hiệu là δa, là tỉ số giữa sai số tuyệt đối và |a|, tức là .

3. Quy tròn số gần đúng

Số thu được sau khi thực hiện làm tròn số được gọi là số quy tròn. Số quy tròn là một số gần đúng của số ban đầu.

Chú ý:

•Đối với chữ số hàng làm tròn:

+ Giữ nguyên nếu chữ số ngay bên phải nó nhỏ hơn 5;

+ Tăng 1 đơn vị nếu chữ số ngay bên phải nó lớn hơn hoặc bằng 5.

•Đối với chữ số sau hàng làm tròn:

+ Bỏ đi nếu ở phần thập phân;

+ Thay bởi các chữ số 0 nếu ở phần số nguyên.

Nhận xét:

+ Khi thay số đúng bởi số quy tròn đến một hàng nào đó thì sai số tuyệt đối của số quy tròn không vượt quá nửa đơn vị của hàng làm tròn.

+ Cho số gần đúng a với độ chính xác d. Khi được yêu cầu làm tròn số a mà không nói rõ làm tròn đến hàng nào thì ta làm tròn số a đến hàng thấp nhất mà d nhỏ hơn 1 đơn vị của hàng đó.

4. Số trung bình và trung vị

a) Số trung bình

Số trung bình (số trung bình cộng) của mẫu số liệu x₁, x₂,..., x_n, kí hiệu là được tính bằng công thức:

Chú ý:

Trong trường hợp mẫu số liệu cho dưới dạng bảng tần số thì số trung bình được tính theo công thức:

trong đó m_k là tần số của giá trị x_k và n = m₁ + m₂ +...+ m_k.

Ý nghĩa: Số trung bình là giá trị trung bình cộng của các số trong mẫu số liệu, nó cho biết vị trí trung tâm của mẫu số liệu và có thể dùng để đại diện cho mẫu số liệu.

b) Trung vị

Trong trường hợp mẫu số liệu có giá trị bất thường (rất lớn hoặc rất bé so với đa số các giá trị khác), người ta không dùng số trung bình để đo xu thế trung tâm mà dùng trung vị.

Để tìm trung vị (kí hiệu là Me) của một mẫu số liệu, ta thực hiện như sau:

+ Sắp xếp các giá trị trong mẫu số liệu theo thứ tự không giảm.

+ Nếu số giá trị của mẫu số liệu là số lẻ thì giá trị chính giữa của mẫu là trung vị. Nếu là số chẵn thì trung vị là trung bình cộng của hai giá trị chính giữa của mẫu.

Ý nghĩa: Trung vị không bị ảnh hưởng bởi giá trị bất thường trong khi số trung bình bị ảnh hưởng bởi giá trị bất thường. Vì vậy, khi mẫu số liệu có giá trị bất thường, người ta thường dùng trung vị đại diện cho các số liệu thống kê.

5. Tứ phân vị

Tứ phân vị dùng để xác định ngưỡng để phân loại các số liệu có trong mẫu số liệu.

Để tìm các tứ phân vị của mẫu số liệu có n giá trị, ta làm như sau:

+ Sắp xếp mẫu số liệu theo thứ tự không giảm.

+ Tìm trung vị. Giá trị này là Q₂.

+ Tìm trung vị của nửa số liệu bên trái Q₂ (không bao gồm Q₂ nếu n lẻ). Giá trị này là Q₁.

+ Tìm trung vị của nửa số liệu bên phải Q₂ (không bao gồm Q₂ nếu n lẻ). Giá trị này là Q₃.

Q₁, Q₂, Q₃ được gọi là các tứ phân vị của mẫu số liệu.

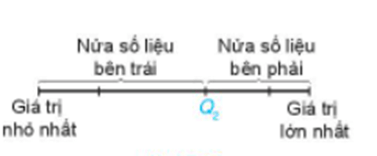
Chú ý: Q₁ được gọi là tứ phân vị thứ nhất hay tứ phân vị dưới, Q₃ được gọi là tứ phân vị thứ ba hay tứ phân vị trên.

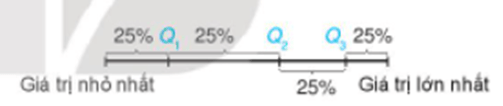
Ý nghĩa: Các điểm Q₁, Q₂, Q₃ chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành bốn phần, mỗi phần đều chứa 25% giá trị.

6. Mốt

Mốt của mẫu số liệu là giá trị xuất hiện với tần số lớn nhất.

Ý nghĩa: Có thể dùng mốt để đo xu thế trung tâm của mẫu số liệu khi mẫu số liệu có nhiều giá trị trùng nhau.

Nhận xét:

+ Mốt có thể không là duy nhất. Chẳng hạn, với mẫu số liệu sau:

6959975595

Ta thấy các số 5; 9 đều xuất hiện với số lần lớn nhất (4 lần) nên mẫu số liệu này có hai mốt là 5 và 9.

+ Khi các giá trị trong mẫu số liệu xuất hiện với tần số như nhau thì mẫu số liệu không có mốt. Chẳng hạn, với mẫu số liệu sau:

686786778

Ta thấy các giá trị 6; 7; 8 trong mẫu số liệu đều xuất hiện với tần số như nhau (3 lần) nên mẫu số liệu này không có mốt.

+ Mốt còn được định nghĩa cho mẫu dữ liệu định tính (dữ liệu không phải là số). Ví dụ trong buổi biểu quyết chọn một trong ba bạn Hoa, Bình, Tú làm bí thư của lớp 10C, bạn thư ký của lớp đã tổng kết được kết quả biểu quyết như sau:

Trong mẫu dữ liệu này, số phiếu chọn “bạn Hoa” nhiều nhất, được gọi là mốt.

7. Khoảng biến thiên và khoảng tứ phân vị

a) Khoảng biến thiên

Khoảng biến thiên, kí hiệu là R, là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất trong mẫu số liệu.

Ý nghĩa: Khoảng biến thiên dùng để đo độ phân tán của mẫu số liệu. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán.

Nhận xét: Sử dụng khoảng biến thiên có ưu điểm là đơn giản, dễ tính toán song khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và giá trị nhỏ nhất mà bỏ qua thông tin từ tất cả các giá trị khác. Do đó, khoảng biến thiên rất dễ bị ảnh hưởng bởi các giá trị bất thường.

b) Khoảng tứ phân vị

Khoảng tứ phân vị, kí hiệu là ∆_Q, là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất, tức là:

∆_Q = Q₃ – Q₁.

Về bản chất, khoảng tứ phân vị là khoảng biến thiên của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp.

Ý nghĩa: Khoảng tứ phân vị cũng là một số đo độ phân tán của mẫu số liệu. Khoảng tứ phân vị càng lớn thì mẫu số liệu càng phân tán.

Chú ý: Một số tài liệu gọi khoảng biến thiên là biên độ và khoảng tứ phân vị là độ trải giữa.

8. Phương sai và độ lệch chuẩn

Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu (bỏ qua thông tin của tất cả các giá trị khác). Khoảng tứ phân vị chỉ sử dụng thông tin của 50% số liệu chính giữa. Có một vài số đặc trưng khác đo độ phân tán sử dụng thông tin của tất cả các giá trị trong mẫu số liệu. Hai trong số đó là phương sai và độ lệch chuẩn.

Cụ thể với mẫu số liệu x₁, x₂,..., x_n, nếu gọi số trung bình là  thì với mỗi giá trị x_i, độ lệch của nó so với giá trị trung bình là x_i – .

•Phương sai là giá trị .

•Căn bậc hai của phương sai, s = , được gọi là độ lệch chuẩn.

Chú ý: Người ta còn sử dụng đại lượng để đo độ phân tán của mẫu số liệu:

.

Ý nghĩa: Nếu số liệu càng phân tán thì phương sai và độ lệch chuẩn càng lớn.

9. Phát hiện số liệu bất thường hoặc không chính xác bằng biểu đồ hộp

Trong mẫu số liệu thống kê, có khi ta sẽ gặp phải những giá trị quá lớn hoặc quá nhỏ so với đa số các giá trị khác. Những giá trị này được gọi là giá trị bất thường. Chúng xuất hiện trong mẫu số liệu có thể do nhầm lẫn hay sai sót nào đó. Ta có thể dùng biểu đồ hộp để phát hiện những giá trị bất thường này.

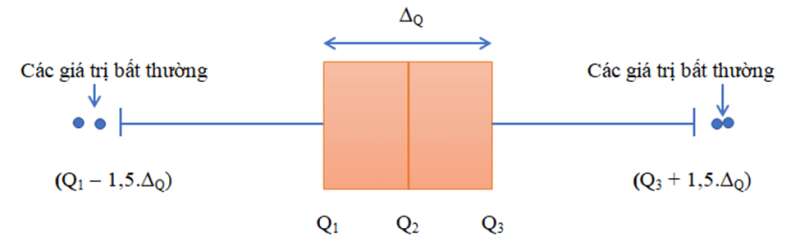
Các giá trị lớn hơn Q₃ + 1,5 . ∆_Q hoặc bé hơn Q₁ – 1,5 . ∆_Q được xem là giá trị bất thường.

Bài tập

Bài 1: Số quy tròn của số gần đúng 167,23 ± 0,07 là

A. 167,23;

B. 167,2;

C. 167,3;

D. 167.

Lời giải:

Đáp án đúng là: B

Ta có số gần đúng a = 167,23 với độ chính xác d = 0,07.

Vì d = 0,07 nên ta quy tròn số 167,23 đến hàng phần mười.

Vậy số quy tròn của a là 167,2.

Ta chọn phương án B.

Bài 2: Biết độ ẩm không khí tại Hà Nội là 51% ± 2%. Khi đó

A. Sai số tuyệt đối δ = 2%;

B. Sai số tuyệt đối δ = 1%;

C. Độ chính xác d = 2%;

D. Độ chính xác d = 1%.

Lời giải:

Đáp án đúng là: C

Ta có số gần đúng a = 51% với độ chính xác d = 2%.

Khi đó sai số tuyệt đối D_a ≤ d = 2%.

Ta chọn phương án C.

Bài 3: Một học sinh thực hành đo chiều cao của một toà tháp cho kết quả là 200 m. Biết chiều cao thực của toà tháp là 201 m, sai số tương đối là

A. 0,5%;

B. 1%;

C. 2%;

D. 4%.

Lời giải:

Đáp án đúng là: A

Ta có số đúng là  = 201 m và số gần đúng là a = 200 m.

Khi đó D_a = |a – | = |200 – 201| = 1 m.

Sai số tương đối của số gần đúng a là:

 = 0,5%

Ta chọn phương án A.

Bài 4: Điểm thi học kì môn Toán của một nhóm bạn như sau:

8        9        7        10      7        5        7        8.

Mốt của mẫu số liệu trên là

A. 5;

B. 7;

C. 8;

D. 9.

Lời giải:

Đáp án đúng là: B

Ta thấy điểm 7 có nhiều bạn nhất nên mốt của mẫu số liệu trên là 7.

Ta chọn phương án B.

Bài 5: Trung vị của mẫu số liệu trong Bài 5.22 là

A. 6;

B. 7;

C. 7,5;

D. 8.

Lời giải:

Đáp án đúng là: C

Sắp xếp mẫu số liệu theo thứ tự không giảm ta được:

5        7        7        7        8        8        9        10.

Vì n = 8 là số chẵn nên trung vị của dãy số liệu trên là trung bình cộng của hai giá trị chính giữa (số liệu thứ 4 và thứ 5) của mẫu đã sắp xếp.

Do đó Me =  =7,57 5

Ta chọn phương án C.

Bài 6: Bổ sung thêm số 9 vào mẫu số liệu trong Bài 5.22 thì trung vị của mẫu số liệu mới là

A. 6;

B. 7;

C. 7,5;

D. 8.

Lời giải:

Đáp án đúng là: D

Bổ sung số 9 vào mẫu số liệu ban đầu và sắp xếp mẫu số liệu mới theo thứ tự không giảm ta được:

5        7        7        7        8        8        9        9        10.

Vì n = 9 là số lẻ nên trung vị của dãy số liệu trên là giá trị chính giữa (số liệu thứ 5) của mẫu đã sắp xếp.

Do đó Me = 8.

Ta chọn phương án D.

Bài 7: Cho mẫu số liệu sau:

156    158    160    162    164.

Nếu bổ sung hai giá trị 154, 167 vào mẫu số liệu này thì so với mẫu số liệu ban đầu:

A. Trung vị và số trung bình đều không thay đổi;

B. Trung vị thay đổi, số trung bình không thay đổi;

C. Trung vị không thay đổi, số trung bình thay đổi;

D. Trung vị và số trung bình đều thay đổi.

Lời giải:

Đáp án đúng là: C

– Xét dãy dữ liệu ban đầu:

156    158    160    162    164.

• Số trung bình là:

 = 160

• Vì n = 5 là số lẻ nên trung vị của mẫu số liệu là giá trị chính giữa (số liệu thứ 3) của mẫu số liệu đã sắp xếp.

Do đó Me = 160.

– Bổ sung hai giá trị 154, 167 vào mẫu số liệu ban đầu và sắp xếp mẫu số liệu mới theo thứ tự không giảm ta được:

154    156    158    160    162    164    167.

• Số trung bình là:

x =   ≈ 160,14.

• Vì n = 7 là số lẻ nên trung vị của mẫu số liệu là giá trị chính giữa (số liệu thứ 4) của mẫu số liệu đã sắp xếp.

Do đó Me = 160.

Vậy nếu bổ sung hai giá trị 154, 167 vào mẫu số liệu này thì so với mẫu số liệu ban đầu:

Trung vị không thay đổi, số trung bình thay đổi.

Ta chọn phương án C.

Bài 8: Cho mẫu số liệu sau:

156    158    160    162    164.

Tứ phân vị thứ nhất của mẫu số liệu trên là

A. 156;

B. 157;

C. 158;

D. 159.

Lời giải:

Đáp án đúng là: B

Xét mẫu số liệu:

156    158    160    162    164.

• Vì n = 5 là số lẻ nên trung vị của mẫu số liệu là giá trị chính giữa (số liệu thứ 3) của mẫu số liệu đã sắp xếp.

Do đó Q₂ = 160.

• Nửa số liệu bên trái Q₂ là: 156; 158.

Dãy này gồm 2 số liệu, n = 2 là số chẵn nên trung vị là trung bình cộng của hai giá trị.

Do đó Q₁ = 156+1582=157.156+1582=157.

Vậy tứ phân vị thứ nhất của mẫu số liệu đã cho là Q₁ = 157.

Ta chọn phương án B.

Bài 9: Mẫu số liệu trong Bài 5.26 có khoảng biến thiên là

A. 2;

B. 4;

C. 6;

D. 8.

Lời giải:

Đáp án đúng là: D

Xét mẫu số liệu:

156    158    160    162    164.

Giá trị thấp nhất, cao nhất tương ứng là 156; 164.

Khoảng biến thiên của mẫu số liệu trên là:

R = 164 – 156 = 8.

Ta chọn phương án D.

Bài 10: Mẫu số liệu mà tất cả các số trong mẫu này bằng nhau có phương sai là

A. –1;

B. 0;

C. 1;

D. 2.

Lời giải:

Đáp án đúng là: B

Giả sử mẫu số liệu x₁, x₂, … , x_n có x₁ = x₂ = … = x_n = x

Khi đó:

• Số trung bình là:  x.

• Phương sai là:

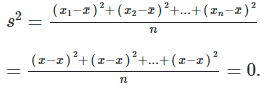
Ta chọn phương án B.

Bài 11: Số giá trị trong mẫu số liệu nhỏ hơn tứ phân vị dưới Q1 chiếm khoảng

A. 25% số giá trị của dãy;

B. 50% số giá trị của dãy;

C. 75% số giá trị của dãy;

D. 100% số giá trị của dãy.

Lời giải:

Đáp án đúng là: A

Số giá trị trong mẫu số liệu nhỏ hơn tứ phân vị dưới Q₁ chiếm khoảng 25% số giá trị của dãy.

Ta chọn phương án A.

Bài 12: Khoảng tứ phân vị D_Q là

A. Q₂ – Q₁;

B. Q₃ – Q₁;

C. Q₃ – Q₂;

D. (Q₁ + Q₁) : 2.

Lời giải:

Đáp án đúng là: B

Khoảng tứ phân vị D_Q là: D_Q = Q₃ – Q₁.

Ta chọn phương án B.

Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 14: Các số đặc trưng đo độ phân tán

Tìm hiểu một số kiến thức về tài chính

Mạng xã hội: Lợi và hại

Bài 15: Hàm số

Bài 16: Hàm số bậc hai