Toptailieu.vn xin giới thiệu 15 câu trắc nghiệm Các số đặc trưng đo xu thế trung tâm Kết nối tri thức (có đáp án 2023) CHỌN LỌC, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

15 câu trắc nghiệm Các số đặc trưng đo xu thế trung tâm Kết nối tri thức (có đáp án 2023) CHỌN LỌC

Lý thuyết

1. SỐ TRUNG BÌNH VÀ TRUNG VỊ

a. Số trung bình

Cho mẫu số liệu x₁, x₂, x₃, ..., x_n

+) Số trung bình (hay TB cộng) của mẫu số liệu kí hiệu là , được tính bằng công thức: 

+) Mẫu số liệu cho dưới dạng bảng tần số thì:

Với m_i là tần số của giá trị x_i và n = m₁ + m₂ + ... + m_k

+) Ý nghĩa: Số trung bình là giá trị trung bình cộng, cho biết vị trí trung tâm của mẫu số liệu và có thể dùng để đại diện cho mẫu số liệu

b. Trung vị

+) Trong trường hợp mẫu số liệu có giá trị bất thường (rất lớn hoặc rất bé so với đa số các giá trị khác), ta dùng trung vị để đo xu thế trung tâm.

Ví dụ: mẫu số liệu: 1      3       2        3         4         20

 Tìm trung vị:

Bước 1: Sắp xếp các giá trị theo thứ tự không giảm X₁, X₂,..., X_n

Bước 2: Cỡ mẫu = n.

  + Nếu n lẻ (n = 2k - 1) thì trung vị là X_k

  + Nếu n chẵn (n = 2k) thì trung vị bằng (X_k + X_k+1)

+) Ý nghĩa: Trung vị là giá trị ở vị trí chính giữa của mẫu số liệu đã sắp xếp theo thứ tự không giảm. Trung vị không bị ảnh hưởng bởi giá trị bất thường như số trung bình.

2. TỨ PHÂN VỊ

Tứ phân vị gồm 3 giá trị Q₁, Q₂, Q₃, nó chia mẫu số liệu đã sắp xếp

theo thứ tự từ nhỏ đến lớn thành 4 phần, mỗi phần đều chứa 25% giá trị.

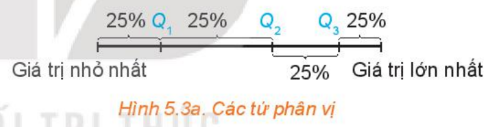
+) Các bước tìm tứ phân vị:

Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm.

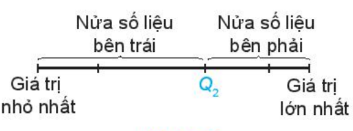
Bước 2: Tìm trung vị, chính là Q₂

Bước 3: Q₁ là trung vị của nửa số liệu bên trái Q₂ (không bao gồm Q₂ nếu n lẻ).

Bước 4: Q₃ là trung vị của nửa số liệu bên phải Q₂ (không bao gồm Q₂ nếu n lẻ).

Chú ý:

Q1 còn được gọi là tứ phân vị thứ nhất hoặc tứ phân vị dưới.

Q3 còn được gọi là tứ phân vị thứ ba hoặc tứ phân vị trên.

3. MỐT

+) Mốt của mẫu số liệu là giá trị xuất hiện với tần số lớn nhất

+) Ý nghĩa: Dùng mốt để đo xu thế trung tâm của mẫu số liệu khi mẫu có nhiều giá trị trùng nhau.

+) Nhận xét

  - Mốt có thể không là duy nhất. Một mẫu có thể có nhiều mốt

  - Khi các giá trị trong mẫu xuất hiện với tần số như nhau thì mẫu số liệu đó không có mốt.

Bài tập

Câu 1. Một xạ thủ bắn 30 viên đạn vào bia kết quả được ghi lại trong bảng phân bố như sau

Khi đó điểm trung bình cộng là (kết quả làm tròn đến hàng phần trăm)

A. 8,33;

B. 8,34;

C. 8,31;

D. 8,32.

Đáp án: A

Ta có x =  = 8,33 3333333…

Điểm trung bình cộng làm tròn đến hàng phần trăm là 8,33.

Câu 2. Điểm kiểm tra môn Toán của 10 học sinh được cho như sau 6; 7; 7; 6; 7; 8; 8; 7; 9; 9. Số trung vị của mẫu số liệu trên là

A. 6;

B. 7;

C. 8;

D. 9.

Đáp án: B

Ta sắp xếp số liệu theo thứ tự không giảm như sau: 6; 6; 7; 7; 7; 7; 8; 8; 9; 9.

Dãy số trên có tất cả 10 giá trị, 2 giá trị chính giữa bằng 7. Vậy số trung vị của mẫu số liệu trên là (7 + 7):2 = 7.

Câu 3. Cho mẫu số liệu thống kê: 5; 2; 1; 6; 7; 5; 4; 5; 9. Mốt của mẫu số liệu trên bằng

A. 6;

B. 7;

C. 5;

D. 9.

Đáp án: C

Ta có giá trị 5 xuất hiện nhiều nhất trong mẫu số liệu trên. Vậy mốt bằng 5

Câu 4. Điểm thi học kỳ 11 môn của một học sinh như sau: 4; 6; 5; 7; 5; 5; 9; 8; 7; 10; 9. Số trung bình và trung vị lần lượt là

A. 6 và 5;

B. 6, 52 và 5;

C. 6,73 và 7;

D. 6,81 và 7.

Đáp án: D

Ta có  = 6,81 

Sắp xếp số theo thứ tự không giảm 4; 5; 5; 5; 6; 7; 7; 8; 9; 9; 10. Dãy số liệu có tất cả 11 giá trị là số lẻ nên ta có số chính giữa của dãy số liệu có giá trị bằng 7, nên số trung vị là 7.

Câu 5. Giá của một loại quần áo (đơn vị nghìn đồng) cho bởi số liệu như sau: 350; 300; 350; 400; 450; 400; 450; 350; 350; 400. Tứ phân vị của số liệu là

A. Q₁ = 350; Q₂ = 375; Q₃ = 400;

B. Q₁ = 350; Q₂ = 400; Q₃ = 400;

C. Q₁ = 300; Q₂ = 375; Q₃ = 400;

D. Q₁ = 350; Q₂ = 400; Q₃ = 350.

Đáp án: A

Sắp xếp số liệu theo thứ tự không giảm 300; 350; 350; 350; 350; 400; 400; 400; 450; 450.

Vì n = 10 là số chẵn nên Q₂ là trung bình cộng của hai số chính giữa

Q₂ = (350 + 400) : 2 = 375.

Ta tìm Q₁ là trung vị nửa số liệu bên trái của Q₂ là 300; 350; 350; 350; 350 gồm 5 giá trị và tìm được Q₁ = 350.

Ta tìm Q₃ là trung vị nửa số liệu bên phải của Q₂ là 400; 400; 400; 450; 450 gồm 5 giá trị và tìm được Q₃ = 400.

Vậy tứ phân vị của mẫu số liệu là: Q₁ = 350; Q₂ = 375; Q₃ = 400;

Câu 6. Số đo cỡ áo của 10 học sinh lớp 9 được cho bởi số liệu sau: 36; 37; 38; 36; 36; 38; 37; 39; 37; 38. Tứ phân vị của số liệu là

A. Q₁ = 36; Q₂ = 37; Q₃ = 38;

B. Q₁ = 37; Q₂ = 36; Q₃ = 38;

C. Q₁ = 36; Q₂ = 38; Q₃ = 37;

D. Q₁ = 37; Q₂ = 38; Q₃ = 39.

Đáp án: A

Sắp xếp số liệu theo thứ tự không giảm 36; 36; 36; 37; 37; 37; 38; 38; 38; 39.

Vì n = 10 là số chẵn nên Q₂ là trung bình cộng của hai số chính giữa

Q₂ = (37 + 37) : 2 = 37

Ta tìm Q₁ là trung vị nửa số liệu bên trái của Q₂ là 36; 36; 36; 37; 37 gồm 5 giá trị và tìm được Q₁ = 36

Ta tìm Q₃ là trung vị nửa số liệu bên phải của Q₂ là 37; 38; 38; 38; 39 gồm 5 giá trị và tìm được Q₃ = 38.

Vậy tứ phân vị của số liệu là Q₁ = 36; Q₂ = 37; Q₃ = 38.

Câu 7. Điểm toán cuối năm của một nhóm 9 học sinh lớp 6 là 5; 5; 3; 6; 7; 7; 8; 8; 9. Điểm trung bình của cả nhóm là

A. 6,44;

B. 7;

C. 7,11;

D. 8,1.

Đáp án: A

Ta có   ≈ 6,44.

Vậy điểm trung bình của cả nhóm là 6,44.

Câu 8. Khối lượng 20 củ khoai tây thu hoạch tại nông trường được ghi lại như sau: 90; 73; 88; 99; 100; 102; 111; 96; 79; 93; 81; 94; 96; 93; 93; 95; 82; 90; 106; 103 (đơn vị: gam). Tứ phân vị của số liệu là

A. Q₁ = 88; Q₂ = 93; Q₃ = 99;

B. Q₁ = 88; Q₂ = 93,5; Q₃ = 99,5;

C. Q₁ = 89; Q₂ = 93; Q₃ = 99;

D. Q₁ = 89; Q₂ = 93,5; Q₃ = 99,5.

Đáp án: D

Sắp xếp số liệu theo thứ tự không giảm 73; 79; 81; 82; 88; 90; 90; 93; 93; 93; 94; 95; 96; 96; 99; 100; 102; 103; 106; 111

Vì n = 20 là số chẵn nên Q₂ là trung bình cộng của hai số chính giữa

Q₂ = (93 + 94) : 2 = 93,5

Ta tìm Q₁ là trung vị nửa số liệu bên trái của Q₂ là 73; 79; 81; 82; 88; 90; 90; 93; 93; 93 gồm 10 giá trị, hai số chính giữa là 88. 90. Do đó Q₁ = (88 + 90) : 2 = 89

Ta tìm Q₃ là trung vị nửa số liệu bên phải của Q₂ là 94; 95; 96; 96; 99; 100; 102; 103; 106; 111 gồm 10 giá trị, hai giá trị chính giữa là 99, 100, Do đó Q₃ = (99 + 100) : 2 = 99,5.

Vậy Q₁ = 89; Q₂ = 93,5; Q₃ = 99,5.

Câu 9. Tuổi thọ của 20 bóng đèn được thắp thử được ghi lại ở bảng số liệu sau (đơn vị: giờ)

Tuổi thọ trung bình của số bóng đèn trên là

A. 1173,5;

B. 1174,5;

C. 1175,5;

D. 1176,5.

Đáp án: B

Ta có  = 1174,5 

Câu 10. Tiền lương hàng tháng của 7 nhân viên trong một công ty du lịch là: 6,5; 8,4; 6,9; 7,2; 10; 6,7; 12 (đơn vị: triệu đồng). Tìm số trung vị của số liệu trên

A. 8,4;

B. 6,9;

C. 7,2;

D. 8.2.

Đáp án: C

Ta sắp xếp dãy số theo thứ tự không giảm như sau: 6,5; 6,7; 6,9; 7,2; 8,4; 10; 12

Dãy số trên có tất cả 7 giá trị nên số trung vị là giá trị chính giữa của số liệu bằng 7,2.

Vậy số trung vị của mẫu số liệu bằng Q₂ = 7,2.

Câu 11. Năng xuất lúa của 3 hộ gia đình tại xã A như sau

Năng xuất lúa trung bình của toàn bộ 3 hộ gia đình trên là

A. 38;

B. 37,6;

C. 38,5;

D. 39.

Đáp án: B

Tổng sản lượng lúa thu hoạch được của cả 3 hộ gia đình là: 376 (tạ)

Năng xuất lúa trung bình của toàn bộ 3 hộ gia đình trên là:  = 37,6 (tạ/ha)

Cây 12. Giá trị thành phẩm quy ra tiền (nghìn đồng) trong một tuần lao động của 7 công nhân trong một công ty là: 180; 200; 210; 190; 210; 190; 220. Mốt của mẫu số liệu trên là

A. 210;

B. 220;

C. 190, 210;

D. 180, 220.

Đáp án: C

Ta thấy trong mẫu số liệu giá trị thành phẩm quy ra tiền của công nhân có 190 và 210 xuất hiện nhiều nhất (2 lần). Vậy mốt của mẫu số liệu là 190, 210.

Câu 13. Khối lượng 10 con cá chép bất kỳ trong hồ được thống kê bởi mẫu số liệu sau: 640; 645; 650; 650; 645; 650; 650; 645; 650; 640 (đơn vị: gam). Khối lượng trung bình của 10 con cá chép trong mẫu số liệu trên là

A. 650;

B. 645;

C. 646,5;

D. 645,5.

Đáp án: C

Ta có  = 646,5 .

Vậy khối lượng trung bình của 10 con cá chép trong mẫu số liệu trên là 646,5 kg.

Câu 14. Tiền thưởng của 20 công nhân trong một công ty được thống kê bởi mẫu số liệu: 3; 2; 4; 4; 5; 4; 3; 4; 5; 3; 5; 2; 2; 4; 5; 4; 3; 5; 4; 5 (đơn vị: triệu đồng). Tứ phân vị của mẫu số liệu là

A. Q₁ = 2; Q₂ = 4; Q₃ = 5;

B. Q₁ = 3; Q₂ = 3; Q₃ = 5;

C. Q₁1 = 2; Q₂ = 3; Q₃ = 4;

D. Q₁ = 3; Q₂ = 4; Q₃ = 5.

Đáp án: D

Sắp xếp mẫu số liệu theo thứ tự không giảm 2; 2; 2; 3; 3; 3; 3; 4; 4; 4; 4; 4; 4; 4; 5; 5; 5; 5; 5; 5.

Vì n = 20 là số chẵn nên Q₂ là trung bình cộng của hai số chính giữa

Q₂ = (4 + 4) : 2 = 4

Ta tìm Q₁ là trung vị nửa số liệu bên trái của Q₂ là 2; 2; 2; 3; 3; 3; 3; 4; 4; 4 gồm 10 giá trị, hai số chính giữa là 3 và 3. Do đó Q₁ = (3 + 3) : 2 = 3

Ta tìm Q₃ là trung vị nửa số liệu bên phải của Q₂ là 4; 4; 4; 4; 5; 5; 5; 5; 5; 5 gồm 10 giá trị, hai giá trị chính giữa là 5 và 5. Do đó Q₃ = (5 + 5) : 2 = 5.

Vậy tứ phân vị của mẫu số liệu Q₁ = 3; Q₂ = 4; Q₃ = 5

Câu 15. Ba nhóm học sinh gồm 10 người, 15 người, 25 người. khối lượng trung bình của mỗi nhóm là 50 kg; 45 kg; 40 kg. Khối lượng trung bình của cả ba nhóm là

A. 45 kg;

B. 43,5 kg;

C. 40,5 kg;

D. 42,5 kg.

Đáp án:

Tổng khối lượng của 3 nhóm học sinh là: 50.10 + 15.45 + 25.40 = 2170 (kg)

Khối lượng trung bình của cả ba nhóm học sinh là:  = 43,5 (kg).

Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 12: Số gần đúng và sai số

Bài 14: Các số đặc trưng đo độ phân tán

Bài tập cuối chương 5

Tìm hiểu một số kiến thức về tài chính

Mạng xã hội: Lợi và hại