Toptailieu.vn biên soạn và giới thiệu Lý thuyết Tập hợp ℚ các số hữu tỉ (Cánh Diều) Toán 7 hay, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững nội dung kiến thức từ đó dễ dàng làm các bài tập Toán 7.

Lý thuyết Tập hợp ℚ các số hữu tỉ (Cánh Diều) Toán 7

A. Lý thuyết

1. Số hữu tỉ

- Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}\left(a,b\in \mathbb{Z},b\ne 0\right)$ .

- Tập hợp các số hữu tỉ kí hiệu là ℚ.

Ví dụ: Các số $-7;\text{ 0,6; }-1,2;\text{ 1}\frac{4}{5}$ là các số hữu tỉ bởi vì chúng đều viết được dưới dạng phân số:  $-7=\frac{-7}{1}\text{; 0,6=}\frac{6}{10};-\text{1,2=}\frac{-12}{10};\text{ 1}\frac{4}{5}=\frac{9}{5}$.

Chú ý:

- Mỗi số nguyên là một số hữu tỉ.

- Các phân số bằng nhau là cách viết khác nhau của cùng một số hữu tỉ.

Ví dụ: Vì  $\frac{1}{2}=\frac{2}{4}$ nên $\frac{1}{2}$ và $\frac{2}{4}$cùng biểu diễn một số hữu tỉ.

2. Biểu diễn số hữu tỉ trên trục số

- Tương tự số nguyên ta có thể biểu diễn mọi số hữu tỉ trên trục số.

- Điểm biểu diễn số hữu tỉ a được gọi là điểm a.

- Do các phân số bằng nhau cùng biểu diễn một số hữu tỉ nên khi biểu diễn số hữu tỉ trên trục số ta chọn một trong những phân số đó để biểu diễn. Thông thường ta chọn phân số tối giản để biểu diễn số hữu tỉ đó.

- Nếu số hữu tỉ chưa viết dưới dạng phân số thì ta viết lại chúng dưới dạng phân số rồi biểu diễn phân số đó trên trục số.

Ví dụ: a) Biểu diễn số hữu tỉ 1,5 trên trục số.

- Ta viết 1,5 dưới dạng phân số: $1,5=\frac{15}{10}=\frac{3}{2}$. Ta sẽ biểu diễn phân số $\frac{3}{2}$ trên trục số.

- Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành hai phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng $\frac{1}{2}$ đơn vị cũ).

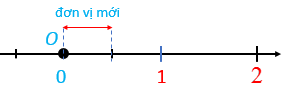
- Đi theo chiều dương của trục số bắt đầu từ điểm 0, ta lấy 3 đơn vị mới đến điểm M. Điểm M biểu diễn số hữu tỉ , và cũng chính là điểm biểu diễn số hữu tỉ 1,5 và $\frac{15}{10}$.

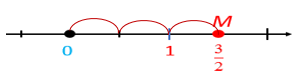b) Biểu diễn số hữu tỉ $\frac{-3}{2}$ trên trục số.

- Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành hai phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng $\frac{1}{2}$ đơn vị cũ).

- Đi theo chiều ngược chiều dương của trục số bắt đầu từ điểm 0, ta lấy 3 đơn vị mới đến điểm N. Điểm N biểu diễn số hữu tỉ 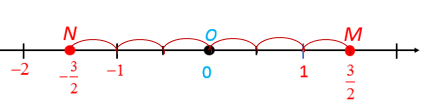$\frac{-3}{2}$.

Nhận xét: Vì $-\frac{3}{2}=\frac{-3}{2}=\frac{3}{-2}$ nên điểm N biểu diễn số $\frac{-3}{2}$ cũng là điểm biểu diễn số $\frac{-3}{2}$ và $\frac{3}{-2}$.

3. Số đối của một số hữu tỉ

- Trên trục số hai số hữu tỉ phân biệt có điểm biểu diễn nằm về hai phía của điểm gốc O và cách đều điểm gốc 0 được gọi là hai số đối nhau.

- Số đối của số hữu tỉ a, kí hiệu là –a.

- Số đối của số 0 là 0.

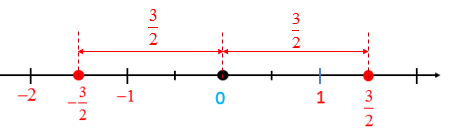Ví dụ:

- Số đối của số $\frac{3}{2}$ là số $-\frac{3}{2}$

- Số đối của số $\frac{-2}{7}$ là số $-\left(\frac{-2}{7}\right)=\frac{2}{7}$ .

4. So sánh các số hữu tỉ

4.1 So sánh hai số hữu tỉ

Trong hai số hữu tỉ khác nhau bao giờ cũng có một số nhỏ hơn số kia.

- Nếu số hữu tỉ a nhỏ hơn số hữu tỉ b thì ta viết a < b hay b > a

- Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.

- Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm.

- Số hữu tỉ 0 không là số hữu tỉ âm cũng không là số hữu tỉ dương

- Nếu a < b và  b < c thì a < c.

4.2 Cách so sánh hai số hữu tỉ

+ Khi hai số hữu tỉ cùng là phân số hoặc cùng là số thập phân, ta dùng quy tắc đã học ở lớp 6 để so sánh.

+ Các trường hợp khác hai trường hợp trên, để so sánh hai số hữu tỉ ta viết chúng cùng về dạng phân số (hoặc cùng dạng số thập phân) rồi so sánh chúng.

Ví dụ:

 a) So sánh $-\frac{1}{3}$ và $\frac{-2}{5}$

Hai phân số trên cùng là phân số, vì vậy ta sẽ áp dụng quy tắc so sánh hai phân số đã học.

Ta quy đồng để đưa hai phân số về cùng mẫu số dương

$-\frac{1}{3}=\frac{-1}{3}=\frac{(-1)\cdot 5}{3\cdot 5}=\frac{-5}{15}$;     $\frac{-2}{5}=\frac{(-2)\cdot 3}{5\cdot 3}=\frac{-6}{15}$     

Vì $-5>-6$ nên $\frac{-5}{15}>\frac{-6}{15}$. Suy ra $-\frac{1}{3}>\frac{-2}{5}$.

b) So sánh 1,206 và 1,3

Hai số trên cùng là số thập phân, vì vậy ta sẽ áp dụng quy tắc so sánh hai số thập phân.

Ta so sánh phần nguyên với nhau, khi phần nguyên bằng nhau ta sẽ so sánh đến phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn…

1,206 < 1,3 (vì phần nguyên bằng nhau, hàng phần mười có 2 < 3).

c) So sánh – 0,3 và $\frac{-2}{7}$

Ta thấy hai số trên chưa cùng là phân số hoặc số thập phân, vì vậy ta đưa chúng về cùng là phân số hoặc số thập phân sau đó so sánh chúng.

Ta có $-0,3=\frac{-3}{10}$, ta sẽ  áp dụng quy tắc so sánh hai phân số $\frac{-3}{10}$và $\frac{-2}{7}$

Ta có : $\frac{-3}{10}=\frac{(-3)\cdot 7}{10\cdot 7}=\frac{-21}{70}$;  $\frac{-2}{7}=\frac{(-2)\cdot 10}{7\cdot 10}=\frac{-20}{70}$   

Vì – 21 < –20 nên $\frac{-21}{70}<\frac{-20}{70}$. Suy ra – 0,3 < $\frac{-2}{7}$ .

4.3 Minh họa trên trục số

Hai điểm x, y lần lượt biểu diễn hai số hữu tỉ x, y trên trục số :

- Trên trục số nằm ngang: Nếu x < y hay y > x thì điểm x nằm bên trái điểm y.

- Trên trục số thẳng đứng: Nếu x < y hay y > x thì điểm x nằm phía dưới điểm y.

Ví dụ : So sánh hai số: – 2 và $\frac{-5}{3}$  

Ta có : $-2=\frac{-2}{1}=\frac{-6}{3}$ mà $\frac{-6}{3}<\frac{-5}{3}$ vậy nên $-2<\frac{-5}{3}$ .

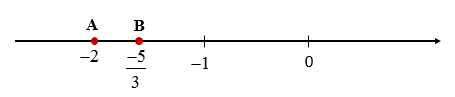Trên trục số nằm ngang điểm – 2 nằm bên trái điểm $\frac{-5}{3}$.

B. Bài tập tự luyện

B.1 Bài tập tự luận

Bài 1. Hãy biểu diễn số hữu tỉ $-\frac{3}{4}$ trên trục số.

Hướng dẫn giải

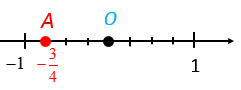
- Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành bốn phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng $\frac{1}{4}$ đơn vị cũ).

- Đi theo chiều ngược chiều dương của trục số bắt đầu từ điểm 0, ta lấy 3 đơn vị mới đến điểm A. Điểm A chính là điểm biểu diễn số hữu tỉ $-\frac{3}{4}$.

Bài 2. Các số: $-1,25;\text{ 0; 2}\frac{5}{7};$có là số hữu tỉ không? Vì sao?

Hướng dẫn giải

 Các số $-1,25;\text{ 0; 2}\frac{5}{7};$đều là số hữu tỉ, vì vậy chúng viết được dưới dạng phân số: $-1,25=\frac{-125}{100};\text{ 0=}\frac{0}{1}\text{; 2}\frac{5}{7}\text{=}\frac{19}{7}$ .

Bài 3. So sánh hai số hữu tỉ $\frac{2}{-7}$ và $\frac{-3}{11}$ .

Hướng dẫn giải

Hai số hữu tỉ trên đã viết dưới dạng phân số vì vậy để so sánh ta đưa phân số về có cùng mẫu dương, sau đó ta chỉ cần so sánh hai tử số.

Ta có $\frac{2}{-7}=\frac{-2}{7}=\frac{-22}{77}$ và $\frac{-3}{11}=\frac{-21}{77}$

Vì $-22<-21$ nên $\frac{-22}{77}<\frac{-21}{77}$ . Suy ra $\frac{2}{-7}$ < $\frac{-3}{11}$ .

Bài 4. Tìm số đối của số hữu tỉ $\frac{3}{-5}$ .

Hướng dẫn giải

Số đối của số hữu tỉ $\frac{3}{-5}$ là: $-\left(\frac{3}{-5}\right)=-\left(-\frac{3}{5}\right)=\frac{3}{5}$.

B.2 Bài tập trắc nghiệm

Câu 1. Chọn câu trả lời đúng?

A. –5 ∈ ℕ;

B. $-\frac{5}{7}\in \mathbb{Z}\text{;}$

C. $-\frac{4}{7}\notin \mathbb{Q}\text{;}$

D. $\frac{3}{5}\in \mathbb{Q}.$

Hướng dẫn giải

Đáp án đúng là: D

Do ‒5 là số nguyên âm, mà ℕ là tập hợp các số tự nhiên nên –5 ∈ ℕ là cách viết sai.

$-\frac{5}{7}$ là số hữu tỉ, mà ℤ là tập hợp các số nguyên nên $-\frac{5}{7}$ là cách viết sai.

$-\frac{4}{7}$ là số hữu tỉ nên $-\frac{4}{7}\notin \mathbb{Q}$ là cách viết sai.

$\frac{3}{5}$ là số hữu tỉ nên cách viết $\frac{3}{5}\in \mathbb{Q}$ là cách viết đúng.

Câu 2. Hình nào biểu diễn số $\frac{1}{3}$và số đối của $\frac{1}{3}$ ?

A.

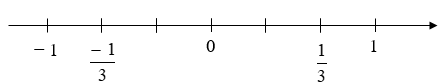
B.

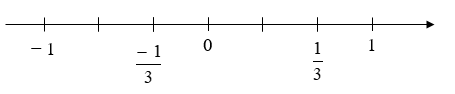
C.

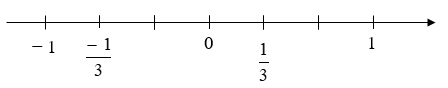
D.

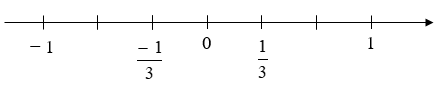
Hướng dẫn giải

Đáp án đúng là: D

Trên trục số, hai số hữu tỉ (phân biệt) có điểm biểu diễn nằm về hai phía của điểm gốc 0 và cách đều điểm gốc 0 được gọi là hai số đối nhau;

Để xác định điểm biểu diễn của số $\frac{1}{3}$, ta chia đoạn từ điểm 0 đến điểm 1 thành 3 phần bằng nhau. Đi theo chiều dương của trục, bắt đầu từ điểm 0, ta lấy 1 phần sẽ được điểm biểu diễn $\frac{1}{3}$ ; lấy điểm đối xứng qua điểm 0 ta được điểm biểu diễn $\frac{-\text{ 1}}{3}.$

Vậy đáp án D biểu diễn số $\frac{1}{3}$và số đối của $\frac{1}{3}$ hay số $\frac{-\text{ 1}}{3}.$

Câu 3. Hãy sắp xếp các số hữu tỉ sau đây theo thứ tự tăng dần $\frac{1}{5},\frac{-\text{ 2}}{5},\frac{3}{7},\frac{-\text{ 1}}{3},0.$

A. $\frac{-\text{ 2}}{5}\text{; }\frac{-\text{ 1}}{3}\text{; 0; }\frac{1}{5}\text{; }\frac{3}{7};$   

B. $\frac{-\text{ 2}}{5}\text{; }\frac{-\text{ 1}}{3}\text{; 0; }\frac{3}{7}\text{; }\frac{1}{5};$

C. $\frac{-\text{ 1}}{3}\text{; }\frac{-\text{ 2}}{5}\text{; 0; }\frac{1}{5}\text{; }\frac{3}{7};$

D. $\frac{-\text{ 1}}{3}\text{; }\frac{-\text{ 2}}{5}\text{; 0; }\frac{3}{7}\text{; }\frac{1}{5}.$

Hướng dẫn giải

Đáp án đúng là: A

Ta có $\frac{-\text{ 1}}{3}\text{ = }\frac{-\text{ 5}}{15}\text{, }\frac{-\text{ 2}}{5}\text{ = }\frac{-\text{ 6}}{15}\text{; }$

Do 0 >  $\frac{-\text{ 5}}{15}\text{ > }\frac{-\text{ 6}}{15}\text{ nên 0 > }\frac{-\text{ 1}}{3}\text{ > }\frac{-\text{ 2}}{5}.$

Lại có: $\frac{3}{7}\text{ = }\frac{15}{35},\frac{1}{5}\text{ = }\frac{7}{35};$

Do $\frac{15}{35}\text{ > }\frac{7}{35}\text{ > 0 nên }\frac{3}{7}\text{ > }\frac{1}{5}>0.$

Suy ra: $\frac{3}{7}\text{ > }\frac{1}{5}\text{ > 0 > }\frac{-\text{ 1}}{3}\text{ > }\frac{-\text{ 2}}{5}.$

Do đó $\frac{-\text{ 2}}{5}\text{ < }\frac{-\text{ 1}}{3}\text{ < 0 < }\frac{1}{5}\text{ < }\frac{3}{7}.$

Vậy sắp xếp các số đã cho theo thứ tự tăng dần là: $\frac{-\text{ 2}}{5}\text{; }\frac{-\text{ 1}}{3}\text{; 0; }\frac{1}{5}\text{; }\frac{3}{7}$ .

Xem thêm Lý thuyết các bài Toán 7 Cánh Diều hay, chi tiết khác:

Lý thuyết Bài 2. Cộng, trừ, nhân, chia số hữu tỉ

Lý thuyết Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ

Lý thuyết Bài 4. Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc

Lý thuyết Bài 5: Biểu diễn thập phân của một số hữu tỉ