Với giải SGK Toán 11 Kết nối tri thức trang 7 chi tiết trong Bài 18: Lũy thừa với số mũ thực giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải Toán 11 trang 7 Tập 2 (Kết nối tri thức)
Luyện tập 3 trang 7 Toán 11 Tập 2: Tính:
Lời giải:
a) .
b) .
HĐ4 trang 7 Toán 11 Tập 2: Nhận biết lũy thừa với số mũ hữu tỉ
a) Với n là số nguyên dương, hãy thử định nghĩa sao cho .
b) Từ kết quả của câu a, hãy thử định nghĩa , với m là số nguyên và n là số nguyên dương, sao cho .
Lời giải:
a) Ta có , mà nên . Do đó, .
b) Ta có .
Theo câu a, ta có nên .
Lời giải:
Ta có a > 0 thì am > 0 với mọi số nguyên m. Khi đó luôn tồn tại căn bậc n của am với n là một số nguyên dương. Do đó, luôn xác định. Vậy trong định nghĩa lũy thừa với số mũ hữu tỉ ta cần điều kiện cơ số a > 0.
Luyện tập 4 trang 7 Toán 11 Tập 2: Rút gọn biểu thức:
Lời giải:
Với x, y > 0, ta có .
3. Lũy thừa với số mũ thực
HĐ5 trang 7 Toán 11 Tập 2: Nhận biết lũy thừa với số mũ thực
Ta biết rằng > là một số vô tỉ và = 1,4142135624...
Gọi (rn) là dãy số hữu tỉ dùng để xấp xỉ số , với r1 = 1; r2 = 1,4; r3 = 1,41;
a) Dùng máy tính cầm tay, hãy tính: và .
b) Có nhận xét gì về sai số tuyệt đối giữa và , tức là 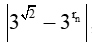
Lời giải:
a) Sử dụng máy tính cầm tay, ta tính được:
;
;
;
;
.
b) Ta có:
Vậy sai số tuyệt đối giữa và là giảm dần khi n càng lớn.
Xem thêm Lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.