Toptailieu.vn xin giới thiệu Lý thuyết Hàm số mũ và hàm số lôgarit (Kết nối tri thức) hay, chi tiết | Lý thuyết Toán 11 Bài viết gồm phần lý thuyết trọng tâm nhất được trình bày một cách dễ hiểu, dễ nhớ bên cạnh đó là bộ câu hỏi trắc nghiệm có hướng dẫn giải chi tiết để học sinh có thể vận dụng ngay lý thuyết, nắm bài một cách hiệu quả nhất. Mời các bạn đón xem:
Lý thuyết Hàm số mũ và hàm số lôgarit (Kết nối tri thức) hay, chi tiết | Lý thuyết Toán 11
A. Lý thuyết Hàm số mũ và hàm số lôgarit
1. Hàm số mũ
a) Khái niệm hàm số mũ
Cho a là số thực dương khác 1.
Hàm số được gọi là hàm số mũ cơ số a.
b) Đồ thị và tính chất của hàm số mũ
Hàm số mũ :
- Có tập xác định là và tập giá trị là ;
- Đồng biến trên khi a > 1 và nghịch biến trên khi 0 < a < 1;
- Liên tục trên ;
- Có đồ thị đi qua các điểm (0; 1), (1; a) và luôn nằm phía trên trục hoành.
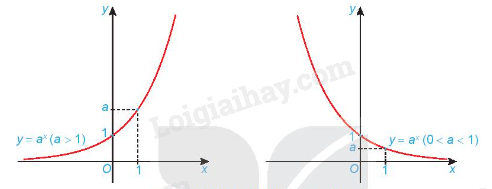
Dạng đồ thị của hàm số
2. Hàm số lôgarit
a) Khái niệm hàm số lôgarit
Cho a là số thực dương khác 1.
Hàm số được gọi là hàm số lôgarit cơ số a.
b) Đồ thị và tính chất của hàm số lôgarit
Hàm số lôgarit :
- Có tập xác định là và tập giá trị là ;
- Đồng biến trên khi a > 1 và nghịch biến trên khi 0 < a < 1;
- Có đồ thị đi qua các điểm (1; 0), (a; 1) và luôn nằm bên phải trục tung.
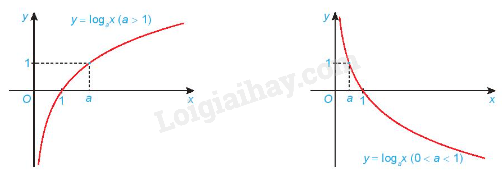
Dạng đồ thị của hàm số
Sơ đồ tư duy Hàm số mũ và hàm số lôgarit
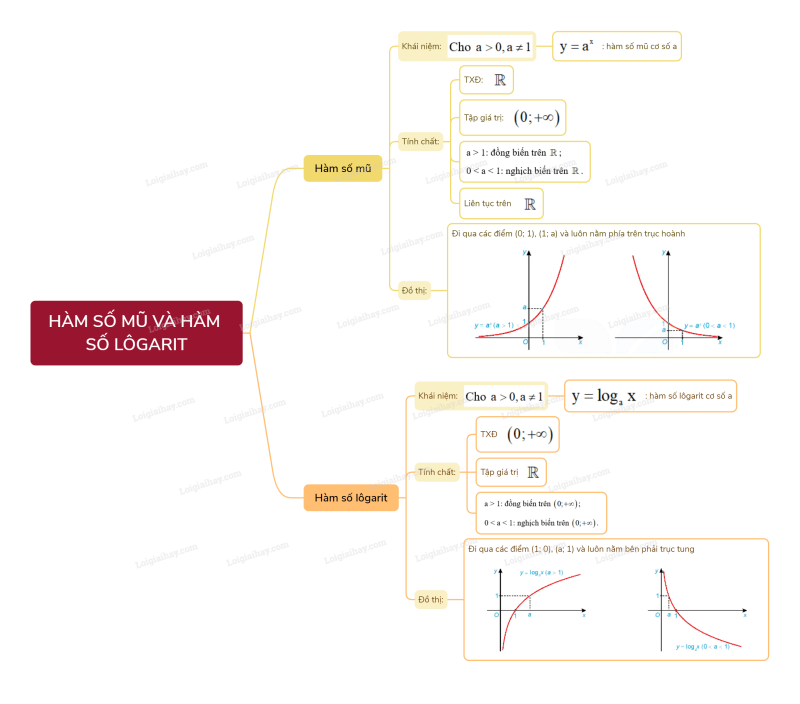
B. Bài tập Hàm số mũ và hàm số lôgarit
Đang cập nhật ...
Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 sách Kết nối tri thức hay, chi tiết khác:
Lý thuyết Bài 21: Phương trình, bất phương trình mũ và lôgarit
Lý thuyết Bài 22: Hai đường thẳng vuông góc
Lý thuyết Bài 23: Đường thẳng vuông góc với mặt phẳng
Lý thuyết Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.