Cho hàm số f(x) = 4sin^2(2x - pi/3). Chứng minh rằng |f'(x)| ≤ 8 với mọi x ℝ. Tìm x để f'(x) = 8

Cho hàm số f(x) = 4sin^2(2x - pi/3). Chứng minh rằng |f'(x)| ≤ 8 với mọi x ℝ. Tìm x để f'(x) = 8

Ngọc Nguyễn Ngày: 21-01-2024 Lớp 11

226

Với Giải Bài 9.13 trang 60 SBT Toán 11 Tập 2 trong Bài 32: Các quy tắc tính đạo hàm Sách bài tập Toán lớp 11 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán lớp 11.

Cho hàm số f(x) = 4sin^2(2x - pi/3). Chứng minh rằng |f'(x)| ≤ 8 với mọi x ℝ. Tìm x để f'(x) = 8

Bài 9.13 trang 60 SBT Toán 11 Tập 2: Cho hàm số f(x) = 4sin² $(2 x - \frac{π}{3})$ . Chứng minh rằng |f'(x)| ≤ 8 với mọi x $\in$ ℝ. Tìm x để f'(x) = 8.

Lời giải:

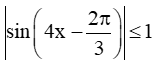
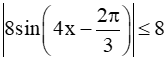
+ Có Cho hàm số f(x) = 4sin^2(2x-pi/3). Chứng minh rằng |f'(x)| nhỏ hơn hoặc bằng 8

Cho hàm số f(x) = 4sin^2(2x-pi/3). Chứng minh rằng |f'(x)| nhỏ hơn hoặc bằng 8

Vì Cho hàm số f(x) = 4sin^2(2x-pi/3). Chứng minh rằng |f'(x)| nhỏ hơn hoặc bằng 8 với mọi x $\in$ ℝ nên với mọi x $\in$ ℝ .

Vậy |f'(x)| ≤ 8 với mọi x $\in$ ℝ.

+ Có f'(x) = 8 $\Leftrightarrow$ 8sin $(4 x - \frac{2 π}{3})$ =8

$\Leftrightarrow \sin (4 x - \frac{2 π}{3}) = 1$

$\Leftrightarrow 4 x - \frac{2 π}{3} = \frac{π}{2} + k 2 π$ (k $\in$ ℤ)

$\Leftrightarrow 4 x = \frac{7 π}{6} + k 2 π$ (k $\in$ ℤ)

$\Leftrightarrow x = \frac{7 π}{24} + k \frac{π}{2}$ (k $\in$ ℤ).

Vậy f'(x) = 8 khi $x = \frac{7 π}{24} + k \frac{π}{2}$ với k $\in$ ℤ.

Xem thêm các bài SBT Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 9.8 trang 60 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:

a) y = (x + 1)²(x² – 1);

b) $y = {(x^{2} - \frac{2}{\sqrt{x}})}^{3}$ .

Bài 9.9 trang 60 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:

a) $y = \frac{x^{2} - x + 1}{x + 2}$ ;

b) $y = \frac{1 - x^{2}}{x^{2} + 1}$ .

Bài 9.11 trang 60 SBT Toán 11 Tập 2: Tính đạo hàm của hàm số $y = 3 \tan (x + \frac{π}{4}) - 2 \cot (\frac{π}{4} - x)$ .

Bài 9.12 trang 60 SBT Toán 11 Tập 2: Cho hàm số $f (x) = c o s^{2} x + c o s^{2} (\frac{2 π}{3} + x) + c o s^{2} (\frac{2 π}{3} - x)$ . Tính đạo hàm f'(x) và chứng tỏ f'(x) = 0 với mọi x $\in$ ℝ.

Bài 9.13 trang 60 SBT Toán 11 Tập 2: Cho hàm số f(x) = 4sin². Chứng minh rằng |f'(x)| ≤ 8 với mọi x ℝ. Tìm x để f'(x) = 8.

Bài 9.14 trang 60 SBT Toán 11 Tập 2: Biết y là hàm số của x thỏa mãn phương trình xy = 1 + lny. Tính y'(0).

Bài 9.15 trang 60 SBT Toán 11 Tập 2: Một vật được phóng thẳng đứng lên trên từ mặt đất với vận tốc ban đầu là v₀ (m/s) (bỏ qua sức cản của không khí) thì độ cao h của vật (tính bằng mét) sau t giây được cho bởi công thức (g là gia tốc trọng trường). Tính vận tốc khi vật chạm đất.

Bài 9.16 trang 60 SBT Toán 11 Tập 2: Chuyển động của một hạt trên một dây rung được cho bởi công thức $s (t) = 10 + \sqrt{2} \sin (4 π t + \frac{π}{6})$ , trong đó s tính bằng centimét và t tính bằng giây. Tính vận tốc của hạt sau t giây. Vận tốc cực đại của hạt là bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất).

Lời giải:

Từ khóa :

Giải bài tập Toán 11

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

224

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

261

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

282

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

233

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.