SBT Toán 8 (Cánh diều) Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)

Mai Hương Ngày: 26-01-2024 Lớp 8

214

Toptailieu.vn biên soạn và giới thiệu lời giải SBT Toán 8 (Cánh diều) Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0) hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi vở bài tập Toán 8 Bài 4 từ đó học tốt môn Toán 8.

SBT Toán 8 (Cánh diều) Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)

Bài 21 trang 61 SBT Toán 8 Tập 1: Trong các phát biểu sau, phát biểu nào đúng?

a) Để vẽ đồ thị của hàm số $y = a x + b (a \neq 0, b \neq 0)$ , ta có thể xác định hai điểm $P (0; b)$ và $Q (- \frac{b}{a}; 0)$ rồi vẽ đường thẳng đi qua hai điểm đó.

b) Để vẽ đồ thị của hàm số $y = a x + b (a \neq 0, b \neq 0)$ , ta có thể xác định hai điểm $M (- 1; - a + b)$ và $N (- \frac{b}{a}; b)$ rồi vẽ đường thẳng đi qua hai điểm đó.

c) Để vẽ đồ thị của hàm số $y = a x + b (a \neq 0, b \neq 0)$ , ta có thể xác định hai điểm $I (1; a + b)$ và $K (- 2; - 2 a + b)$ rồi vẽ đường thẳng đi qua hai điểm đó.

Lời giải:

Phát biểu a và c là phát biểu đúng.

Bài 22 trang 62 SBT Toán 8 Tập 1: Cho các đường thẳng $d_{1} : y = 11 x + 1; d_{2} : y = \sqrt{3} x - 7; d_{3} : y = 2 x - \sqrt{2}$ . Gọi $α_{1}, α_{2}, α_{3}$ lần lượt là các góc tạo bởi đường thẳng $d_{1}, d_{2}, d_{3}$ và trục $O x$ . Sắp xếp các góc $α_{1}, α_{2}, α_{3}$ theo thứ tự số đo tăng dần.

Lời giải:

Gọi hệ số góc của các đường thẳng $d_{1}, d_{2}, d_{3}$ lần lượt là $a_{1}, a_{2}, a_{3}$ . Khi đó, ta có $a_{1} = 11, a_{2} = \sqrt{3}, a_{3} = 2$ . Mà $\sqrt{3} < 2 < 11$ suy ra $a_{2} < a_{3} < a_{1}$ .

Vậy các góc được sắp xếp theo thứ tự tăng dần là: $α_{2}, α_{3}, α_{1}$ .

Bài 23 trang 62 SBT Toán 8 Tập 1: Cho hai đường thẳng $d : y = m x - (2 m + 2)$ và $d^{'} : y = (3 - 2 m) x + 1$ với $m \neq 0$ và $m \neq - \frac{3}{2}$

a) Tìm giá trị của $m$ để đường thẳng $d$ đi qua điểm $A (1; 1)$

b) Gọi $β$ là góc tạo bởi đường thẳng $d$ ở câu a và trục $O x$ . Hỏi $β$ là góc nhọn hay góc tù? Tại sao?

c) Tìm giá trị của $m$ để $d$ cắt $d^{'}$ .

Lời giải:

a) Do đường thẳng $d$ đi qua điểm $A (1; 1)$ nên ta có: $1 = m .1 - (2 m + 2)$ . Suy ra, $m = - 3$ . Vậy với $m = - 3$ thì đường thẳng $d$ đi qua điểm $A (1; 1)$

b) Với $m = - 3$ , ta có đường thẳng $d : y = - 3 x + 4$ . Suy ra hệ số góc của đường thẳng $d$ là $- 3 < 0$ . Vậy góc $β$ là góc tù.

c) Để $d$ và $d^{'}$ cắt nhau thì $m \neq 3 - 2 m$ . Suy ra $m \neq 1$ . Vậy với $m \neq 0, m \neq \frac{3}{2}, m \neq 1$ thì $d$ và $d^{'}$ cắt nhau.

Bài 24 trang 62 SBT Toán 8 Tập 1: Vẽ đồ thị của các hàm số $y = - x, y = - x - 1, y = - \frac{1}{3} x, y = \frac{1}{3} x + 2$ trên cùng một mặt phẳng tọa độ.

Lời giải:

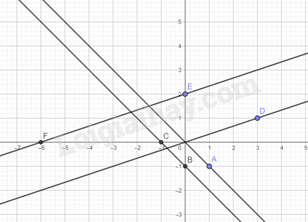
Xét hàm số $y = - x$ . Với $x = 1$ thì $y = - 1$ , ta được điểm $A (1; - 1)$ thuộc đồ thị của hàm số $y = - x$ . Vậy đồ thị của hàm số $y = - x$ là đường thẳng đi qua hai điểm $O (0; 0)$ và $A (1; - 1)$ .

Xét hàm số $y = - x - 1$ . Với $x = 0$ thì $y = - 1$ , ta được điểm $B (0; - 1)$ thuộc đồ thị của hàm số $y = - x - 1$ . Với $y = 0$ thì $x = - 1$ , ta được điểm $C (- 1; 0)$ thuộc đồ thị của hàm số $y = - x - 1$ . Vậy đồ thị của hàm số $y = - x - 1$ là đường thẳng đi qua hai điểm $B (0; - 1)$ và $C (- 1; 0)$ .

Tương tự ta có:

Đồ thị của hàm số $y = \frac{1}{3} x$ là đường thẳng đi qua hai điểm $O (0; 0)$ và $D (3; 1)$ .

Đồ thị của hàm số $y = \frac{1}{3} x + 2$ là đường thẳng đi qua hai điểm $E (0; 2)$ và $F (- 6; 0)$ .

Ta vẽ các đồ thị trên:

Sách bài tập Toán 8 Bài 4 (Cánh diều): Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0) (ảnh 1)

Bài 25 trang 62 SBT Toán 8 Tập 1: Xác định đường thẳng $y = a x + b (a \neq 0)$ đi qua điểm $A (2; 0)$ và song song với đường thẳng $y = 2 x - 5$ . Sau đó vẽ đường thẳng tìm được trên mặt phẳng tọa độ.

Lời giải:

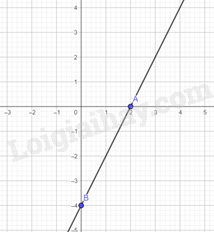
Do đường thẳng $y = a x + b$ song song với đường thẳng $y = 2 x - 5$ nên $a = 2$ (thỏa mãn) và $b \neq - 5$ . Mà đường thẳng $y = a x + b$ đi qua điểm $A (2; 0)$ , suy ra $0 = 2.2 + b$ hay $b = - 4$ (thỏa mãn). Do đó, đường thẳng cần tìm là $y = 2 x - 4$ .

Với $x = 0$ thì $y = - 4$ , ta được điểm $B (0; - 4)$ thuộc đồ thị của hàm số $y = 2 x - 4$ . Vậy đồ thị của hàm số $y = 2 x - 4$ là đường thẳng đi qua hai điểm $A (2; 0)$ và $B (0; - 4)$ .

Sách bài tập Toán 8 Bài 4 (Cánh diều): Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0) (ảnh 2)

Bài 26 trang 62 SBT Toán 8 Tập 1: Một thiết bị tiệt khuẩn y tế bằng năng lượng mặt trời được mua với giá 60 triệu đồng, mỗi năm thiết bị tiệt khuẩn đó đều khấu hao $k$ (triệu đồng) với $0 < k < 60$ . Gọi $y$ (triệu đồng) là giá của thiết bị tiệt khuẩn đó sau $x$ năm sử dụng.

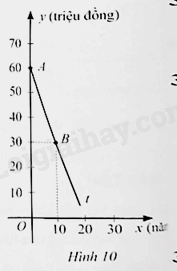
a) Chứng tỏ rẳng $y$ là hàm số bậc nhất của $x$ , tức là $y = a x + b (a \neq 0)$ .

b) Trong Hình 10, tia $A t$ là một phần của đường thẳng $y = a x + b$ . Tìm $a, b$ . Từ đó, cho biết sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng bao nhiêu phần trăm so với giá mua ban đầu.

Sách bài tập Toán 8 Bài 4 (Cánh diều): Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0) (ảnh 3)

Lời giải:

a) Công thức biểu thị giá của thiết bị tiệt khuẩn đó sau $x$ năm sử dụng là: $y = 60 - k x$ hay $y = - k x + 60$ . Mà $k \neq 0$ , suy ra $y$ là hàm số bậc nhất của $x$ .

b) Từ câu a, ta có $b = 60$ . Do đường thẳng $y = a x + b$ đi qua điểm $B (10; 30)$ nên $30 = a .10 + 60$ . Suy ra $a = - 3$ . Khi đó, đường thẳng cần tìm là: $y = - 3 x + 60$ .

Giá của thiết bị tiệt khuẩn đó sau 12 năm sử dụng là:

$- 3.12 + 60 = 24$ (triệu đồng)

Tỉ số phần trăm giữa giá của thiết bị tiệt khuẩn đó sau 12 năm sử dụng và giá mua ban đầu là: $\frac{24.100}{60} % = 40 %$ .

Vậy sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng $40 %$ so với giá mua ban đầu.

Bài 27 trang 62 SBT Toán 8 Tập 1: Cho đường thẳng $d : y = (m - 2) x + 2$ với $m \neq 2$ .

a) Tìm giá trị của $m$ để đường thẳng $d$ cùng với các trục $O x, O y$ tạo thành tam giác có diện tích bằng 2.

b) Chứng tỏ rằng khi giá trị của $m$ thay đổi thì tập hợp các đường thẳng $d$ luôn đi qua một điểm cố định.

Lời giải:

a) Với $y = 0$ thì $x = \frac{- 2}{m - 2}$ , ta được điểm $A (\frac{- 2}{m - 2}; 0)$ là giao điểm của đường thẳng $d$ với trục $O x$ . Khi đó $O A = | \frac{- 2}{m - 2} |$ .

Với $x = 0$ thì $y = 2$ , ta được điểm $B (0; 2)$ là giao điểm của đường thẳng $d$ với trục $O y$ . Khi đó $O B = 2$ .

Ta có diện tích của tam giác $O A B$ bằng 2 nên $\frac{1}{2} . O A . O B = 2$ hay $O A . O B = 4$ .

Suy ra $| \frac{- 2}{m - 2} | .2 = 4$ hay $| \frac{- 2}{m - 2} | = 2$ . Do đó $\frac{- 2}{m - 2} = 2$ hoặc $\frac{- 2}{m - 2} = - 2$ .

Vậy $m = 1$ hoặc $m = 3$ (thỏa mãn) thì đường thẳng $d$ cùng với các trục $O x, O y$ tạo thành tam giác có diện tích bằng 2.

b) Từ câu a, ta có đường thẳng $d$ luôn đi qua điểm $B (0; 2)$ với mọi giá trị của $m$ . Vậy khi giá trị của $m$ thay đổi thì tập hợp các đường thẳng $d$ luôn đi qua điểm $B (0; 2)$ cố định.