Toptailieu.vn biên soạn và giới thiệu lời giải SBT Toán 8 (Cánh diều) Bài tập cuối chương 3 hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi vở bài tập Toán 8 Bài tập cuối chương 3 từ đó học tốt môn Toán 8.
Nội dung bài viết
SBT Toán 8 (Cánh diều) Bài tập cuối chương 3
Bài 28 trang 63 SBT Toán 8 Tập 1: Tọa độ giao điểm của hai đường thẳng d1:y=1−3x4d1:y=1−3x4 và d2:y=−(x3+1)d2:y=−(x3+1) là:
A. (0;−1)(0;−1)
B. (−73;2)(−73;2)
C. (0;14)(0;14)
D. (3;−2)(3;−2)
Lời giải:
Ta có: d1:y=1−3x4=−34x+14d1:y=1−3x4=−34x+14
d2:y=−(x3+1)=−13x−1d2:y=−(x3+1)=−13x−1
Xét đồ thị hàm số d1:y=−34x+14d1:y=−34x+14
Chọn x=0x=0 suy ra y=14y=14
Chọn y=0y=0 suy ra x=13x=13
Vậy đồ thị hàm số d1:y=−34x+14d1:y=−34x+14 là đường thẳng đi qua hai điểm A(0;14),B(13;0)A(0;14),B(13;0)
Xét đồ thị hàm số d2:y=−13x−1d2:y=−13x−1
Chọn x=0x=0 suy ra y=−1y=−1
Chọn y=0y=0 suy ra x=−3x=−3
Vậy đồ thị hàm số d2:y=−13x−1d2:y=−13x−1 là đường thẳng đi qua hai điểm C(0;−1),D(−3;0)C(0;−1),D(−3;0)
Vẽ trên mặt phẳng tọa độ OxyOxy:
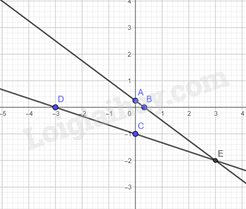
Ta xác định được giao điểm E(3;−2)E(3;−2).
→ Đáp án D.
Lời giải:
Đồ thị của hàm số y=ax+by=ax+b song song với đường thẳng y=2x+1y=2x+1 nên a=2a=2 và b≠1b≠1.
Đồ thị của hàm số y=2x+by=2x+b đi qua điểm M(1;4)M(1;4) nên 4=2.1+b4=2.1+b suy ra b=2b=2
Vậy a.b=2.2=4a.b=2.2=4
→ Đáp án B.
b) Gọi M,NM,N lần lượt là trung điểm của OA,OBOA,OB. Xác định tọa độ các điểm M,NM,N.
c) Tính tỉ số phần trăm của diện tích tam giác OMNOMN và diện tích tam giác OABOAB.
Lời giải:
a) Tọa độ điểm A(−2;0)A(−2;0)
Tọa độ điểm B(0;4)B(0;4)
b) Ta vẽ các điểm M,NM,N:
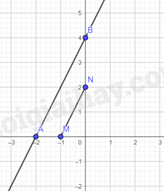
Vậy tọa độ điểm M(−1;0),N(0;2)M(−1;0),N(0;2).
c) Diện tích của tam giác OABOAB bằng: 12.OA.OB12.OA.OB
Mà OM=12OA,ON=12OBOM=12OA,ON=12OB nên ta có diện tích của tam giác OMNOMN bằng:
12.12OA.12OB=14.12.OA.OB12.12OA.12OB=14.12.OA.OB
Vậy tỉ số phần trăm của diện tích tam giác OMNOMN và diện tích tam giác OABOAB là:
14.100%=25%14.100%=25%
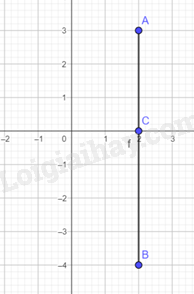
Lời giải:
Ta có: CA+CB≥ABCA+CB≥AB nên CA+CBCA+CB đạt giá trị nhỏ nhất bằng AB=7AB=7. Khi đó, CC là giao điểm của ABAB và trục OxOx. Vậy C(2;0)C(2;0).
a) Đường thẳng dd song song với đường thẳng d1:y=12mx−2d1:y=12mx−2 với m≠0m≠0;
b) Đường thẳng dd trùng với đường thẳng d2:y=x−23m+2d2:y=x−23m+2;
c) Đường thẳng dd và đường thẳng d3:y=√2x−m+2d3:y=√2x−m+2 cắt nhau tại một điểm nằm trên trục OyOy.
Lời giải:
a) Để dd song song với d1d1 thì m−12=12mm−12=12m và 2m−2≠−22m−2≠−2. Suy ra m=1m=1.
Dễ thấy với m=1m=1 ta có dd và d1d1 trở thành d:y=12xd:y=12x và d1:y=12x−2d1:y=12x−2. Khi đó, dd song song với d1d1.
b) Để dd trùng với d1d1 thì m−12=1m−12=1 và 2m−2=−23m+22m−2=−23m+2. Suy ra m=32m=32.
c) Đường thẳng ddvà đường thẳng d3d3 lần lượt cắt trục OyOy tại A(;2m−2)A(;2m−2) và B(0;−m+2)B(0;−m+2). Do đó, dd và d3d3 cắt nhau tại một điểm nằm trên trục OyOy khi m−12≠√2m−12≠√2 và 2m−2=−m+22m−2=−m+2. Suy ra m=43m=43.
Dễ thấy với m=43m=43 ta có dd và d3d3 trở thành d:y=56x+23d:y=56x+23 và d3:y=√2x+23d3:y=√2x+23
Khi đó dd và d3d3 cắt nhau tại điểm (0;23)(0;23) nằm trên trục OyOy
a) Đường thẳng d song song với đường thẳng d′:y=−3x−23 và đi qua điểm A(−2;−4).
Lời giải:
a) Để đường thẳng d song song với đường thẳng d′:y=−3x−23 thì a=a′ vậy đồ thị hàm số của đường thẳng d:y=−3x+b.
Mà d đi qua điểm A(−2;−4), ta có: −4=−3.−2+b suy ra b=−10.
Vậy đường thẳng d:y=−3x−10.
b) B là giao điểm của đường thẳng y=2x−2 với trục hoành nên B(1;0). Từ đó, ta tìm được d:y=−3x+3.
Bài 34 trang 64 SBT Toán 8 Tập 1: Cho hai hàm số y=x+5;y=−x+1.
a) Vẽ đồ thị của hai hàm số đó trên cùng một mặt phẳng tọa độ.
Lời giải:
Xét đồ thị hàm số y=x+5, ta có:
Chọn x=0 suy ra y=5
Chọn y=0 suy ra x=−5
Vậy đồ thị của hàm số y=x+5 là đường thẳng đi qua hai điểm A(0;5),B(−5;0).
Xét đồ thị hàm số y=−x+1, ta có:
Chọn x=0 suy ra y=1
Chọn y=0 suy ra x=1.
Vậy đồ thị của hàm số y=−x+1 là đường thẳng đi qua hai điểm C(0;1), D(1;0)
Vẽ đồ thị hàm số trên mặt phẳng tọa độ:
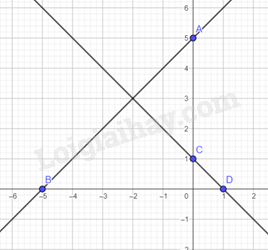
a) Gọi H là hình chiếu của E trên trục Ox
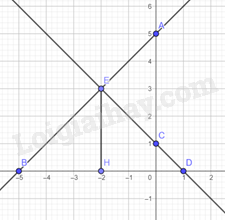
Ta có: E(−2;3),B(−5;0),C(1;0),H(−2;0). Khi đó EH=3cm, BD=6cm
Vậy diện tích của tam giác EBD là: 12.3.6=9(cm2).
a) Viết công thức tính y theo x. Hỏi y có phải là hàm số bậc nhất của x hay không?
Lời giải:
a) y=15x+500. Vậy y là hàm số bậc nhất của x.
b) Mà 140 tháng = 11 năm + 8 tháng, suy ra sau 11 năm 8 tháng kể từ hiện tại thì cô Hạnh có thể mua được căn hộ chung cư đó bằng tiền tiết kiệm.
a) Tính hàm số bậc nhất sao cho đồ thị của hàm số là đường thẳng AB.
Lời giải:
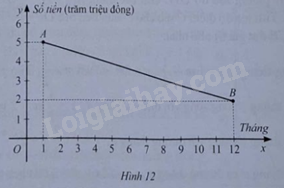
a) Gọi hàm số bậc nhất có đồ thị của hàm số là đường thẳng AB có dạng: y=ax+b với a≠0.
Do đường thẳng AB đi qua điểm A(1;5) và B(12;2) nên ta có: 5=a.1+b và 2=a.12+b hay a+b=5 và 11a+(a+b)=2. Suy ra, a=−311 và b=5811
Vậy hàm số bậc nhất có đồ thị của hàm số là đường thẳng AB là: y=−311x+5811
b) Hợp tác xã đó đã thu được khoảng 18 tấn rau trong tháng 11/2021
Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.