Với giải Bài 24 trang 97 SBT Toán 8 Tập 1 Cánh diều chi tiết trong Bài 5: Hình chữ nhật giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Cho tam giác ABC cân tại A có các đường trung tuyến BM, CN cắt nhau tại G
Bài 24 trang 97 SBT Toán 8 Tập 1: Cho tam giác cân tại có các đường trung tuyến cắt nhau tại . Trên tia đối của tia lần lượt lấy các điểm sao cho . Tứ giác là hình gì? Vì sao?
Lời giải:
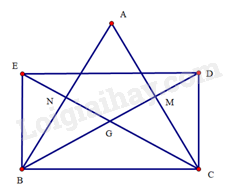
Tứ giác có hai đường chéo và cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
Ta có: nên .
(c.g.c). Suy ra .
Do là trọng tâm của tam giác nên
và
Do đó . Mà là trung điểm của và , suy ra
Hình bình hành có nên là hình chữ nhật.
Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:
Bài 21 trang 97 SBT Toán 8 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
Bài 22 trang 97 SBT Toán 8 Tập 1: Hình 20 mô tả mặt phẳng cắt ngang tầng trệt của một ngôi nhà.
Bài 24 trang 97 SBT Toán 8 Tập 1: Cho tam giác cân tại có các đường trung tuyến cắt nhau tại .
Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.