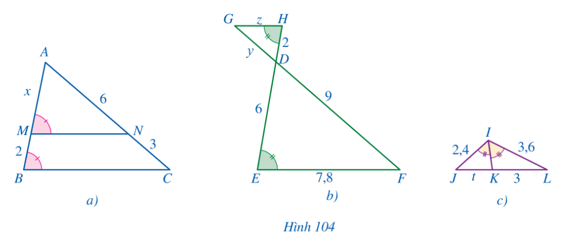
Lời giải:

+ Xét hình 104a:

Theo hình vẽ ta có: $\widehat{\mathrm{AMN}}=\widehat{\mathrm{ABC}}$ mà hai góc ở vị trí đồng vị suy ra MN // BC.

Xét ∆ABC với MN // BC, ta có $\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AN}}{\mathrm{NC}}$ (định lí Thalès)

Hay $\frac{x}{2}=\frac{6}{3}$ nên $x=\frac{2\cdot 6}{3}=4.$

Vậy x = 4.

+ Xét hình 104b:

Theo hình vẽ ta có: $\widehat{\mathrm{GHD}}=\widehat{\mathrm{DEF}}$ mà hai góc ở vị trí so le trong nên GH // EF.

Xét ∆DEF với GH // EF, ta có $\frac{\mathrm{GH}}{\mathrm{EF}}=\frac{\mathrm{GD}}{\mathrm{DF}}=\frac{\mathrm{HD}}{\mathrm{DE}}$ (hệ quả của định lí Thalès)

Hay $\frac{z}{7,8}=\frac{y}{9}=\frac{2}{6}$

Suy ra $z=\frac{7,8\cdot 2}{6}=2,6$ và $y=\frac{9\cdot 2}{6}=3.$

Vậy y = 3 và z = 2,6.

+ Xét hình 104c:

Theo hình vẽ ta có: $\widehat{\mathrm{JIK}}=\widehat{\mathrm{LIK}}$ nên IK là đường phân giác của góc JIL.

Xét ∆IJL có IK là đường phân giác của góc JIL nên $\frac{\mathrm{KJ}}{\mathrm{KL}}=\frac{\mathrm{IJ}}{\mathrm{IL}}$ (tính chất đường phân giác)

Hay $\frac{t}{3}=\frac{2,4}{3,6},$ suy ra $t=\frac{3\cdot 2,4}{3,6}=2.$

Vậy t = 2.

Bài 8 trang 95 Toán 8 Tập 2: Cho Hình 105. Chứng minh:

a) ∆HAB ᔕ ∆HBC;

b) HB = HD = 6 cm.

Lời giải:

a) Xét ∆HAB và ∆HBC có:

$\widehat{\mathrm{AHB}}=\widehat{\mathrm{BHC}}=90°;$ $\widehat{\mathrm{HAB}}=\widehat{\mathrm{HBC}}$ (cùng phụ với góc $\widehat{\mathrm{ABH}})$

Suy ra ∆HAB ᔕ ∆HBC (g.g)

b) Do ∆HAB ᔕ ∆HBC (câu a) nên $\frac{\mathrm{HA}}{\mathrm{HB}}=\frac{\mathrm{HB}}{\mathrm{HC}}$ (tỉ số đồng dạng)

Suy ra HB² = HA.HC = 4 . 9 = 36

Do đó HB = 6 cm.

Xét ∆HAD và ∆HDC có

$\widehat{\mathrm{AHD}}=\widehat{\mathrm{DHC}}=90°;$ $\widehat{\mathrm{HAD}}=\widehat{\mathrm{HDC}}$ (cùng phụ với góc $\widehat{\mathrm{ADH}})$

Do đó ∆HAD ᔕ ∆HDC (g.g)

Suy ra $\frac{\mathrm{HA}}{\mathrm{HD}}=\frac{\mathrm{HD}}{\mathrm{HC}}$ (tỉ số đồng dạng)

Nên HD² = HA.HC = 4 . 9 = 36

Do đó HD = 6 (cm).

Vậy HB = HD = 6 cm.

Bài 9 trang 95 Toán 8 Tập 2: Cho Hình 106. Chứng minh:

a) AH² = AB.AI = AC.AK;

b) $\widehat{\mathrm{AIK}}=\widehat{\mathrm{ACH}}.$

Lời giải:

a) Xét ∆AHI và ∆ABH có:

$\widehat{\mathrm{AIH}}=\widehat{\mathrm{AHB}}=90°;$ $\widehat{\mathrm{BAH}}$ là góc chung

Suy ra ∆AHI ᔕ ∆ABH (g.g)

Do đó $\frac{\mathrm{AH}}{\mathrm{AB}}=\frac{\mathrm{AI}}{\mathrm{AH}}$ (tỉ số đồng dạng)

Nên AH² = AB.AI (1)

Xét ∆AHK và ∆ACH có:

$\widehat{\mathrm{AKH}}=\widehat{\mathrm{AHC}}=90°;$ $\widehat{\mathrm{HAC}}$ là góc chung

Suy ra ∆AHK ᔕ ∆ACH (g.g)

Do đó $\frac{\mathrm{AH}}{\mathrm{AC}}=\frac{\mathrm{AK}}{\mathrm{AH}}$ (tỉ số đồng dạng)

Nên AH² = AC.AK (2)

Từ (1) và (2), suy ra AH² = AB.AI = AC.AK.

b) Ta có: AB.AI = AC.AK (câu a) suy ra $\frac{\mathrm{AK}}{\mathrm{AB}}=\frac{\mathrm{AI}}{\mathrm{AC}}$

Xét ∆AIK và ∆ACB có:

$\widehat{\mathrm{BAC}}$ là góc chung; $\frac{\mathrm{AK}}{\mathrm{AB}}=\frac{\mathrm{AI}}{\mathrm{AC}}$ .

Suy ra ∆AIK ᔕ ∆ACB (c.g.c)

Do đó $\widehat{\mathrm{AIK}}=\widehat{\mathrm{ACB}}$ (hai góc tương ứng).

Vậy $\widehat{\mathrm{AIK}}=\widehat{\mathrm{ACH}}.$

Giải Toán 8 trang 96 Tập 2

Bài 10 trang 96 Toán 8 Tập 2: Cho tam giác ABC có M, N là hai điểm lần lượt thuộc các cạnh AB, AC sao cho MN // BC. Gọi I, P, Q lần lượt là giao điểm của BN và CM, AI và MN, AI và BC. Chứng minh:

a) $\frac{\mathrm{MP}}{\mathrm{BQ}}=\frac{\mathrm{PN}}{\mathrm{QC}}=\frac{\mathrm{AP}}{\mathrm{AQ}};$

b) $\frac{\mathrm{MP}}{\mathrm{QC}}=\frac{\mathrm{PN}}{\mathrm{BQ}}=\frac{\mathrm{IP}}{\mathrm{IQ}}.$

Lời giải:

a) Vì MN // BC, P ∈ MN nên ta có: MP // BQ, PN // QC.

Xét ∆ABQ với MP // BQ, ta có: $\frac{\mathrm{MP}}{\mathrm{BQ}}=\frac{\mathrm{AP}}{\mathrm{AQ}}$ (hệ quả của định lí Thalès)

Xét ∆AQC với PN // QC, ta có: $\frac{\mathrm{PN}}{\mathrm{QC}}=\frac{\mathrm{AP}}{\mathrm{AQ}}$ (hệ quả của định lí Thalès)

Suy ra $\frac{\mathrm{MP}}{\mathrm{BQ}}=\frac{\mathrm{PN}}{\mathrm{QC}}=\frac{\mathrm{AP}}{\mathrm{AQ}}.$

b) Vì MN // BC nên ta có: MP // QC, PN // BQ.

Xét ∆CQI với MP // QC, ta có: $\frac{\mathrm{MP}}{\mathrm{QC}}=\frac{\mathrm{IP}}{\mathrm{IQ}}$ (hệ quả của định lí Thalès)

Xét ∆BQI với PN // BQ, ta có: $\frac{\mathrm{PN}}{\mathrm{BQ}}=\frac{\mathrm{IP}}{\mathrm{IQ}}$ (hệ quả của định lí Thalès)

Suy ra $\frac{\mathrm{MP}}{\mathrm{QC}}=\frac{\mathrm{PN}}{\mathrm{BQ}}=\frac{\mathrm{IP}}{\mathrm{IQ}}.$

Bài 11 trang 96 Toán 8 Tập 2: Cho Hình 107. Chứng minh:

a) ∆ABN ᔕ ∆AIP và AI.AN = AP.AB;

b) AI.AN + BI.BM = AB².

Lời giải:

a) Xét ∆ABN và ∆AIP có:

$\widehat{\mathrm{ANB}}=\widehat{\mathrm{API}}=90°;$ $\widehat{\mathrm{IAP}}$ là góc chung

Suy ra ∆ABN ᔕ ∆AIP (g.g)

Do đó $\frac{\mathrm{AB}}{\mathrm{AI}}=\frac{\mathrm{AN}}{\mathrm{AP}}$ (tỉ số đồng dạng)

Nên AI.AN = AP.AB. (1)

b) Xét ∆ABM và ∆IBP có:

$\widehat{\mathrm{AMB}}=\widehat{\mathrm{IPB}}=90°;$ $\widehat{\mathrm{ABM}}$ là góc chung

Suy ra ∆ABM ᔕ ∆IBP (g.g)

Do đó $\frac{\mathrm{AB}}{\mathrm{IB}}=\frac{\mathrm{BM}}{\mathrm{BP}}$ (tỉ số đồng dạng)

Nên AB.BP = BI.BM (2)

Từ (1) và (2) suy ra

AI.AN + BI.BM = AB.AP + AB.BP

= AB.(AP + BP) = AB.AB = AB².

Vậy AI.AN + BI.BM = AB².

Bài 12 trang 96 Toán 8 Tập 2: Hình 108 minh họa mặt cắt đứng của tủ sách nghệ thuật ở nhà bác Ngọc. Sau một thời gian sử dụng, tủ sách đó đã có dấu hiệu bị xuống cấp và cần sửa lại. Các tấm ngăn BM, CN, DP bị hỏng và cần thay mới. Em hãy giúp bác Ngọc tính toán chiều dài các tấm ngăn mới lần lượt thay thế cho các tấm ngăn BM, CN, DP đã bị hỏng. Biết chiều dài tấm ngăn EQ bằng 4 m.

Lời giải:

Ta có: AB = BC = CD = DE (giả thiết);

AC = AB + BC; CE = CD + DE

Suy ra AC = CE hay C là trung điểm của AE.

Lại có: AM = MN = NP = PQ (giả thiết);

AN = AM + MN; NQ = NP + PQ

Suy ra AN = NQ hay N là trung điểm của AQ.

⦁ Xét ∆AEQ có C, N lần lượt là trung điểm của AE, AQ nên CN là đường trung bình của ∆AEQ

Suy ra $\mathrm{CN}=\frac{1}{2}\mathrm{EQ}=\frac{1}{2}\cdot 4=2$ (m).

⦁ Xét ∆ACN có B, M lần lượt là trung điểm của AC, AN (do AB = BC và AM = MN) nên BM là đường trung bình của ∆ACN.

Do đó $\mathrm{BM}=\frac{1}{2}\mathrm{CN}=\frac{1}{2}\cdot 2=1$ (m).

⦁ Ta có: AD = AB + BC + CD = 3AB, nên $\frac{\mathrm{AB}}{\mathrm{AD}}=\frac{1}{3}.$

AP = AM + MN + NP = 3AM, nên $\frac{\mathrm{AM}}{\mathrm{AP}}=\frac{1}{3}.$

Do đó $\frac{\mathrm{AB}}{\mathrm{AD}}=\frac{\mathrm{AM}}{\mathrm{AP}}=\frac{1}{3}.$

Xét ∆ADP có $\frac{\mathrm{AB}}{\mathrm{AD}}=\frac{\mathrm{AM}}{\mathrm{AP}}$ nên BM // DP (định lí Thalès đảo)

Suy ra (hệ quả của định lí Thalès)

Do đó DP = 3BM = 3.1 = 3 (m).

Vậy BM = 1 m, CN = 2 m, DP = 3 m.

Bài 13 trang 96 Toán 8 Tập 2: Cho Hình 109. Hình nào đồng dạng phối cảnh với:

a) Tam giác OAB? b) Tam giác OBC?

c) Tam giác OCD? d) Tứ giác ABCD?

Lời giải:

a) Ta thấy hai đường thẳng AM, BN cùng đi qua điểm O và $\frac{\mathrm{OM}}{\mathrm{OA}}=\frac{\mathrm{ON}}{\mathrm{OB}}$ nên tam giác OMN đồng dạng phối cảnh với tam giác OAB.

Tương tự như vậy, ta cũng có hình đồng dạng phối cảnh với:

b) Tam giác OBC là: tam giác ONP.

c) Tam giác OCD là: tam giác OPQ.

d) Tứ giác ABCD là: Tứ giác MNPQ.

Bài 14 trang 96 Toán 8 Tập 2: Hình 110 có ghi thứ tự của 6 lá mầm, trong đó có nhiều cặp lá mầm gợi nên những cặp hình đồng dạng. Hãy viết 6 cặp lá mầm gợi nên những hình đồng dạng.

Lời giải:

Cặp 1: Lá mầm 1 và 3;

Cặp 2: Lá mầm 3 và 5;

Cặp 3: Lá mầm 1 và 5;

Cặp 4: Lá mầm 2 và 4;

Cặp 5: Lá mầm 4 và 6;

Cặp 6: Lá mầm 2 và 6.

Xem thêm Lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác:

Bài 6: Trường hợp đồng dạng thứ nhất của tam giác

Bài 7: Trường hợp đồng dạng thứ hai của tam giác

Bài 8: Trường hợp đồng dạng thứ ba của tam giác

Bài 9: Hình đồng dạng

Bài 10: Hình đồng dạng trong thực tiễn