Bài 7 trang 95 Toán 8 Tập 2 | Cánh Diều Giải Toán lớp 8
Bài 7 trang 95 Toán 8 Tập 2: Tính các độ dài x, y, z, t ở các hình 104a, 104b, 104c:
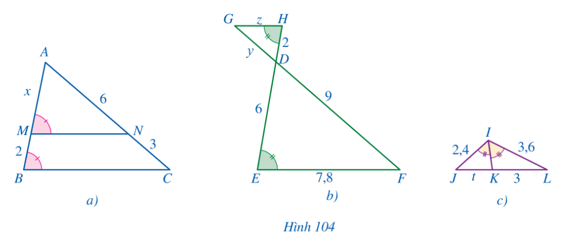
Lời giải:
+ Xét hình 104a:
Theo hình vẽ ta có: mà hai góc ở vị trí đồng vị suy ra MN // BC.
Xét ∆ABC với MN // BC, ta có (định lí Thalès)
Hay nên
Vậy x = 4.
+ Xét hình 104b:
Theo hình vẽ ta có: mà hai góc ở vị trí so le trong nên GH // EF.
Xét ∆DEF với GH // EF, ta có (hệ quả của định lí Thalès)
Hay
Suy ra và
Vậy y = 3 và z = 2,6.
+ Xét hình 104c:
Theo hình vẽ ta có: nên IK là đường phân giác của góc JIL.
Xét ∆IJL có IK là đường phân giác của góc JIL nên (tính chất đường phân giác)
Hay suy ra
Vậy t = 2.
Xem thêm Lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác:
Bài 1 trang 94 Toán 8 Tập 2: Cho ∆DEG ᔕ ∆MNP,
Bài 2 trang 94 Toán 8 Tập 2: Cho ∆DEG ᔕ ∆MNP, DE = 2 cm, DG = 4 cm, MN = 4 cm, NP = 6 cm.
Bài 6 trang 95 Toán 8 Tập 2: Cho ∆ABC ᔕ ∆A’B’C’ với tỉ số đồng dạng k.
Bài 7 trang 95 Toán 8 Tập 2: Tính các độ dài x, y, z, t ở các hình 104a, 104b, 104c:
Bài 8 trang 95 Toán 8 Tập 2: Cho Hình 105. Chứng minh:
Bài 9 trang 95 Toán 8 Tập 2: Cho Hình 106. Chứng minh:
Bài 11 trang 96 Toán 8 Tập 2: Cho Hình 107. Chứng minh:
Bài 13 trang 96 Toán 8 Tập 2: Cho Hình 109. Hình nào đồng dạng phối cảnh với:
Bài 14 trang 96 Toán 8 Tập 2: Hình 110 có ghi thứ tự của 6 lá mầm, trong đó có nhiều cặp lá mầm ....
Xem thêm Lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác:
Bài 6: Trường hợp đồng dạng thứ nhất của tam giác
Bài 7: Trường hợp đồng dạng thứ hai của tam giác
Bài 8: Trường hợp đồng dạng thứ ba của tam giác
Bài 10: Hình đồng dạng trong thực tiễn
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.