Toptailieu.vn xin giới thiệu sơ lược Lý thuyết Sự đồng biến, nghịch biến của hàm số Toán 11 chọn lọc, hay nhất giúp học sinh lớp 11 ôn luyện để nắm chắc kiến thức cơ bản và đạt kết quả cao trong các bài thi môn Toán.
Nội dung bài viết
Mời các bạn đón xem:
Phép đối xứng tâm (Lý thuyết + 35 bài tập có lời giải)
I. Lý thuyết Phép đối xứng tâm
1. Định nghĩa
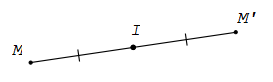
Cho điểm I. Phép biến hình biến điểm I thành chính nó, biến mỗi điểm M khác I thành M’ sao cho I là trung điểm của MM’ được gọi là phép đối xứng tâm I.
Điểm I được gọi là tâm đối xứng.
Phép đối xứng tâm I thường được kí hiệu là ĐI.
Nếu hình H là ảnh của hình H qua ĐI thì ta còn nói H đối xứng với H’ qua tâm I, hay H và H’ đối xứng với nhau qua I.
Từ đinh nghĩa suy ra M = ĐI(M) ⇔ IM'→ = - IM→
2. Biểu thức toạ độ
Với O(0;0), ta có M(x’; y’) = ĐO[M(x;y)] thì
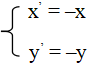
Với I(a; b), ta có M(x’; y’) = ĐI(x’; y’) thì
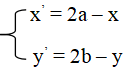
3. Tính chất
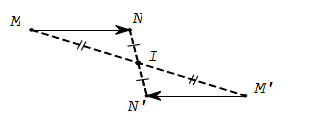
Tính chất 1
Nếu ĐI(M) = M’ và ĐI(N) = N thì M'N'→ = – MN→, từ đó suy ra M’N’ = MN.
Tính chất 2
Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính.
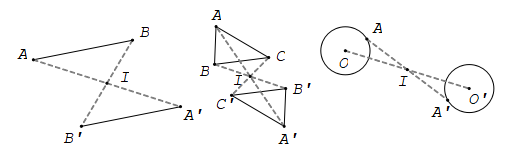
4. Tâm đối xứng của một hình
Định nghĩa
Điểm I được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm I biến hình H thành chính nó.
Khi đó ta nói H là hình có tâm đối xứng.
II. Bài tập Phép đối xứng tâm
Câu 1. Hình nào sau đây có tâm đối xứng?
A. Hình thang.
B. Hình tròn.
C. Parabol.
D. Tam giác bất kì.
Đáp án: B
Câu 2. Cho tam giác ABC có A, B cố định; điểm C di động trên đường thẳng d . Dựng hình bình hành AMBC. Quỹ tích điểm M là:
A. ảnh của đường thẳng d qua phép đối xứng tâm A
B. ảnh của đường thẳng d qua phép đối xứng tâm B
C. ảnh của đường thẳng d qua phép đối xứng tâm I với I là trung điểm AB
D. ảnh của đường thẳng d qua phép đối xứng tâm I với I là trung điểm AC
Đáp án: C
Câu 3. Cho hình bình hành ABCD ( ABCD không là hình thoi). Trên đường chéo BD lấy hai điểm M, N sao cho BM=MN=ND.
Gọi P, Q lần lượt là giao điểm của AN và CD; CM và AB. Tìm mệnh đề sai.
A. P và Q đối xứng qua O
B. M và N đối xứng qua O
C. M là trọng tâm tam giác ABC
D. M là tâm đường tròn ngoại tiếp tam giác ABC
Đáp án: D
Câu 4. Trong các hình sau đây, hình nào không có tâm đối xứng?
A. Hình gồm một đường tròn và một hình chữ nhật nội tiếp.
B. Hình gồm một đường tròn và một tam giác đều nội tiếp.
C. Hình lục giác đều.
D. Hình gồm một hình vuông và đường tròn nội tiếp.
Đáp án: B
Câu 5. Trong các hình dưới đây hình nào không có tâm đối xứng ?
A. Đường elip.
B. Đường hypebol.
C. Đường parabol.
D. Đồ thị hàm số y=sinx.
Đáp án: C
Câu 6. Hình gồm hai đường tròn phân biệt có cùng bán kính có bao nhiêu tâm đối xứng ?
A. 0
B. 1
C. 2
D. Vô số.
Đáp án: B
Câu 7. Cho hai đường thẳng song song d và d' Có bao nhiêu phép đối xứng tâm biến mỗi đường thằng đó thành chính nó?
A. 0
B. 1
C. 2
D. Vô số.
Đáp án: A
Câu 8. Cho hai đường thẳng cắt nhau và Có bao nhiêu phép đối xứng tâm biến mỗi đường thẳng đó thành chính nó?
A. 0
B. 1
C. 2
D. Vô số.
Đáp án: B
Câu 9. Trong mặt phẳng tọa độ cho elip có phương trình Viết phương trình elip là ảnh của elip qua phép đối xứng tâm
A.
B.
C.
D.
Đáp án: B
Câu 10. Cho tam giác không cân. Hai điểm lần lượt là trung điểm của . Gọi O là trung điểm của . Điểm đối xứng với A qua O . Tìm mệnh đề sai.
A. là hình bình hành
B. là hình bình hành
C. đối xứng với nhau qua
D. là hình thoi.
Đáp án: D
Câu 11. Cho bốn đường thẳng trong đó , và cắt . Có bao nhiêu phép đối xứng tâm biến các đường thẳng và lần lượt thành các đường thẳng và ?
A. 0
B. 1
C. 2
D. Vô số.
Đáp án: B
Câu 12. Hình nào sau đây vừa có tâm đối xứng, vừa có trục đối xứng?
A. Hình bình hành.
B. Hình bát giác đều.
C. Hình ngũ giác đều
D. Hình tam giác đều.
Đáp án: B
Câu 13. Hình nào sau đây có trục đối xứng nhưng không có tâm đối xứng?
A. Hình bình hành.
B. Hình bát giác đều.
C. Đường thẳng.
D. Hình tam giác đều.
Đáp án: D
Câu 14. Hình nào sau đây có trục đối xứng và đồng thời có tâm đối xứng?

A. Hình 1 và Hình 2.
B. Hình 1 và Hình 3.
C. Hình 2 và Hình 3.
D. Hình 1, Hình 2 và Hình 3.
Đáp án: C
Câu 15. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Phép đối xứng tâm không có điểm nào biến thành chính nó.
B. Phép đối xứng tâm có đúng một điểm biến thành chính nó.
C. Có phép đối xứng tâm có hai điểm biến thành chính nó.
D. Có phép đối xứng tâm có vô số điểm biến thành chính nó.
Đáp án: B
Câu 16. Mệnh đề nào sau đây là sai?
A. Phép đối xứng tâm bảo toàn khoảng cách giữa hai điểm bất kì.
B. Nếu IM’ = IM thì ĐI(M) = M’.
C. Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với đường thẳng đã cho.
D. Phép đối xứng tâm biến tam giác thành tam giác bằng tam giác đã cho.
Đáp án: BCâu 17. Ảnh của đường thẳng qua phép đối xứng tâm là đường thẳng .
Tính giá trị nhỏ nhất của biểu thức
A.
B.
C.
D.
Đáp án: C
Câu 18. Cho lục giác đều tâm O . Tìm ảnh của tam giác qua phép đối xúng tâm O.
A.
B.
C.
D.
Đáp án: B
Câu 19. Trong mặt phẳng tọa độ cho phép đối xứng tâm biến điểm thành . Mệnh đề nào sau đây là đúng?
A.
B.
C.
D.
Đáp án: B
Câu 20. Trong mặt phẳng tọa độ cho phép đối xứng tâm biến điểm thành điểm có tọa độ là:
A.
B.
C.
D.
Đáp án: BCâu 21. Phép đối xứng tâm biến điểm thành điểm . Tính tổng .
A.
B.
C.
D.
Đáp án: BCâu 22. Phép đối xứng tâm biến điểm thành điểm nằm trên đường thẳng Tìm m .
A.
B.
C.
D.
Đáp án: ACâu 23. Trong mặt phẳng tọa độ cho điểm Thực hiện liên tiếp phép đối xứng qua tâm O và phép tịnh tiến theo vectơ biến điểm M thành điểm nào trong các điểm sau?
A.
B.
C.
D.
Đáp án: DCâu 24. Trong mặt phẳng tọa độ tìm phương trình đường tròn là ảnh của đường tròn : qua phép đối xứng tâm .
A.
B.
C.
D.
Đáp án: DCâu 25. Trong mặt phẳng tọa độ Oxy cho đường thẳng và đường tròn Qua phép đối xứng tâm điểm M trên biến thành điểm N trên Độ dài nhỏ nhất của đoạn MN bằng:
A.
B. 6
C.
D.
Đáp án: DCâu 26. Trong mặt phẳng tọa độ cho đường thẳng Ảnh của đường thẳng d qua phép đối xứng tâm O có phương trình là:
A.
B.
C.
D.
Đáp án: BCâu 27. Trong mặt phẳng tọa độ tìm phương trình đường tròn là ảnh của đường tròn qua phép đối xứng tâm .
A.
B.
C.
D.
Đáp án: ACâu 28. Trong mặt phẳng tọa độ cho đường tròn Giả sử phép đối xứng tâm I biến điểm thành điểm Tìm phương trình của đường tròn là ảnh của đường tròn qua phép đối xứng tâm I.
A.
B.
C.
D.
Đáp án: DCâu 29. Trong mặt phẳng tọa độ cho đường thẳng Ảnh của đường thẳng qua phép đối xứng tâm có phương trình là:
A.
B.
C.
D.
Đáp án: BCâu 30. Trong mặt phẳng tọa độ cho hai đường tròn và có phương trình lần lượt là và .
Xét phép đối xứng tâm I biến và . Tìm tọa độ tâm I .
A.
B.
C.
D.
Đáp án: DCâu 31. Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x - 6y + 5 = 0, điểm I(2;-4). Viết phương trình đường thẳng d' là ảnh của d qua phép đối xứng tâm I.
A. 2x - 6y - 9 = 0.
B. 2x - 6y - 61 = 0.
C. -2x - 6y - 61 = 0.
D. 2x + 6y - 61 = 0.
Đáp án: BCâu 32. Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình x = 2. Trong bốn đường thẳng cho bởi các phương trình sau đường thẳng nào là ảnh của d qua phép đối xứng tâm O?
A. x = -2.
B. y = 2.
C. x = 2.
D. y = -2.
Đáp án: AA. d': x + y - 3 = 0.
B. d': x + 2y - 7 = 0.
C. d': 2x + 2y - 3 = 0.
D. d': x + 2y - 9 = 0.
Câu 34. Trong mặt phẳng Oxy, cho đường thẳng d: Ax + By + C = 0 và điểm I(a;b). Phép đối xứng tâm I biến đường thẳng d thành đường thẳng d' có phương trình:
A. Ax + By + C – 2(Aa + Bb + C) = 0.
B. 2Ax + 2By + 2C – 3(Aa + Bb + C) = 0.
C. Ax + 3By + 2C – 27 = 0.
D. Ax + By + C – Aa – Bb – C = 0.
Đáp án: ACâu 35. Trong mặt phẳng tọa độ Oxy cho phép đối xứng tâm I(1;2) biến điểm M(x;y) thành M'(x';y'). Mệnh đề nào sau đây là đúng?
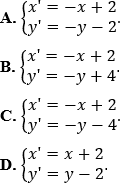
Đáp án: B
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.