Toptailieu.vn xin giới thiệu 30 câu trắc nghiệm Phép đối xứng tâm (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 11 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán. Tài liệu gồm có các nội dung chính sau:

Mời các bạn đón xem:

30 câu trắc nghiệm Phép đối xứng tâm (có đáp án) chọn lọc

Câu 1: Hình có hai đường thẳng a và b song song với nhau thì có bao nhiêu phép đối xứng tâm biến a thành b?

A.  Một      

B.   Hai

C.   Ba      

D.  Vô số

Lời giải:

Đáp án: D

   Chọn đáp án D

   Nhận xét: ba phương án A, B, C đều sai về hướng của vecto

Câu 3: Trong mặt phẳng Oxy cho điểm M(-3;7). Phép đối xứng tâm O biến M thành M’ thì tọa độ M’ là:

A. M’(-3;-7)     

B. M’(3;-7)

C. M’(7;-3)     

D. M’(7;3)

Lời giải:

Đáp án: B

Phép đối xứng tâm O biến M(x;y) thành M’(-x;-y). Chọn đáp án B

Câu 4: Trong mặt phẳng Oxy cho điểm M(2;-6) và điểm I(1;4). Phép đối xứng tâm I biến M

thành M’ thì tọa độ M’ là:

A. M’(0;14)     

B. M’(14;0)   

C. M’(-3/2;-2)     

D. M’(-1/2;5)

Lời giải:

Đáp án: A

   Phép đối xứng tâm I(x₀; y₀) biến M(x; y) thành M'(x'; y') thì:

Thay vào phương trình d ta được :2(4 - x') - 6(-8 - y') + 5 = 0  2x' - 6y' - 61 = 0 hay 2x - 6y - 61 = 0. Chọn đáp án B

Câu 6: Hình nào dưới đây vừa có tâm đối xứng vừa có trục đối xứng?

A. hình bình hành     

B. hình chữ nhật   

C. hình tam giác đều     

D. hình tam giác cân

Lời giải:

Đáp án: B

1. Hình bình hành có tâm đối xứng; hình tam giác cân và hình tam giác đều chỉ có trục đối xứng.

Câu 7: Có bao nhiêu phép đối xứng tâm biến hình chữ nhật thành chính nó?

A. một     

B. hai   

C. ba     

D. không

Lời giải:

Đáp án: A

Câu 8: Trong mặt phẳng Oxy cho điểm M(-5;9). Phép đối xứng tâm I(2; -6) biến M thành M’ thì tọa độ M’ là.

A. M'(9;-15)     

B. M'(9;-3)

C.M'(9;-21)     

D. M'(1;-3)

Lời giải:

Đáp án: C

   Thử vào công thức : Phép đối xứng tâm I(x₀;y₀) biến M(x; y) thành M’(x’, y’) thì

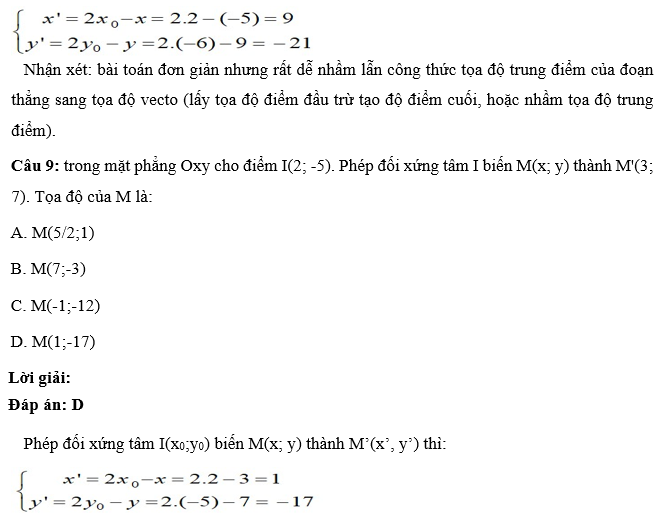
Câu 10: trong mặt phẳng Oxy phép đối xứng tâm I biến M(6; -9) thành M'(3;7). Tọa độ của tâm đối xứng I là:

A. I(-3/2; -8)     

B. (-3;16)

C. (9/2; -1)     

D. I(-3/2; -1)

Lời giải:

Đáp án: C

   Qua phép đối xứng tâm I biến M thành M’ nên I là trung điểm của MM’.

   Tọa độ I bằng trung bình cộng tọa độ của M và M’.

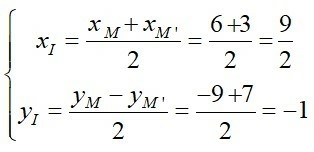
Câu 11: Trong mặt phẳng Oxy cho đường thẳng d có phương trình 6x + 5y - 7 = 0; điểm I(2;-1).

Phép đối xứng tâm I biến d thành d’ có phương trình:

A. 6x - 5y - 7 = 0     

B. 6x + 5y - 7 = 0   

C. 6x - 5y + 7 = 0     

D. 6x + 5y + 7 = 0

Lời giải:

Đáp án: B

   Tâm đối xứng I thuộc d thì phép đối xứng tâm I biến d thành chính nó.

   Nhận xét: lưu ý kiểm tra xem tâm có thuộc d không, cũng như với phép tịnh tiến thì kiểm tra xem vecto tịnh tiến có cùng phương với vecto chỉ phương của d không.

Câu 12: Trong mặt phẳng Oxy cho hình (H) gồm đường thẳng d có phương trình : 3x - 5y + 7 = 0; đường thẳng d’ có phương trình 3x - 5y + 12 = 0. Một lần đối xứng của (H) là:   

A. (1;2)     

B. (-4;0)     

C. (0;19/2)     

D. (19/2;0)

Lời giải: Đáp án: C

   Hai đường thẳng d và d’ song song. Điểm A(1; 2) thuộc d và điểm B(-4; 0) thuộc d’ nên bị loại    Tính khoảng cách từ C tới hai đường thẳng d, d’

Lời giải: Đáp án: C

   Đường thẳng d có vecto chỉ phương u→(5;3); Đường thẳng d’ có vecto chỉ phương v→(-3;1) nên d không song song với d’. Tâm đối xứng của hình (H) chính là giao điểm của d và d’:

   Gọi I là giao điểm của d và d’.

   Điểm I thuộc d’ nên tọa độ I(2- 3t; 4+ t)

   Lại có, I thuộc d nên thay tọa độ điểm I vào phương trình đường thẳng d ta được: 3(2 - 3t) - 5(4 + t) + 7 = 0  -14t = 7

Câu 15: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x² + y² + 2x - 6y + 6 = 0; điểm I(1;2). Phép đối xứng tâm I biến (C) thành (C’) có phương trình:

A.  x² + y² - 6x - 2y + 6 = 0

B.   x² + y² - 2x - 6y + 6 = 0

C.   x² + y² + 6x - 2y - 6 = 0   

D.  D. x² + y² - 6x + 2y + 6 = 0

Lời giải:

Đáp án: A

   Phép đối xứng tâm I(1; 2) biến M(x; y) thành M’(x’; y’) thì:

Lời giải:

Đáp án: A

   Phép đối xứng tâm I biến M(x; y) thành M’(x’; y’) thì:

Câu 20. Hình nào sau đây có tâm đối xứng?

A. Hình thang.

A.   Hình tròn.

B.   Parabol.

C.   Tam giác bất kì.

Lời giải:

Đáp án: B

Giải thích:

Tâm đối xứng của hình tròn là tâm của hình tròn đó

Câu 21. Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x - 6y + 5 = 0, điểm I(2;4). Viết phương trình đường thẳng d' là ảnh của d qua phép đối xứng tâm I.

A. 2x - 6y - 9 = 0.

B.   2x - 6y - 61 = 0.

C.   -2x - 6y - 61 = 0.

D.   2x + 6y - 61 = 0.

Lời giải:

Đáp án: B Giải thích:

Lấy M(x;y) thuộc d, phép đối xứng tâm I(x₀,y₀) biến M(x;y) thành M'(x',y')

Chọn A.

Câu 23. Cho điểm I(1;1) và đường thẳng d: x + 2y + 3 = 0. Tìm ảnh của d qua phép đối xứng tâm I.

A.   d': x + y - 3 = 0.

B.   d': x + 2y - 7 = 0.

C.   d': 2x + 2y - 3 = 0.

D.   d': x + 2y - 9 = 0.

Lời giải:

Đáp án: D

Giải thích:

Cách 1. Gọi d’ là ảnh của d qua phép đối xứng tâm I.

Với mỗi điểm M(x;y) ∈ d qua phép đỗi xứng tâm ta có M'(x';y') ∈ d'

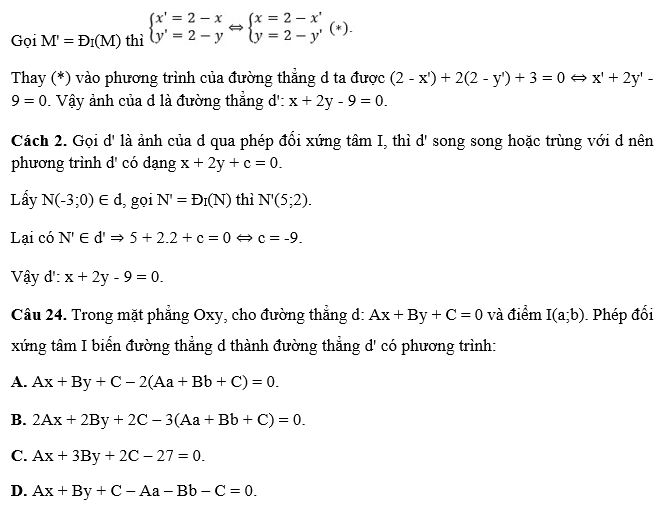
Lời giải:

Đáp án: A

Giải thích:

Biểu thức tọa độ của phép đối xứng tâm là

Ta có d: Ax + By + C = 0 nên A(2a - x') + B(2b - y') + C = 0

Do đó Ax' + By' - (2Aa + 2Bb + C) = 0 hay Ax' + By' + C – 2(Aa + Bb + C) = 0

Câu 25. Trong mặt phẳng tọa độ Oxy cho phép đối xứng tâm I(1;2) biến điểm M(x;y) thành M'(x';y'). Mệnh đề nào sau đây là đúng?

Câu 26. Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng Δ: x + 2y - 3 = 0 và Δ': x - 2y - 7 =

0. Qua phép đối xứng tâm I(1;-3), điểm M trên đường thẳng Δ biến thành điểm N thuộc đường thẳng Δ'. Tính độ dài đoạn thẳng MN.

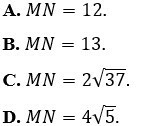
Lời giải:

Đáp án: D Giảithích:

Lấy điểm M(3-2m;m) thuộc Δ.

Gọi N là ảnh của M qua phép đối xứng tâm I(1;-3) → N(2m-1;-6-m).

Vì N ∈ Δ' nên (2m-1)-2(-6-m)-7=0 ⇔ m = -1.

Câu 28. Trong mặt phẳng Oxy, tìm ảnh của đường tròn x² + (y – 2)² = 4. qua phép đối xứng tâm

I(-2;-1):

A.  (x + 4)² + (y + 4)² = 4

B.   (x + 2)² + (y + 1)² = 4

C.  (x - 4)² + (y - 4)² = 4

D. (x + 4)² + (y - 4)² = 4

Lời giải:

Đáp án: A

Giải thích:

Đường tròn có tâm O(0,2), bán kính r = 2

Gọi O' là ảnh của O qua phép đối xứng tâm I khi đó ta có x_O' = 2x_I - x_O = -4; y_O' ⁡ = 2y_I - y_O = -4  O'(-4;-4)

Như vậy ảnh của đường tròn qua phép đối xứng tâm là:

(x + 4)² + (y + 4)² = 4

Câu 29. Trong mặt phẳng Oxy. Phép đối xứng tâm I biến đường tròn (C): (x + 1)² + (y – 2)² =

16 thành đường tròn(C'): (x + 3)² + (y – 10)² = 16 tìm tọa độ tâm I

A. I(-2;6)

B.   I(2;6).

C.   I(-2;-6).

D.   I(6;-2).

Lời giải:

Đáp án: A

Giải thích:

●   (C) có tâm J(-1;2)

●   (C') có tâm J'(-3;10)

Tâm đối xứng I là trung điểm của JJ’ suy ra I(-2;6)

Câu 30. Trong mặt phẳng tọa độ Oxy cho điểm M(2;1). Thực hiện liên tiếp phép đối xứng qua tâm O và phép tịnh tiến theo vectơ  = (1;2) biến điểm M thành điểm nào trong các điểm sau? A. A(1;3).

B.   B(2;0).

C.   C(0;2).

D.   D(-1;1).

Lời giải:

Đáp án: D

Giải thích:

Phép đối xứng tâm O(0;0) biến điểm M(2;1) thành điểm M'(-2;-1).

Phép tịnh tiến theo vectơ  = (1;2) biến điểm M'thành điểm M"