Đường tiệm cận (Lý thuyết + 50 bài tập có lời giải)

A .Tóm tắt lý thuyết

1. Đường tiệm cận ngang

    - Cho hàm số y = f(x) xác định trên một khoảng vô hạn (là khoảng dạng (a; +∝), (-∝; b) hoặc (-∝; +∝). Đường thẳng y = y₀ là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn

    - Nhận xét: Như vậy để tìm tiệm cận ngang của đồ thị hàm số ta chỉ cần tính giới hạn của hàm số đó tại vô cực.

2. Đường tiệm cận đứng

    - Đường thẳng x = x₀ được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn

B. Bài tập 

Bài 1. Cho hàm số y = f(x) có  và  . Khẳng định nào sau đây là khẳng định đúng ?

 

A. Đồ thị hàm số không có tiệm cận ngang.

B. Đồ thị hàm số có đúng một tiệm cận ngang.

C. Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng y = 1 và y = -1.

D. Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng x = 1 và x = -1.

Đáp án: C

Theo định nghĩa về tiệm cận, ta có:

+  nên y = 1 là một tiệm cận ngang.

+  nên y = - 1 là một tiệm cận ngang.

Vậy đồ thị hàm số đã cho có 2 tiệm cận ngang là y = 1 và y= -1.

Bài 2. Cho hàm số y= f(x) có  và  . Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số không có tiệm cận ngang.

B. Đồ thị hàm số nằm phía trên trục hoành.

C. Đồ thị hàm số có một tiệm cận ngang là trục hoành.

D. Đồ thị hàm số có một tiệm cận đứng là đường thẳng y = 0

Đáp án: C

Ta có  nên đường thẳng y =0 là tiệm cận ngang của đồ thị hàm số.

→ Đáp án B sai vì chọn hàm  .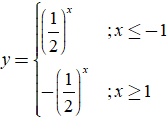

Vậy ta chỉ có đáp án C đúng.

Bài 3. Cho hàm số y= f(x) có  và  . Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số đã cho không có tiệm cận đứng

B. Trục hoành và trục tung là hai tiệm cận của đồ thị hàm số đã cho

C. Đồ thị hàm số đã cho có một tiệm cận đứng là đường thẳng y= 0

D. Hàm số đã cho có tập xác định là  .

Đáp án: B

Theo định nghĩa về tiệm cận, ta có:

+  nên đường thẳng y= 0 là tiệm cận ngang.

+ Và  nên đường thẳng x= 0 là thẳng x= 0 là tiệm cận đứng.

Bài 4. Cho hàm số y= f(x) có  và  . Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số không có tiệm cận ngang.

B. Đồ thị hàm số có hai tiệm cận ngang.

C. Đồ thị hàm số có tiệm cận ngang y= -1 và tiệm cận đứng x = 10 .

D. Đồ thị hàm số hai tiệm cận ngang là các đường y = -1 và y = 10.

Đáp án: C

Theo định nghĩa về tiệm cận, ta có

+  nên đường thẳng y= -1 là tiệm cận ngang của đồ thị hàm số.

+ Lại có:  nên đường thẳng x= 10 là tiệm cận đứng.

Bài 5. Cho hàm số y= f(x) có  và  Khẳng định nào sau đây là đúng?

A. Đồ thị hàm số có một tiệm cận ngang là y=1 và đường thẳng x= 2 không phải là tiệm cận đứng.

B. Đồ thị hàm số có tiệm cận ngang y= 1 và tiệm cận đứng x= 2.

C. Đồ thị hàm số có tiệm cận ngang y= 1 và tiệm cận đứng x= 10.

D. Đồ thị hàm số không có tiệm cận ngang nhưng có một tiệm cận đứng x=2.

Đáp án: A

Theo định nghĩa về tiệm cận, ta có:

+  nên y= 1 là tiệm cận ngang.

+ Lại có:  nên x= 2 không phải là tiệm cận đứng.

Bài 6. Cho hàm số y= f(x) có tập xác định là D=(- 3;3)\{-1; 1}, liên tục trên các khoảng của tập D và có:

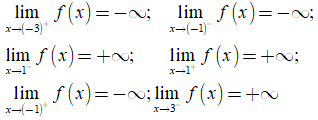
Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số có đúng hai TCĐ là các đường thẳng x = -3 và x = 3.

B. Đồ thị hàm số có đúng hai TCĐ là các đường thẳng x = - 1 và x = 1.

C. Đồ thị hàm số có đúng bốn TCĐ là các đường thẳng x = ±1 và x = ±3 .

D. Đồ thị hàm số có sáu TCĐ.

Đáp án: C

Dựa vào định nghĩ đường tiệm cận ta có các đường thẳng x = ±1 và x = ±3 là các tiệm cận đứng của đồ thị .

Bài 7. Chọn khẳng định đúng trong các khẳng định sau:

A. Đồ thị hàm số y= f(x) có tiệm cận ngang y= 1 khi và chỉ khi  và 

B. Nếu hàm số y= f(x) không xác định tại x0 thì đồ thị hàm số y= f(x) có tiệm cận đứng x= x0.

C. Đồ thị hàm số y=f(x) có tiệm cận đứng x= 2 khi và chỉ khi  và 

D. Đồ thị hàm số y= f(x) bất kì có nhiều nhất hai đường tiệm cận ngang.

Đáp án: D

* A sai vì chỉ cần một trong hai giới hạn  hoặc  tồn tại thì đã suy ra được tiệm cận ngang là y= 1.

* B sai, ví dụ hàm số  không xác định tại x= - 2 nhưng  và  không tiến đến vô cùng nên x= -2 không phải là tiệm cận đứng của đồ thị hàm số.

* C sai vì chỉ cần tồn tại một trong bốn giới hạn sau:

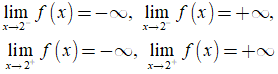
* D đúng vì chỉ có hai giới hạn 

Bài 8. Cho hàm số y= f(x) xác định và liên tục trên R\ {-1}, có bảng biến thiên như sau:

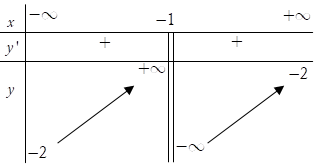
Khẳng định nào sau đây là khẳng định đúng ?

A. Đồ thị hàm số có tiệm cận đứng y= -1 và tiệm cận ngang x= - 2.

B. Đồ thị hàm số có duy nhất một tiệm cận.

C. Đồ thị hàm số có ba tiệm cận.

D. Đồ thị hàm số có tiệm cận đứng x= -1 và tiệm cận ngang y=-2.

Đáp án: D

Từ bảng biến thiên, ta có :

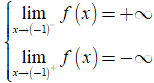*  nên x= -1 là TCĐ.

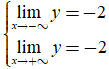*  nên y= -2 là TCN.

Bài 9. Cho hàm số y= f(x) xác định trên R\{0}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

Mệnh đề nào sau đây là đúng?

A. Đồ thị hàm số có một đường tiệm cận đứng.

B. Hàm số đạt cực tiểu tại x = 0.

C. Giá trị lớn nhất của hàm số là 2.

D. Hàm số không có cực trị.

Đáp án: A

Dựa vào bảng biến thiên, ta có nhận xét như sau:

* A đúng vì  nên x= 0là tiệm cận đứng của đồ thị hàm số.

* B sai vì tại x= 0 hàm số không xác định.

* C sai vì hàm số đạt giá trị lớn nhất bằng 1 trên khoảng  mà không đạt giá trị lớn nhất trên khoảng 

* D sai vì đạo hàm y’ đổi dấu từ “+” sang “-“ khi đi qua điểm x= 1 nên x= 1 là điểm cực đại của hàm số.

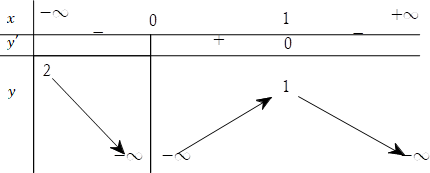
Bài 10. Cho hàm số y = f(x) có bảng biến thiên như sau

Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận?

A. 1     B. 2     C. 3     D. 4

Đáp án: C

Từ bảng biến thiên, ta có:

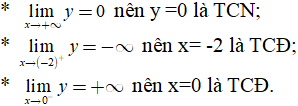
Vậy đồ thị hàm số đã cho có đúng ba đường tiệm cận.

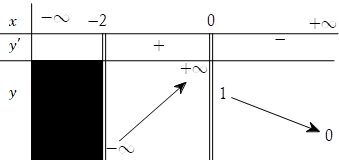
Bài 11. Cho hàm số y = f(x) có bảng biến thiên như sau:

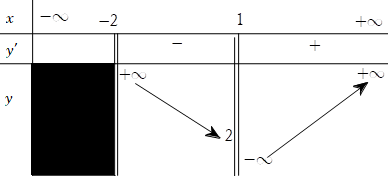
Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận?

A. 1     B. 2     C. 3     D. 4

Đáp án: B

Từ bảng biến thiên, ta có:

*  nên đồ thị hàm số không có tiệm cận ngang;

*  nên x= -2 là TCĐ;

*  nên x=1 là TCĐ.

Vậy đồ thị hàm số đã cho có đúng hai đường tiệm cận.

Bài 12. Tìm tọa độ giao điểm của đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số 

A. ( -2; 2)     B. (2; 1)     C.(-2; -2)     D. (- 2; 1)

Đáp án: D

TXĐ: D= R\{- 2}

Dễ thấy đồ thị hàm số có tiệm cận đứng là x= -2.

Lại có:  nên đồ thị hàm số có tiệm ngang y =1.

Suy ra giao điểm của hai đường tiệm cận là ( -2; 1) .

Bài 13. Tìm số tiệm cận đứng của đồ thị hàm số  .

A. 2.     B. 3.     C. 0.     D. 1.

Đáp án: D

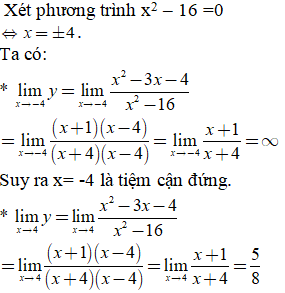
Suy ra; x= 4 không là tiệm cận đứng.

Vậy đồ thị hàm số có duy nhất một tiệm cận đứng.

Bài 14. Đồ thị hàm số  có tất cả bao nhiêu đường tiệm cận?

A. 1.     B. 2.     C. 3.     D. 4.

Đáp án: C

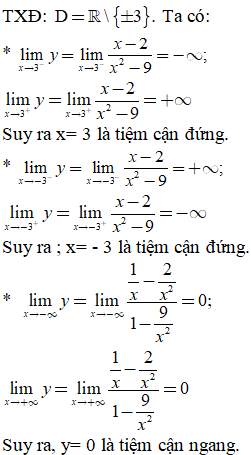
Vậy đồ thị hàm số có đúng ba tiệm cận

Bài 15. Đồ thị hàm số nào trong các hàm số dưới đây có tiệm cận đứng?

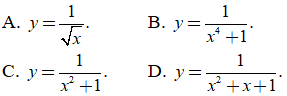
Đáp án: A

* Nhận thấy các đáp án B, C, D hàm số có TXĐ: D= R nên không có tiệm cận đứng.

* Dùng phương pháp loại trừ thì A đúng.

(Thật vậy; hàm số  có  nên x=0 là tiệm cận đứng)

Bài 16. Đồ thị hàm số 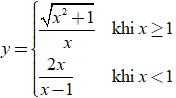 có tất cả bao nhiêu đường tiệm cận?

A. 1.     B. 2.     C. 3.     D. 4.

Đáp án: C

Ta có:

*  nên x= 1 là tiệm cận đứng.

*  nên y= 2 là tiệm cận ngang.

*  nên y= 1 là tiệm cận ngang.

Vậy đồ thị hàm số có đúng ba tiệm cận.

Bài 17. Tìm tất cả các đường tiệm cận của đồ thị hàm số 

A. Đồ thị hàm số f(x) có đúng một tiệm cận ngang là đường thẳng y=3 và không có tiệm cận đứng.

B. Đồ thị hàm số f(x) không có tiệm cận ngang và có đúng một tiệm cận đứng là đường thẳng x= -1.

C. Đồ thị hàm số f(x) có tất cả hai tiệm cận ngang là các đường thẳng y= -3; y=3 và không có tiệm cận đứng.

D. Đồ thị hàm số f(x) không có tiệm cận ngang và có đúng hai tiệm cận đứng là các đường thẳng x= 1; x= -1.

Đáp án: C

* TXĐ: D= R nên đồ thị không có tiệm cận đứng.

*Ta có  nên y= -3 là tiệm cận ngang.

 nên y= 3 là tiệm cận ngang.

Bài 18. Đồ thị hàm số 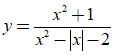 có tất cả bao nhiêu đường tiệm cận

A. 1.     B. 2.     C. 4.     D. 3.

Đáp án: D

Ta có 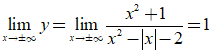 nên y= 1 là tiệm cận ngang.

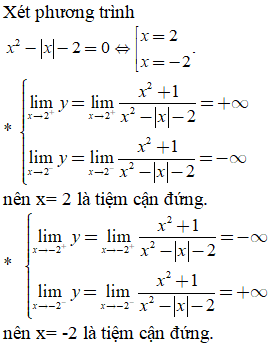
Vậy đồ thị hàm số đã cho có ba đường tiệm cận.

Bài 19. Đồ thị hàm số nào sau đây có đúng hai tiệm cận ngang?

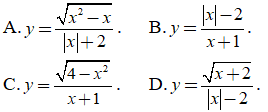
Đáp án: B

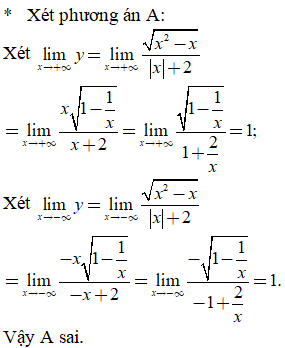
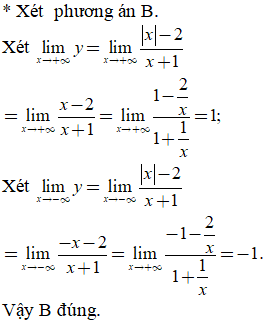
* C và D có thể loại trừ vì TXĐ không chứa 

Bài 20. Cho hàm số 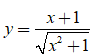 . Mệnh đề nào sau đây là đúng?

A. Đồ thị hàm số có đúng một tiệm cận đứng, không có tiệm cận ngang.

B. Đồ thị hàm số có đúng hai tiệm cận đứng, không có tiệm cận ngang.

C. Đồ thị hàm số có đúng hai tiệm cận ngang, không có tiệm cận đứng.

D. Đồ thị hàm số có đúng một tiệm cận đứng và một tiệm cận ngang.

Đáp án: C

* Do TXĐ: D= R nên đồ thị hàm số không có tiệm cận đứng.

* Ta có:

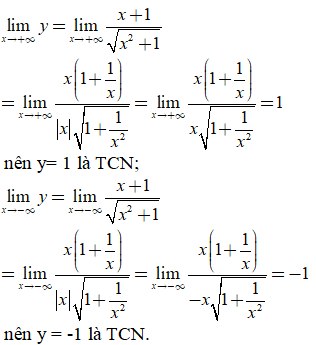
Vậy đồ thị hàm số không có tiệm cận đứng và có đúng hai tiệm cận ngang.

Bài 21. Đồ thị hàm số 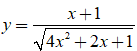 có tất cả bao nhiêu đường tiệm cận?

A. 1     B. 2     C . 3     D. 4

Đáp án: B

* Ta có  nên TXĐ của hàm số là D= R. Do đó đồ thị hàm số không có tiệm cận đứng.

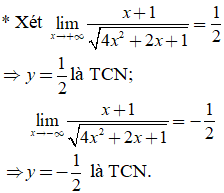
Vậy đồ thị hàm số có đúng hai đường tiệm cận.

Bài 22. Đồ thị hàm số  có tất cả bao nhiêu đường tiệm cận?

A. 1     B. 2     C. 3     D. 0

Đáp án: C

TXĐ:  . Ta có:

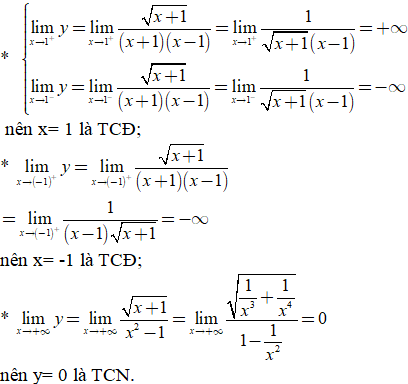
Vậy đồ thị hàm số có đúng ba đường tiệm cận.

Bài 23. Đồ thị hàm số 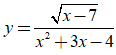 có bao nhiêu đường tiệm cận đứng?

A. 1.     B. 2.     C. 0.     D. 3.

Đáp án: C

Tập xác định: 

Vì  . Do đó đồ thị hàm số không có tiệm cận đứng.

Bài 24. Đồ thị hàm số 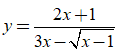 có bao nhiêu đường tiệm cận ngang?

A. 1.     B. 2.     C. 3.     D. 4.

Đáp án: A

Tập xác định: 

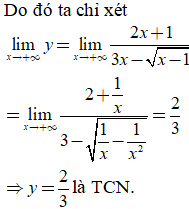
Vậy đồ thị hàm số có đúng một TCN.

Bài 25. Gọi n; d lần lượt là số đường tiệm cận ngang và số đường tiệm cận đứng của đồ thị hàm số 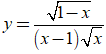 . Khẳng định nào sau đây là đúng?

A. n = d = 1     B. n = 0; d = 1

C. n = 1; d = 2     D. n = 0; d = 2

Đáp án: D

* Tập xác định: D= (0; 1) nên không tồn tại 

Suy ra đồ thị hàm số không có tiệm cận ngang.

* Xét phương trình 

Ta có:

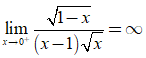+  nên x= 0 là TCĐ.

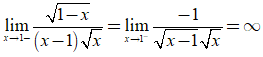+  nên x= 1 là TCĐ.

Vậy n=0; d = 2 .

Bài 26. Đồ thị hàm số 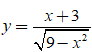 có tất cả bao nhiêu đường tiệm cận?

A. 0      B. 1     C. 2     D. 3

Đáp án: B

+ Tập xác định D= (-3; 3) nên không tồn tại 

Suy ra đồ thị hàm số không có tiệm cận ngang.

Ta có:

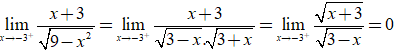*  nên x= - 3 không là TCĐ;

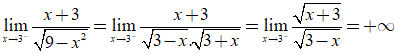*  nên x= 3 là TCĐ.

Vậy đồ thị hàm số đã cho có đúng một tiệm cận.

Bài 27. Đồ thị hàm số 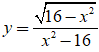 có tất cả bao nhiêu đường tiệm cận?

A. 0     B. 1     C. 2     D. 3.

Đáp án: C

* Tập xác định: D = ( -4; 4) nên không tồn tại 

Suy ra đồ thị hàm số không có tiệm cận ngang.

Ta có:

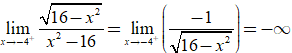*  nên x= - 4 là TCĐ;

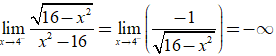*  nên x=4 là TCĐ.

Vậy đồ thị hàm số đã cho có đúng hai tiệm cận.

Bài 28. Đồ thị hàm số 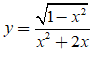 có tất cả bao nhiêu đường tiệm cận?

A. 0     B. 1     C. 2     D. 3.

Đáp án: B

+ Tập xác định:  nên không tồn tại  Suy ra đồ thị hàm số không có tiệm cận ngang.

* Ta có 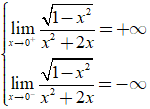 nên x= 0 là TCĐ.

Vậy đồ thị hàm số có đúng một tiệm cận.

Bài 29. Đồ thị hàm số 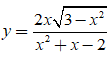 có tất cả bao nhiêu đường tiệm cận?

A. 3.     B. 1.     C. 2.     D. 4.

Đáp án: B

* Tập xác định  nên không tồn tại  Suy ra đồ thị hàm số không có tiệm cận ngang.

* Ta có 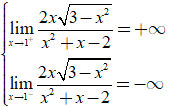 nên x= 1 là TCĐ.

Vậy đồ thị hàm số có đúng một tiệm cận.

Bài 30. Đồ thị hàm số 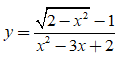 có tất cả bao nhiêu đường tiệm cận?

A. 0.     B. 1.     C. 2.     D. 3.

Đáp án: A

* Tập xác định  nên không tồn tại  Suy ra đồ thị hàm số không có tiệm cận ngang.

* Ta có 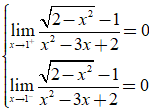 nên đồ thị hàm số không có tiệm cận đứng.

Vậy đồ thị hàm số không có tiệm cận.

Bài 31. Giá trị của m để tiệm cận đứng của đồ thị hàm số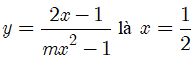 

A. m = 2     B. m = - 2     C. m = 4     D. m ≠ 4

Đáp án: C

Để đường thẳng  là tiệm cận đứng của đồ thị hàm số đã cho khi và chỉ khi:

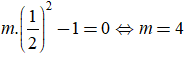
Bài 32. Giá trị của m để tiệm cận ngang của đồ thị hàm số 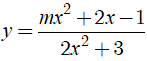 là y = 2

A. m = 2     B. m = -2     C. m = 4     D. m = -4

Đáp án: C

Ta có:

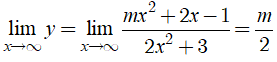
Do đó; để đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số đã cho khi và chỉ khi:

Bài 33. Cho hàm số 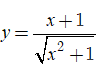 . Phát biểu nào sau đây là đúng?

A. Tiệm cận đứng của đồ thị hàm số là x = 1

B. Tiệm cận đứng của đồ thị hàm số là x = ±1

C. Tiệm cận ngang của đồ thị hàm số là y = 1 và y = - 1.

D. Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là x = ±1, y = 1

Đáp án: C

Ta có;

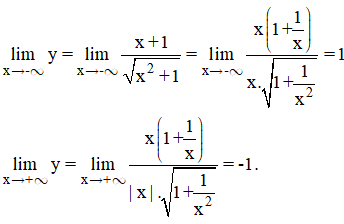
Do đó; đồ thị hàm số đã cho có 2 tiệm cận ngang là y = 1 và y = - 1

Bài 34. Đồ thị hàm số nào sau đây không có tiệm cận ngang:

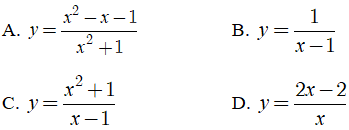
Đáp án: C

* Cách 1: Xét phương án C; ta có:

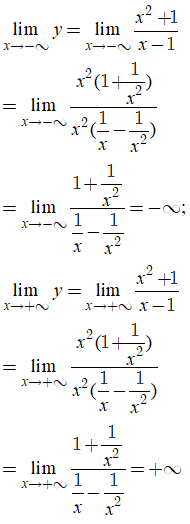
Do đó, đồ thị hàm số này không có tiệm cận ngang.

Cách 2. Cho một hàm số phân thức; nếu bậc cao nhất của tử lớn hơn bậc cao nhất của mẫu thức thì đồ thị hàm số không có tiệm cận ngang.

Bài 35. Số các đường tiệm cận của hàm số  là:

A. 0     B. 1     C. 2     D. 3

Đáp án: D

* Phương trình 3- x2 = 0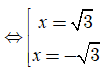 

Do đó, đồ thị hàm số có hai tiệm cận đứng là 

* Lại có: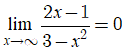 

Do đó,đồ thị hàm số đã cho có 1 đường tiệm cận ngang là y = 0 .

Vậy đồ thị hàm số có tất cả 3 đường tiệm cận.

Bài 36. Với giá trị nào của m thì đồ thị hàm số 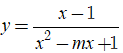 có ba đường tiệm cận

A. m > 2 hoặc m < - 2     B. m > 2 hoặc m < -1

C. m > 1 hoặc m < -1     D. Đáp án khác

Đáp án: A

* Ta có;

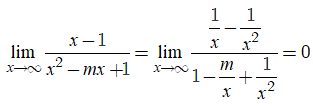
Do đó, đồ thị hàm số đã cho có 1 đường tiệm cận ngang là y = 0.

* Bài toán trở thành tìm m để đồ thị hàm số có hai tiệm cận đứng . Điều này xảy ra khi và chỉ khi

Phương trình: x2 - mx+ 1 = 0 có 2 nghiệm phân biệt khác 1.

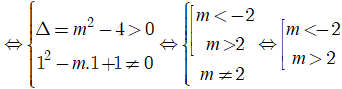
Vậy để đồ thị hàm số có 3 đường tiệm cận khi và chỉ khi m < -2 hoặc m > 2.

Bài 37. Số các đường tiệm cận của hàm số 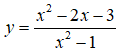 là:

A. 3      B. 2     C. 1     D. 0

Đáp án: B

* Ta có:

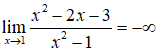
⇒ đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.

Lại có:

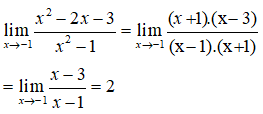
Suy ra; đường thẳng x = - 1 không là tiệm cận đứng của đồ thị hàm số.

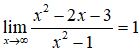
Suy ra; tiệm cận ngang là y = 1.

Vậy đồ thị hàm số đã cho có tất cả 2 đường tiệm cận,

Bài 38. Số các đường tiệm cận của hàm số 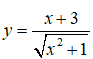 là:

A. 0     B. 1     C. 2     D. 3

Đáp án: C

* Hàm số đã cho luôn xác định với mọi giá trị của x nên đồ thị hàm số đã cho không có tiệm cận đứng.

* Ta có:

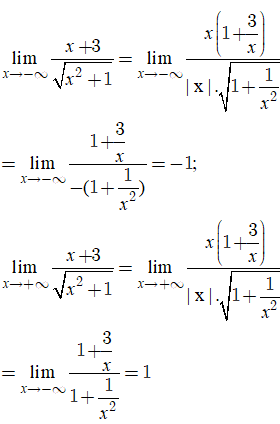
Do đó, đồ thị hàm số đã cho có 2 đường tiệm cận ngang là y = 1 và y = - 1.

Vậy đồ thi hàm số đã cho có tất cả hai đường tiệm cận

Bài 39. Cho hàm số  có tiệm cận đứng là x = 2 và đồ thị hàm số đi qua điểm A(3; -1). Tính m+ n

A. -1     B. - 3     C. - 2     D. 3

Đáp án: B

* Do đồ thị hàm số đã cho có tiệm cận đứng là x = 2 nên ta có:

2+ n = 0 ⇔ n = - 2 .

Khi đó; hàm số đã cho có dạng 

* Lại có; điểm A(3; -1) thuộc đồ thị hàm số nên ta có:

Vậy m+ n = -1+ ( - 2) = - 3

Bài 40. Cho hàm số 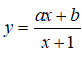 có tiệm cận ngang là y = 4 và đồ thị hàm số đi qua điểm A( -2;0) thì hiệu a- b bằng:

A. 2     B. 4     C. - 2     D. - 4

Đáp án: D

Do đồ thị hàm số có tiệm cận ngang là y = 4 nên ta có:

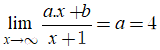
Khi đó; hàm số đã cho có dạng: 

Do đồ thị hàm số đi qua điểm A( - 2; 0) nên ta có:

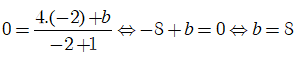
Suy ra; a –b = - 4

Bài 41. Gọi x, y, z lần lượt là số các đường tiệm cận của đồ thị các hàm số sau: 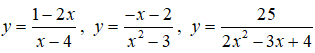 . Bất đẳng thức nào sau đây đúng?

A. x < y < z     B. y < x < z

C. z < x < y     D. z < y < x

Đáp án: C

Ta tìm số đường tiệm cận của từng đồ thị hàm số.

+ Xét hàm số 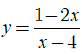 có tiệm cận đứng là x = 4 và tiệm cận ngang y = - 2.

⇒ x = 2.

+ Xét hàm số  có tiệm cận đứng là  và tiệm cận ngang là y = 0 .

Do đó y = 3

+ xét hàm số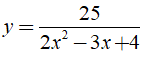 

Không có tiệm cận đứng và có tiệm cận ngang là y = 0 .

Do đó; z = 1.

Vậy z < x < y.

Bài 42. Cho hàm số 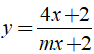 . Với giá trị nào của m thì hàm số có tiệm cận ngang là y = 2?

A . m = 1     B. m = - 1     C. m = 2     D. m = -2

Đáp án: C

Ta có:

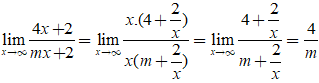
Do đó, để đường thẳng y = 2 là đường tiệm cận ngang của đồ thị hàm số thì:

Bài 43. Cho hàm số 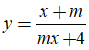 . Với giá trị nào của m thì hàm số có tiệm cận đứng là x = 2?

A. m = 1     B. m = 2

C. m = - 2     D.Không có giá trị thỏa mãn.

Đáp án: D

Điều kiện để hàm số không suy biến là:

Khi đó; để đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số thì :

2m+ 4 = 0 ⇔ m = - 2 ( không thỏa mãn điều kiện).

Vậy không có giá trị nào của m thỏa mãn.

Bài 44. Đồ thị hàm s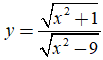ố  có:

A. Có 1 tiệm cận đứng, không có tiệm cận ngang

B. Không có tiệm cận đứng, có tiệm cận ngang

C. Không có tiệm cận đứng, 1 tiệm cận ngang

D. Có 2 tiệm cận đứng, 1tiệm cận ngang

Đáp án: D

* Ta có:

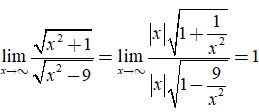
Do đó; đồ thị hàm số đã cho có một tiệm cận ngang là y = 1.

+ Ta có:

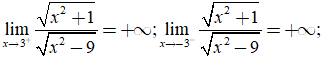 nên đồ thị hàm số đã cho có 2 tiệm cận đứng là x = 3 và x = - 3.

Bài 45. Với giá trị nào của m thì đồ thị  có 2 đường tiệm cận

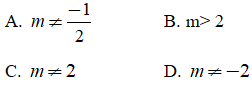
Đáp án: A

Điều kiện để hàm số không suy biến là:

+ Với điều kiện trên; đồ thị hàm số có tiệm cận đứng là x = - 2.

+ Do  nên đồ thị hàm số có tiệm cận ngang là y = m.

Vậy nếu 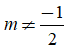 thì đồ thị hàm số đã cho có 2 tiệm cận

Bài 46. Cho hàm số  . Tìm m để đồ thị hàm số nhận điểm I( 1; 1) làm tâm đối xứng.

A. m = 1     B. m ≠ -1     C. m ≠ 1     D. m > 1

Đáp án: B

Điều kiện để hàm số không suy biến là:

Với điều kiện trên; đồ thị hàm số có tiệm cận đứng là x = 1 và tiệm cận ngang là y = 1.

Do đó, tâm đối xứng của đồ thị hàm số là I ( 1; 1) ( là giao điểm của hai đường tiệm cận).

Bài 47. Cho hàm số  . Tìm m để đồ thị hàm số nhận điểm I ( 2; 2) làm tâm đối xứng

A. m = 2     B. m = 3     C. m = -3     D. m = - 2

Đáp án: A

+ Điều kiện để hàm số không bị suy biến là:

+ Với điều kiện trên, đồ thị hàm số có tiệm cận đứng là x = 2 và tiệm cận ngang là y = m.

Khi đó, tâm đối xứng của đồ thị hàm số là A( 2; m) là giao điểm của hai đường tiệm.

+ Do đó, để điểm I (2; 2) khi và chỉ khi m = 2.

Bài 48. Cho hàm số  . Tìm m để đồ thị hàm số nhận điểm I ( 3; 1) làm tâm đối xứng của đồ thị?

A. m = 1

B. m = -2

C. m = - 1

D. Không có giá trị nào thỏa mãn.

Đáp án: D

+ Điều kiện để hàm số không bị suy biến là:

+ Với điều kiện trên; đồ thị hàm số có tiệm cận ngang là  và tiệm cận đứng là 

+ Để điểm I (3;1) làm tâm đối xứng của đồ thị nên ta có:

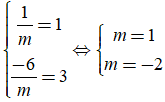
Do đó; không có giá trị nào của m thỏa mãn đầu bài.

Bài 49. Cho hàm số y = f(x) xác định, liên tục trên R\ {3}và có bảng biến thiên như hình dưới đây. Số các phát biểu đúng trong các phát biểu sau là ?.

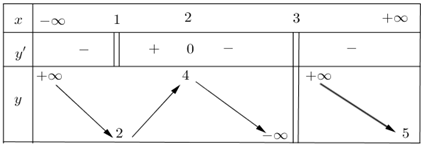
1) Đồ thị hàm số đã cho có đúng một tiệm cận đứng

2) Đồ thị hàm số đã cho có đúng một tiệm cận ngang

3) Đồ thị hàm số đã cho có hai điểm cực trị

4) Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng x = 1 và x = 3

Số các phát biểu sai trong các phát biểu sau là ?.

A. 1     B. 2     C. 3     D. 4

Đáp án: A

Dựa vào bảng biến thiên; đồ thị hàm số có tiệm cận đứng là x = 3 và tiệm cận ngang là y = 5.

Hàm số có hai điểm cực trị là x = 1 và x = 2.

Chú ý: tại x = 1 đạo hàm của hàm số không xác định; đường thẳng x = 1 không là tiệm cận đứng của đồ thị hàm số.

Bài 50. Tìm tiệm cận đứng của đồ thị hàm số: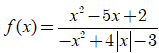 

A. y = - 1     B. x = 1; x = 3

C. y = 1; y = 3.     D. x = ±1; x = ±3.

Đáp án: D

Ta có:

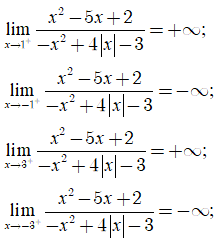
Do đó, đồ thị hàm số đã cho có 4 đường tiệm cận là x = 1; x = -1; x = 3 và x = - 3