Giá trị lớn nhất và giá trị nhỏ nhất của hàm số (Lý thuyết + 50 bài tập có lời giải)
Nội dung bài viết
A. Tóm tắt lý thuyết
Định nghĩa:
Cho hàm số y = f(x) xác định trên miền D
- Số M gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu: 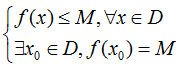 .
.
Kí hiệu: ![]() hoặc
hoặc ![]() .
.
- Số m gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu: 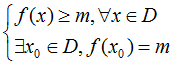 .
.
Kí hiệu: ![]() hoặc
hoặc ![]()
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số liên tục trên K (K có thể là khoảng, đoạn, nửa khoảng, ...)
1. Quy trình tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sử dụng bảng biến thiên
- Bước 1. Tính đạo hàm f'(x).
- Bước 2. Tìm các nghiệm của f'(x) và các điểm f'(x) trên K.
- Bước 3. Lập bảng biến thiên của f(x) trên K.
- Bước 4. Căn cứ vào bảng biến thiên kết luận ![]()
2. Quy trình tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số không sử dụng bảng biến thiên
** Trường hợp 1. Tập K là đoạn [a; b]
- Bước 1. Tính đạo hàm f'(x) .
- Bước 2. Tìm tất cả các nghiệm xi ∈ [a; b] của phương trình f'(x) = 0 và tất cả các điểm α ∈ [a; b] làm cho f'(x) không xác định.
- Bước 3. Tính f(a), f(b), f(xi), f(αi).
- Bước 4. So sánh các giá trị tính được và kết luận ![]() .
.
** Trường hợp 2. Tập K là khoảng (a; b)
- Bước 1. Tính đạo hàm f'(x) .
- Bước 2. Tìm tất cả các nghiệm xi ∈ (a; b) của phương trình f'(x) = 0 và tất cả các điểm αi ∈ (a; b) làm cho f'(x) không xác định.
- Bước 3. Tính ![]() .
.
- Bước 4. So sánh các giá trị tính được và kết luận ![]() .
.
** Chú ý: Nếu giá trị lớn nhất (nhỏ nhất) là A hoặc B thì ta kết luận không có giá trị lớn nhất (nhỏ nhất).
C. Bài tập trắc nghiệm
Câu 1: Giá trị lớn nhất của hàm số f(x)=-x2+4 là:
A. 0
B. 4
C. 2
D. không có đáp án
Tập xác định: D = R. Ta có
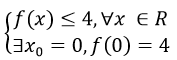
Do đó giá trị lớn nhất của hàm số f(x) là 4 đạt được khi x = 0. Chọn đáp án B.
Câu 2: Giá trị lớn nhất của hàm số
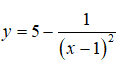
đạt được khi x nhận giá trị bằng:
A. 1 B. 5 C. 0 D. Không có đáp án.
Tập xác định: D = R \ {1}
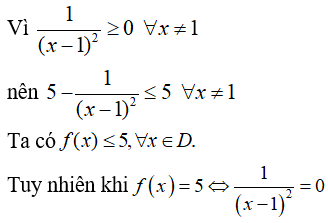
=> không tồn tại x thỏa mãn. Do đó hàm số không có giá trị lớn nhất. Chọn đáp án D
Câu 3: Giá trị lớn nhất của hàm số y = x(5 - 2x)2 trên [0; 3] là:
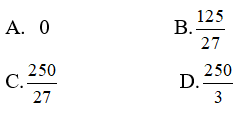
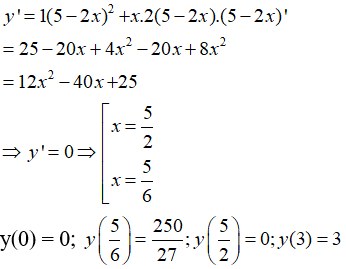
Vậy GTLN của hàm số trên [0; 3] là 250/27 đạt được khi x = 5/6. Chọn đáp án C.
Câu 4: Giá trị lớn nhất của hàm số
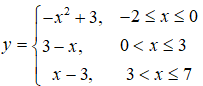
có đồ thị như hình bên là
A. 3 B. 7
B. -1 D. 4
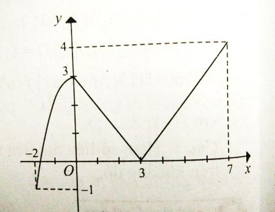
Chọn đáp án D.
Chú ý. Cần phân biệt giá trị lớn nhất của hàm số và cực đại của hàm số.
Câu 5: Một công ti quản lí chuẩn bị xây dựng một khu chung cư mới. Họ tính toán nếu tòa nhà có x căn hộ thì chi phí bảo trì của tòa nhà là: C(x) = 4000 - 14x + 0,04x2. Khu đất của họ có thể xây được tòa nhà chứa tối đa 300 căn hộ. Hỏi họ nên xây dựng tòa nhà có bao nhiêu căn hộ để chi phí bảo trì của tòa nhà là nhỏ nhất?
A. 150 B.175 C. 300 D.225
Ta có x là số căn hộ. Rõ ràng x phải thỏa mãn điều kiện 0 ≤ x ≤ 300. Chi phí bảo trì tòa nhà C(x) = 4000 - 14x + 0,04x2
Ta phải tìm 0 ≤ xo ≤ 300 sao cho C(xo) có giá trị nhỏ nhất.
Ta có C'(x) = -14 + 0,08x, 0 ≤ x ≤ 300. C'(x) = 0 <=> x = 175
Trên đoạn [0; 300] ta có C(0) = 4000; C(175) = 2775; C(300) = 3400
Từ đó ta thấy C(x) đạt giá trị nhỏ nhất khi x = 175. Chọn đáp án B.
Câu 6: GTLN của hàm số y = -x2 + 4x + 7 đạt được khi x bằng:
A. 11 B. 4
C. 7 D. 2
y' = -2x + 4 = 0 <=> x = 2
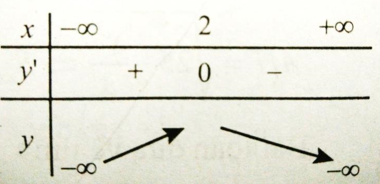
Dựa vào bảng biến thiên; GTLN của hàm số là 11 khi x= 2.
Chọn đáp án D.
Chú ý. Cần phân biệt GTLN của hàm số (max y) với giá trị x để hàm số đạt được GTLN.
Câu 7: GTLN của hàm số
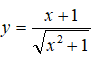
trên khoảng (0; 4) đạt được
A. x = 1 B. x = -1 C. x = √2 D. Không tồn tại
Xét
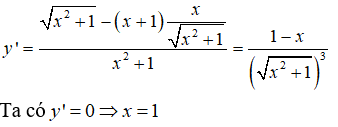
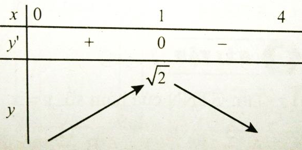
Ta có y' = 0 => x = 1
Vậy hàm số có GTLN bằng √2 khi x = 1 . Chọn đáp án A.
Câu 8: Tìm GTLN của hàm số
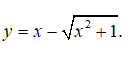
A. 0 B. +∞ C. Không tồn tại D. Không có đáp án
Tập xác định R.
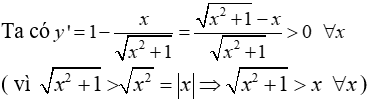
Ta có bảng biến thiên:
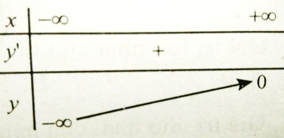
Hàm số không có GTLN trên R . Chọn đáp án C.
Câu 9: Một hành lang giữa hai tòa tháp có hình dạng một hình lăng trụ đứng. Hai mặt bên ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật dài 20m, rộng 5m. Với độ dài xấp xỉ nào của BC thì thể tích hành lang này lớn nhất
A. 6m B. 7m
C. 8m D. 9m.
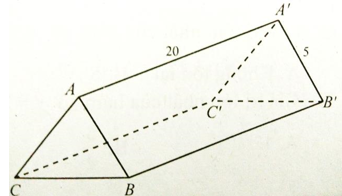
Thể tích hình lăng lớn nhất khi và chỉ khi diện tích ΔABC lớn nhất.
Gọi độ dài BC là x (m). Kẻ AH ⊥ BC.
Bài toán đưa về tìm x ∈ (0; 10) để hàm số y = x√(100-x2) có giá trị lớn nhất.
Ta có:
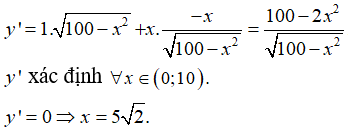
Bảng biến thiên:
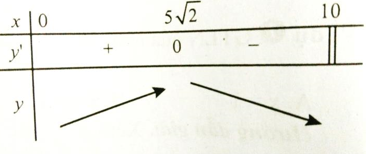
Hàm số đạt giá trị lớn nhất tại x = 5√2 ≈ 7. Chọn đáp án B.
Câu 10: Tìm GTNN của hàm số y = x2 - 3x + 5
A. 3/2 B. 11/4 C. 3 D. 5
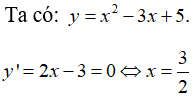
Lập bảng biến thiên ta được, hàm số đạt giá trị nhỏ nhất tại:
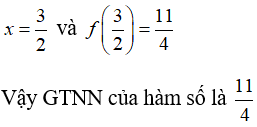
Câu 11: GTLN của hàm số y = sin2x - √3cosx trên đoạn [0; π] là
A. 1 B. 7.4 C. 2 D. 1/4
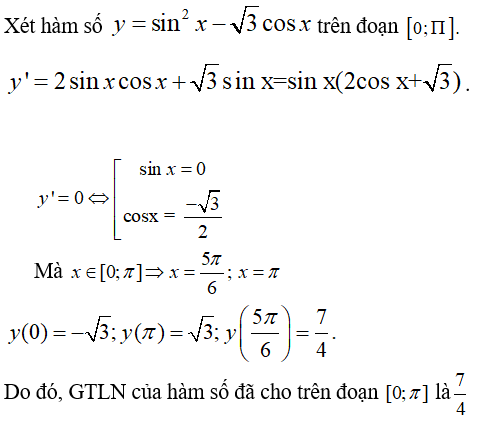
Câu 12: GTNN của hàm số y = x3 + 3x2 - 9x + 1 trên đoạn [-4;4] là
A. -4 B. 1 C. 4 D. -1
Xét hàm số y = x3 + 3x2 - 9x + 1 trên đoạn [-4;4].
Ta có:
y(1) = -4, y(-3) = 28; y(4) = 77; y(-4) = 21
GTNN của hàm số y = X3 - 9x + 1 trên đoạn [-4;4] là -4 khi x= 1
Câu 13: GTLN của hàm số y = x4 - 8x2 + 16 trên đoạn [-1;3] là
A. 0 B. 15 C. 25 D. 30
Xét hàm số y = x4 - 8x2 + 16 trên đoạn [-1;3]
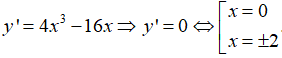
y(0) = 16, y(2) = 0; y(-1) = 9; y(3) = 25
GTLN của hàm số y = x4 - 8x + 16 trên đoạn [-1;3] là 25 khi x = 3.
Câu 14: GTNN của hàm số y = x/(x+2) trên nửa khoảng (-2;4] là
A. 0 B. 1 C.2/3 D. Không tồn tại
Xét hàm số
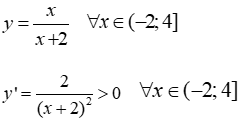
Ta có bảng biến thiên
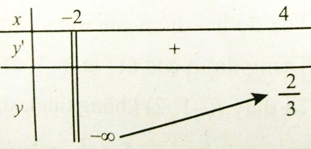
Hàm số không có GTNN
Câu 15: GTNN của hàm số y = x + 2 + 1/(x - 1) trên khoảng (1; +∞) là:
A. Không tồn tại B. 3/2 C. 2 D = 7/4
Xét hàm số

Trên (1; +∞) y' = 0 => x = 2. Bảng biến thiên
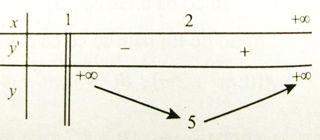
Giá trị nhỏ nhất của hàm số là y=5.
Câu 16: GTLN của hàm số y = 2sinx + cos2x trên đoạn [0; π] là
A. 1 B. 3/2 C. 2 D. 7/4
Xét hàm số y=2sin x + cos 2x trên đoạn
y’=2cos x- 2sin 2x = 2cos x(1- 2sin x)
Trên đoạn [0; π]
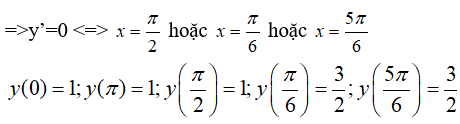
Giá trị lớn nhất của hàm số này trên [0; π] là y = 3/2 .
Câu 17: Cho hàm số y = f(x) xác định và liên tục trên R và có bảng biến thiên. Khẳng định nào sau đây là khẳng định đúng?
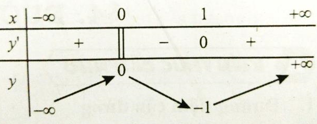
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 1.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1.
D. Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 1Dựa vào định nghĩa, hàm số không tồn tại giá trị lớn nhất và giá trị nhỏ nhất. Hàm số đạt cực đại tại x=0 và cực tiểu tại x=1.
Câu 18: Xét hàm số
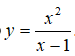
Trong các khẳng định sau, khẳng định nào là đúng?
A. Hàm số có giá trị lớn nhất bằng 4.
B. Hàm số có giá trị cực đại bằng 4
C. Hàm số có giá trị lớn nhất bằng 0.
D. Hàm số có giá trị cực đại bằng 0
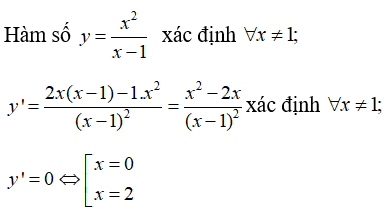
Bảng biến thiên
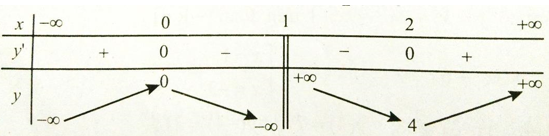
Hàm số không tồn tại giá trị lớn nhất. Hàm số có giá trị cực đại bằng 0.
Câu 19: Cho tấm nhôm hình vuông cạnh 12cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại như hình vẽ bên để được một cái hộp không nắp. Với giá trị nào của x thì hộp nhận được có thể tích lớn nhất?
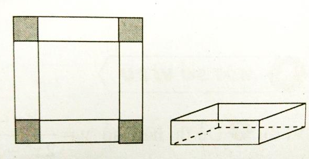
A. 6 B. 4 C.3 D.2
Hình hộp có đáy là hình vuông cạnh: 12 - 2x
Chiều cao của hình hộp là: x
Thể tích hình hộp là y = x(12 - 2x)2
Bài toán đưa về tìm x ∈ (0; 6) để hàm số y = f(x) = x(12 - 2x)2 có giá trị lớn nhất.
y' = 1(12 - 2x)2 + x.2.(12 - 2x).(-2)
12x2 - 96x + 144;
y' xác định ∀ x ∈ (0; 6)
Bảng biến thiên
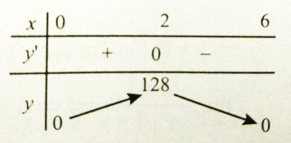
Hàm số đạt giá trị lớn nhất tại x=2
Câu 20: Khu chung cư Royal City có 250 căn hộ cho thuê. Nếu người ta cho thuê x căn hộ thì lợi nhuận hàng tháng, tính theo triệu đồng, được cho bởi:
P(x) = -8x2 + 3200x - 80000
Hỏi lợi nhuận tối đa họ có thể đạt được là bao nhiêu?
A. 150000 B. 220000 C. 292000 D. 250000
Ta có x ∈ (0; 250) ,P’(x) = -16x+3200.
Khi đó P’(x)=0 ⇔ -16x + 3200 = 0 ⇔ x = 200 (loại).
P(0)= - 8000; P(250) = 292 000
Do đó lợi nhuận tối đa họ thu được là P(250)=292000.
Câu 21: Một nhà máy sản xuất được 60000 sản phẩm trong một ngày và tổng chi phí sản xuất x sản phẩm được cho bởi:
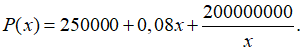
Hỏi nhà máy nên sản xuất bao nhiêu sản phẩm mỗi ngày để chi phí sản xuất là nhỏ nhất?
A. 30000 B. 40000 C. 50000 D.60000
Ta có x ∈ (0; 60000)
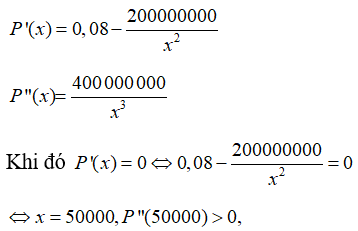
Do đó, hàm số đạt cực tiểu tại x = 50000.
Nên x=50000 là số sản phẩm cần sản xuất mỗi ngày để tối thiểu chi phí.
Câu 22: Tìm giá trị lớn nhất của hàm số y=x3−2x2−7x+1 trên đoạn [-2;1]
A. 3. B. 4.
C. 5. D. 6.
Câu 23: Cho hàm số y=f(x) liên tục trên ℝ và có bảng biến thiên
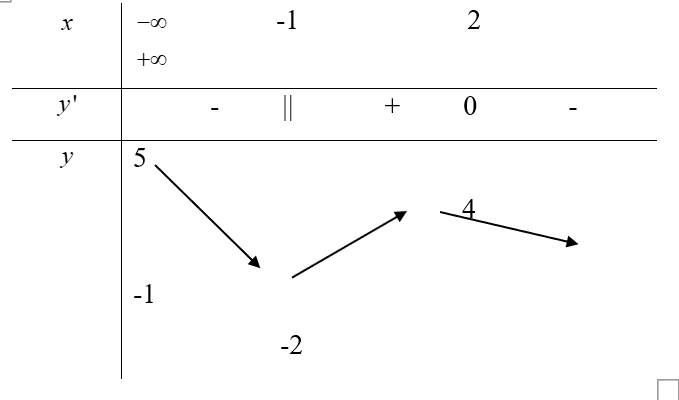
Khẳng định nào sau đây sai?
A. Hàm số không có giá trị lớn nhất và có giá trị nhỏ nhất bằng – 2.
B. Hàm số có hai điểm cực trị.
C. Đồ thị hàm số có hai tiệm cận ngang.
D. Hàm số có giá trị lớn nhất bằng 5 và giá trị nhỏ nhất bằng – 2.
Câu 24: Hàm số y=(4−x2)2+1 có giá trị lớn nhất trên đoạn [-1;1] là
A. 10. B. 12.
C. 14. D. 17.
Câu 25: Giá trị nhỏ nhất của hàm số y=x3−3x+5 trên đoạn [2;4] là
A. min[2;4]y=3. B. min[2;4]y=7.
C. min[2;4]y=5. D. min[2;4]y=0.
Câu 26: Giá trị lớn nhất của hàm số y=−x2−4x trên đoạn [32;4]
A. – 2. B. – 4.
C. −256. D. – 5.
Câu 27: Giá trị nhỏ nhất của hàm số y=x3−3x+1 trên đoạn [-1;4] là
A. 3. B. – 1.
C. – 4. D. 1.
Câu 28: Tìm giá trị nhỏ nhất của hàm số y=x−2x+1 trên đoạn [0;2] là
A. – 3. B. – 2.
C. 0. D. 2.
Câu 29: Hàm số f(x)=√2x−x2. Biết rằng hàm số f(x) đạt giá trị lớn nhất tại duy nhất điểm xo. Tìm xo.
A. xo=2. B. xo=0
C. xo=1 D. xo=12.
Câu 30: Cho hàm số y = x2 - 2|x| + 2 và các mệnh đề
(1) Hàm số trên liên tục trên R
(2) Hàm số trên có đạo hàm tại x = 0
(3) Hàm số trên đạt GTNN tại x = 0.
(4) Hàm số trên đạt GTLN tại x = 0.
(5) Hàm số trên là hàm chẵn
(6) Hàm số trên cắt trục hoành tại duy nhất một điểm
Trong các mệnh đề trên, số mệnh đề đúng là
A.1 B. 2 C.3 D. 4
* Hàm số đã cho liên tục trên R vì với ![]() nên (1) đúng
nên (1) đúng
* Tại điểm x = 0 hàm số không có đạo hàm nên (2) sai.
*y = x2 - 2|x| + 2 = |x|2 - 2|x| + 2 = (|x| - 1)2 + 1 ≥ 1 ∀ x
Suy ra, GTNN của hàm số là 1 khi |x| = 1 ⇔ x = ±1
nên hàm số không có GTLN.
* Phương trình x2 - 2|x| + 2=0 vô nghiệm nên đồ thị không cắt trục hoành.
f(-x)=(-x)2 - 2|-x| + 2 = x2 - 2|x| + 2 = f(x)
Nên hàm số đã cho là hàm số chẵn.
Mệnh đề 1, 5 đúng. Mệnh đề 2, 3,4,6 sai.
Câu 31: Cho hàm số y = -x4 + 2x2 - 1. Số giao điểm của đồ thị hàm số với trục Ox là:
A. 1 B.2 C. 3 D. 4
Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là:
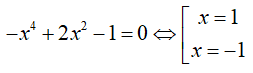
Số giao điểm của đồ thị hàm số với trục Ox là hai điểm.
Câu 32: Cho hàm số y = 3sinx - 4sin3x. Giá trị lớn nhất của hàm số trên khoảng (-π/2 ; π/2) bằng
A. -1 B. π/6 C. 1 D. -π/6
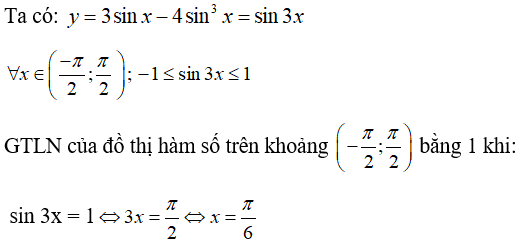
Câu 33: Tìm giá trị lớn nhất của m để hàm số y = x3 + 3x2 - mx - 4 đồng biến trên khoảng R?
A. m = -3 B. m < -3 C. m = 3 D. m ≥ 3
y' = 3x2 + 6x - m
Để hàm số đã cho đồng biến trên R khi và chỉ khi:
y' = 3x2 + 6x - m ≥ 0 ∀ x ∈ R
⇔ Δ = 9 + 3m ≤ 0 ⇔ m ≤ -3
Vậy giá trị lớn nhất của m để hàm số đã cho đồng biến trên R là m = -3.
Chọn A.
Câu 34: Giá trị nhỏ nhất của hàm số
![]()
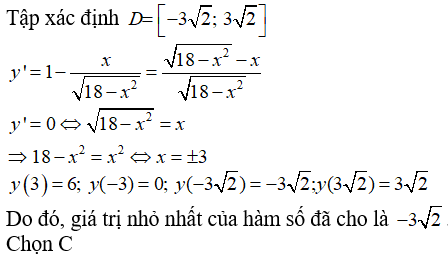
Câu 35: Giá trị lớn nhất của hàm số
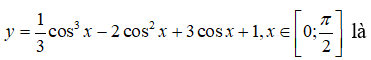
A. 1 B. 7/3 C. 2 D. 1/3
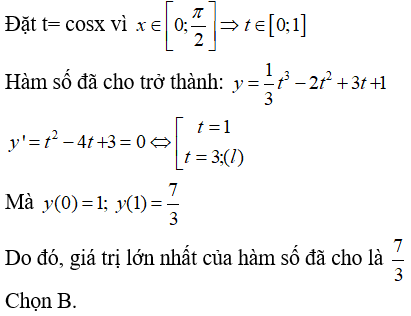
Câu 36: Giá trị nhỏ nhất của hàm số
![]()
A. 2√ - 2 B. 9/10 C. 2√2 - 1 D. 1 - 2√2

Câu 37: Tìm m để giá trị nhỏ nhất của
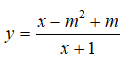
trên đoạn [0; 1] bằng -2
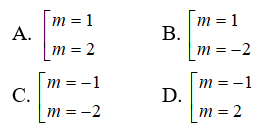
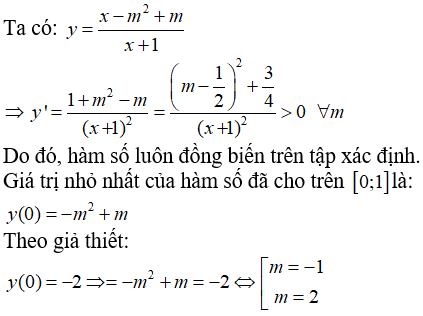
Câu 38: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x3 - 3x2 - 9x + 35 trên đoạn [-4; 4]
Hàm số f(x) liên tục trên [-4; 4]
Ta có f'(x) = 3x2 - 6x - 9; f'(x) = 0 ⇔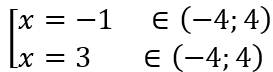
f(-4) = -41; f(-1) = 40; f(3) = 8;f(4) = 15.
Do đó 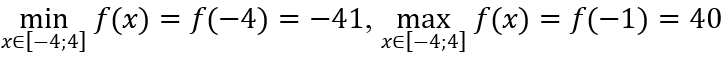
Câu 39: Cho hàm số f(x) = x3 + (m2 + 1)x + m2 - 2 với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 2] bằng 7.
A. m = ±1. B. m = ±√7. C. m = ±√2. D. m = ±3.
Đáp án : D
Giải thích :
Đạo hàm f'(x) = 3x2 + m2 + 1 > 0,∀ x ∈ R.
Suy ra hàm số f(x) đồng biến trên [0; 2] →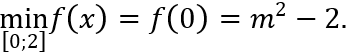
Theo bài ra: 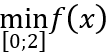 f(x) = 7 ⇔ m2 - 2 = 7 ⇔ m = ±3.
f(x) = 7 ⇔ m2 - 2 = 7 ⇔ m = ±3.
Câu 40: Cho hàm số 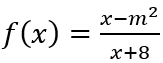 với m là tham số thực. Tìm giá trị lớn nhất của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 3] bằng -2.
với m là tham số thực. Tìm giá trị lớn nhất của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 3] bằng -2.
A. m = 4. B. m = 5. C. m = -4. D. m = 1.
Đáp án : A
Giải thích :
Đạo hàm 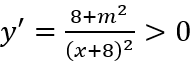 ,∀ x ∈ [0; 3].
,∀ x ∈ [0; 3].
Suy ra hàm số f(x) đồng biến trên đoạn 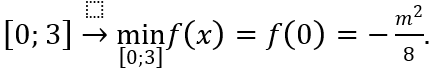
Theo bài ra: 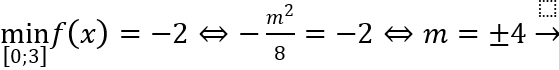 giá trị m lớn nhất là m = 4.
giá trị m lớn nhất là m = 4.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.