Toptailieu.vn biên soạn và giới thiệu cách giải các dạng toán về Giá trị lớn nhất và giá trị nhỏ nhất của hàm số môn Toán lớp 12 Giải tích gồm phương pháp giải chi tiết, bài tập minh họa có lời giải và bài tập tự luyện chi tiết giúp học sinh ôn tập và nắm chắc kiến thức các dạng toán. Mời các bạn đón xem:
300 Bài tập Giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đáp án (2023)
Dạng 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
A. Phương pháp giải & Ví dụ
1. Định nghĩa: Cho hàm số y = f(x) xác định trên miền D
Số M gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu: 
Kí hiệu: 
Số m gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu: 
Kí hiệu: 
2. Quy trình tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sử dụng bảng biến thiên
Bước 1. Tính đạo hàm f'(x).
Bước 2. Tìm các nghiệm của f'(x) và các điểm f'(x)trên K.
Bước 3. Lập bảng biến thiên của f(x) trên K.
Bước 4. Căn cứ vào bảng biến thiên kết luận 
3. Quy trình tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số không sử dụng bảng biến thiên
Trường hợp 1. Tập K là đoạn [a; b]
Bước 1. Tính đạo hàm f'(x).
Bước 2. Tìm tất cả các nghiệm xi ∈[a; b] của phương trình f'(x) = 0 và tất cả các điểm αi ∈ [a; b] làm cho f'(x) không xác định.
Bước 3.Tính f(a), f(b), f(xi), f(αi).
Bước 4. So sánh các giá trị tính được và kết luận 
Trường hợp 2. Tập K là khoảng (a; b)
Bước 1. Tính đạo hàm f'(x).
Bước 2. Tìm tất cả các nghiệm xi ∈ (a; b) của phương trình f'(x) = 0 và tất cả các điểm αi ∈ (a; b) làm cho f'(x) không xác định.
Bước 3. Tính 
Bước 4. So sánh các giá trị tính được và kết luận 
Chú ý: Nếu giá trị lớn nhất (nhỏ nhất) là A hoặc B thì ta kết luận không có giá trị lớn nhất (nhỏ nhất).
Ví dụ 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x3 - 3x2 - 9x + 2 trên đoạn [-2; 2].
Hướng dẫn
Ta có: y' = 3x2 - 6x - 9 = 0 ⇔
Mà y(-2) = 0; y(2) = -20; y(-1) = 7.
Suy ra 
Ví dụ 2: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 
Hướng dẫn
Tập xác định: D = [-2; 2]. Ta có: 
Khi đó y' = 0 ⇔ 
Có y(√2) = 2√2, y(2) = 2 ,y(-2) = -2.
Vậy 
Ví dụ 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x - sin2x trên đoạn [π/2; π]
Hướng dẫn
Ta có y' = 1 - 2cos2x = 0 ⇔ cos2x = 1/2 = cos π/3 ⇔ x = ±π/6 + kπ.
Xét x ∈[(-π)/2; π] ta được x = ±π/6; x = 5π/6.
f((-π)/2) = -π/2; f(π) = π; f((-π)/6) = -π/6 + √3/2; f(π/6) = π/6 - √3/2; f(5π/6) = 5π/6 + √3/2.
Suy ra 
B. Bài tập vận dụng
Câu 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x3 - 3x2 - 9x + 35 trên đoạn [-4; 4]
Hàm số f(x) liên tục trên [-4; 4]
Ta có f'(x) = 3x2 - 6x - 9; f'(x) = 0 ⇔
f(-4) = -41; f(-1) = 40; f(3) = 8;f(4) = 15.
Do đó 
Câu 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số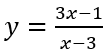 
trên [0; 2]
Hàm số đã cho xác định và liên tục trên đoạn [0; 2].
Ta có 
Tính y(0) = 1/3; y(2) = -5.
Suy ra 
Câu 3: Gọi m là giá trị nhỏ nhất của hàm số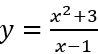 
trên đoạn [2; 4]. Tìm m.
Hàm số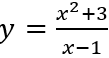 
liên tục trên đoạn [2;4].
Ta có 
Tính y'(2) = 7; y'(4) = 19/3; y'(3) = 6.
Suy ra m = 6.
Câu 4: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số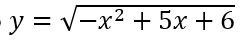 
trên đoạn [-1; 6]
Hàm số đã cho xác định và liên tục trên đoạn [-1; 6].
Ta có: 
y' = 0 ⇔ x = 5/2 ∈[-1; 6].
y(-1) = y(6) = 0, y(5/2) = 7/2.
Vậy 
Câu 5: Tìm tổng giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) = |x| + 3 trên [-1; 1]
Ta có 
Ta có bảng biến thiên của hàm số đã cho.
Vậy 
Câu 1: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = -2x4 + 4x2 + 5 trên đoạn [0; 2] là:
A. 
B. 
C.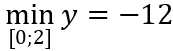 
và không có giá trị lớn nhất
D.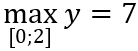 
và không có giá trị nhỏ nhất
Đáp án : B
Giải thích :
Ta có y' = -8x3 + 8x ; y' = 0 
Vì y(0) = 5; y(1) = 7; y(2) = -11 nên 
Câu 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x3 - 3x + 3 trên [-1; 3/2] lần lượt là;
A. 15/8 và 5
B. 5 và 1
C. 1 và 15/8
D. 5 và 15/8
Đáp án : B
Giải thích :
Ta có 
Vì y(-1) = 5; y(1) = 1; y(3/2) = 15/8 nên 
Câu 3: Giá trị nhỏ nhất của hàm số y = x - 5 + 4/x trên đoạn [1; 3] là:
A. 
B. 
C. 
D. 
Đáp án : A
Giải thích :
ĐKXĐ: x ≠ 0; 
Có y(1) = 0; y(2) = -1; y(3) = -2/3 nên 
Câu 4: Giá trị lớn nhất của hàm số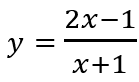 
trên đoạn [0;2] là:
A. 
B. 
C. 
D. 
Đáp án : B
Giải thích :
Câu 5: Giá trị nhỏ nhất của hàm số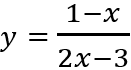 
trên [0;2] là:
A. 0
B. -1/3
C. -1
D. 2
Đáp án : B
Giải thích :
Ta có 
Dạng 2: Tìm m để hàm số có Giá trị lớn nhất, Giá trị nhỏ nhất thoả mãn điều kiện
A. Phương pháp giải & Ví dụ
Ví dụ 1: Tìm giá trị thực của tham số a để hàm số y = -x3 - 3x2 + a có giá trị nhỏ nhất trên đoạn [-1; 1] bằng 0.
Hướng dẫn
Đạo hàm f'(x) = -3x2 - 6x ⇒ f'(x) = 0 ⇔
Ta có 
Theo bài ra: 
Ví dụ 2: Cho hàm số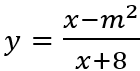 
với m là tham số thực. Tìm giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 3] bằng -2.
Hướng dẫn
TXĐ: D = R\{-8}.
Ta có 
Khi đó 
Ví dụ 3: Cho hàm só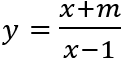 
(với m là tham số thực). Tìm các giá trị của m đề hàm số thỏa mãn 
Hướng dẫn
B. Bài tập vận dụng
Câu 1: Cho hàm số f(x) = x3 + (m2 + 1)x + m2 - 2 với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 2] bằng 7.
Đạo hàm f'(x) = 3x2 + m2 + 1 > 0,∀ x ∈ R.
Suy ra hàm số f(x) đồng biến trên 
Theo bài ra: 
Câu 2: Cho hàm số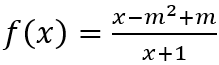 
với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 1] bằng -2.
Đạo hàm 
Suy ra hàm số f(x) đồng biến trên 
Theo bài ra: 
Câu 3: Tìm tất cả giá trị của m để giá trị nhỏ nhất của hàm số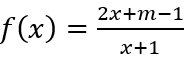 
trên đoạn [1; 2] bằng 1.
Ta có 
Nếu m < 3: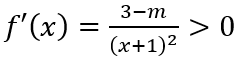 
nên hàm số đồng biến trên (1; 2)
(nhận).
Nếu m > 3: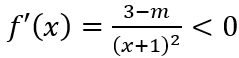 
nên hàm số nghịch biến trên (1; 2)
Câu 4: Tìm các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y = |x2 - 2x + m| trên đoạn [-1; 2] bằng 5.
Xét hàm số f(x) = x2 - 2x + m trên đoạn [-1; 2], ta có f'(x) = 2(x - 1)
và f'(x) = 0 ⇔ x = 1.
Vậy:
TH1. 
TH2. 
TH3. 
Câu 5: Cho hàm số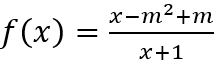 
với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 1] bằng -2.
Đạo hàm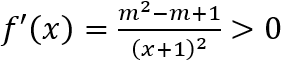 
,∀ x ∈[0; 1].
Suy ra hàm số f(x) đồng biến trên [0;1] 
Theo bài ra:
Câu 1: Cho hàm số f(x) = x3 + (m2 + 1)x + m2 - 2 với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 2] bằng 7.
A. m = ±1. B. m = ±√7. C. m = ±√2. D. m = ±3.
Đáp án : D
Giải thích :
Đạo hàm f'(x) = 3x2 + m2 + 1 > 0,∀ x ∈ R.
Suy ra hàm số f(x) đồng biến trên [0; 2] →
Theo bài ra: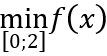 
f(x) = 7 ⇔ m2 - 2 = 7 ⇔ m = ±3.
Câu 2: Cho hàm số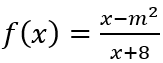 
với m là tham số thực. Tìm giá trị lớn nhất của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 3] bằng -2.
A. m = 4. B. m = 5. C. m = -4. D. m = 1.
Đáp án : A
Giải thích :
Đạo hàm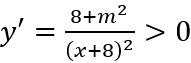 
,∀ x ∈ [0; 3].
Suy ra hàm số f(x) đồng biến trên đoạn 
Theo bài ra: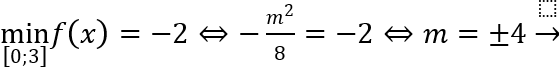 
giá trị m lớn nhất là m = 4.
Câu 3: Cho hàm số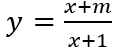 
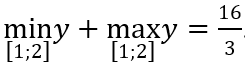
. Với tham số m bằng bao nhiêu thì thỏa mãn 
.
A. m = 0. B. m = 2. C. m = 4. D. m = 5.
Đáp án : D
Giải thích :
Đạo hàm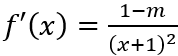 
.
Suy ra hàm số f(x) là hàm số đơn điệu trên đoạn [1; 2] với mọi m ≠ 1.
Khi đó
Câu 4: Cho hàm số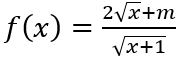 
với m là tham số thực. Tìm tất cả các giá trị của m > 1 để hàm số có giá trị lớn nhất trên đoạn [0; 4] nhỏ hơn 3.
A. m ∈ (1; 3). B. m ∈ (1; 3√5 - 4). C. m ∈ (1; √5). D. m ∈ (1; 3].
Đáp án : C
Giải thích :
Đạo hàm 
Lập bảng biến thiên, ta kết luận được 
Vậy ta cần có 
Câu 5: Cho hàm số y = x3 - 3x + 1 . Tìm tìm tập hợp tất cả giá trị m > 0, để giá trị nhỏ nhất của hàm số trên D = [m + 1; m + 2] luôn bé hơn 3 là:
A. (0; 1). B. (1/2; 1) C. (-∞; 1)\{-2} D. (0; 2).
Đáp án : A
Giải thích :
Ta có : 
Hàm số đồng biến trên khoảng (1; +∞).
Trên D =[m + 1; m + 2], với m > 0 , ta có :
Ycbt 
Kết hợp điều kiện Suy ra m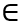 
(0; 1)
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
