Toptailieu.vn biên soạn và giới thiệu cách giải các dạng toán về Cực trị của hàm số môn Toán lớp 12 Giải tích gồm phương pháp giải chi tiết, bài tập minh họa có lời giải và bài tập tự luyện chi tiết giúp học sinh ôn tập và nắm chắc kiến thức các dạng toán. Mời các bạn đón xem:
300 Bài tập Cực trị của hàm số có đáp án (2023)
Dạng 1: Tìm cực trị của hàm số
A. Phương pháp giải & Ví dụ
1.Định nghĩa: Cho hàm số y = f(x)xác định và liên tục trên khoảng (a;b) (có thể a là -∞; b là +∞) và điểm x0∈(a;b).
Nếu tồn tại số h > 0 sao cho f(x)< f(x0 ) với mọi x ∈ (x0 - h;x0 + h) và x≠x_0 thì ta nói hàm số f(x) đạt cực đại tại x0.
Nếu tồn tại số h >0 sao cho f(x) >f(x0 ) với mọi x ∈ (x0 - h;x0 + h) và x ≠ x0 thì ta nói hàm số f(x) đạt cực tiểu tại x0.
2.Điều kiện đủ để hàm số có cực trị: Giả sử hàm số y=f(x) liên tục trên
K=(x0 - h;x0 + h)và có đạo hàm trên K hoặc trên K\{x0}, với h >0.
Nếu f'(x)> 0 trên khoảng (x0 - h;x0) và f'(x) <0 trên (x0;x0 + h) thì x0 là một điểm cực đại của hàm số f(x).
Nếu f'(x) < 0 trên khoảng (x0 - h;x0) và f'(x) >0 trên (x0;x0+ h) thì x0 là một điểm cực tiểu của hàm số f(x).
Minh họa bằng bảng biến thiến
Chú ý.
Nếu hàm sốy=f(x) đạt cực đại (cực tiểu) tại x0 thì x0 được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x0) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là fCÑ (fCT), còn điểm M(x0;f(x0)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
3.Quy tắc tìm cực trị của hàm số
Quy tắc 1:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tínhf'(x). Tìm các điểm tại đó f'(x)bằng 0 hoặc f'(x) không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.
Quy tắc 2:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính f'(x). Giải phương trình f'(x)và ký hiệuxi (i=1,2,3,...)là các nghiệm của nó.
Bước 3. Tính f''(x) và f''(xi ) .
Bước 4. Dựa vào dấu của f''(xi )suy ra tính chất cực trị của điểm xi.
Ví dụ 1. Tìm cực trị của hàm số y = 2x3 - 6x + 2.
Hướng dẫn
Tập xác định D = R.
Tính y' = 6x2 - 6. Cho y'= 0 ⇔ 6x2 - 6 = 0 ⇔ x = ±1.
Bảng biến thiên
Vậy hàm số đạt cực đại tại x = - 1, y = 6 và hàm số đạt cực tiểu tại x = 1,y = -2.
Ví dụ 2. Tìm cực trị của hàm số y = x4 - 2x2 + 2.
Hướng dẫn
Tập xác định D = R.
Tính y' = 4x3 - 4x. Cho y'= 0 ⇔ 4x3 - 4x = 0 ⇔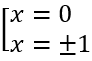
.
Bảng biến thiên
Vậy hàm số đạt cực tiểu tại x = ±1, y = 1 và hàm số đạt cực đại tại x = 0, y = 2.
Ví dụ 3. Tìm cực trị của hàm số y = 
Hướng dẫn
Tập xác định D = R\{2}. Tính 
Bảng biến thiên
Vậy hàm số đã cho không có cực trị.
B. Bài tập vận dụng
Bài 1. Tìm cực trị của hàm số y = -x3 + 3x2 - 4
Tập xác định D = R.
Tính y'= -3x2 + 6x.
Cho y'= 0⇔-3x2 + 6x = 0⇔
Bảng biến thiên
Vậy hàm số đạt cực tiểu tại x = 0,y = -4 và hàm số đạt cực đại tại x = 2,y = 0.
Bài 2. Tìm cực trị của hàm số y = -x3 + 3x3 - 3x + 2
Tập xác định D = R.
Tính y' = -3x2 + 6x-3.
Cho y'= 0 ⇔ -3x2+ 6x-3 = 0 ⇔ x = 1.
Bảng biến thiên
Vậy hàm số đã cho không có cực trị.
Bài 3. Gọi A,B là hai điểm cực trị của đồ thị hàm số y = 2x3 - 3x2 - 12x + 1. Tìm tọa độ A,B và phương trình đường thẳng qua hai điểm đó.
Tập xác định D = R.
Tính y' = 6x2 - 6x - 12.
Cho y'= 0 ⇔
Bảng biến thiên
Suy ra tọa độ hai điểm cực trị là A(-1;8), B(2;-19).
Vậy phương trình đường thẳng AB là 9x + y + 1 = 0.
Bài 4. Cho hàm số y = x3 - 3x2 có đồ thị (C). Tìm các điểm cực đại, cực tiểu của đồ thị (C)và khoảng cách giữa hai điểm cực trị đó.
Tập xác định D = R.
Tính y'= 3x2-6x.
Cho y'= 0 ⇔
Bảng biến thiên
Vậy tọa độ hai điểm cực trị là A(-1;8),B(2;-19). Khi đó AB =
Bài 5. Tìm cực trị của hàm số y = x4/4 - x2 + 2
Tập xác định D = R.
Tính y'= 2x3-2x.
Cho y'= 0 ⇔ 4x3 - 4x = 0 ⇔
Bảng biến thiên
Vậy hàm số đạt cực tiểu tại x = ±1, y = 3/2 và hàm số đạt cực đại tại x = 0, y = 2.
Câu 1: Cho hàm số y = f(x) có đồ thị như hình vẽ:
Đồ thị hàm số y = f(x) có mấy điểm cực trị?
A. 2. B. 1. C. 0. D. 3.
Câu 2: Cho hàm số y = x3 - 3x2 + 2 . Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại x = 2 và đạt cực tiểu tại x = 0.
B. Hàm số đạt cực tiểu tại x = 2 và đạt cực đại x = 0.
C. Hàm số đạt cực đại tại x = -2và cực tiểu tại x = 0.
D. Hàm số đạt cực đại tại x = 0và cực tiểu tại x = -2.
Đáp án : B
Giải thích :
y' = 3x2 - 6x = 0 ⇔ 
Lập bảng biến thiên ta được hàm số đạt cực đại tại x = 2 và đạt cực tiểu tại x = 0
Câu 3: Cho hàm số y = x4 - 2x2 + 3 . Khẳng định nào sau đây là đúng?
A. Hàm số có ba điểm cực trị. B. Hàm số chỉ có đúng 2 điểm cực trị.
C. Hàm số không có cực trị. D. Hàm số chỉ có đúng một điểm cực trị.
Đáp án : A
Giải thích :
y' = 4x3 - 4x = 0 ⇔
y(0) = 3; y(1) = y(-1) = 2 nên hàm số có hai cực trị.
Câu 4: Gọi M, n lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số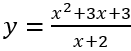 
. Khi đó giá trị của biểu thức M2 - 2n bằng:
A. 8. B. 7. C. 9. D. 6.
Đáp án : B
Giải thích :
Hàm số đạt cực đại tại x = -3 và yCD = -3
Hàm số đạt cực tiểu tại x = -1 và yCT = 1
⇒ M2 - 2n = 7
Phương pháp trắc nghiệm:
Bấm máy tính:
Bước 1:
Bước 2: Giải phương trình bậc hai :
Bước 3: Nhập vào máy tính 
Caclx = A → C
Caclx = B → D
Bước 4: Tính C2 - 2D = 7
Câu 5: Cho hàm số y = x3 + 17x2 - 24x + 8 . Kết luận nào sau đây là đúng?
A. xCD = 1. B. xCD = 2/3. C. xCD = -3. D. xCD = -12.
Đáp án : D
Giải thích :
y' = 3x2 + 34x - 24 = 0 ⇔ 
Lập bảng biến thiên ta thấy hàm số đạt cực đại tại x = -12 .
Dạng 2: Tìm tham số m để hàm số đạt cực trị tại một điểm
A. Phương pháp giải & Ví dụ
Trong dạng toán này ta chỉ xét trường hợp hàm số có đạo hàm tại x0.
Khi đó để giải bài toán này, ta tiến hành theo hai bước.
Bước 1. Điều kiện cần để hàm số đạt cực trị tại x0 là y'(x0) = 0, từ điều kiện này ta tìm được giá trị của tham số .
Bước 2. Kiểm lại bằng cách dùng một trong hai quy tắc tìm cực trị ,để xét xem giá trị của tham số vừa tìm được có thỏa mãn yêu cầu của bài toán hay không?
Ví dụ 1. Cho hàm số y = x3 - 3mx2 +(m2 - 1)x + 2, m là tham số thực. Tìm tất cả các giá trị của m để hàm số đã cho đạt cực tiểu tại x = 2.
Hướng dẫn
Tập xác định D = R.
Tính y'=3x2 - 6mx + m2 - 1; y'' = 6x - 6m.
Hàm số đã cho đạt cực tiểu tại x = 2 ⇒ 
⇔ m = 1.
Ví dụ 2. Tìm các giá trị của m để hàm số y = -x3 + (m+3)x2 - (m2 + 2m)x - 2 đạt cực đại tại x = 2.
Hướng dẫn
Tập xác định D = R.
y' = -3x2 + 2(m + 3)x - (m2 + 2m)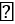 
; y'' = -6x + 2(m + 3).
Hàm số đã cho đạt cực đại tại x = 2 
Kết luận : Giá trị m cần tìm là m = 0 ,m = 2.
Ví dụ 3. Tìm m để hàm số y = x4 - 2(m + 1)x2 - 2m - 1 đạt cực đại tại x = 1 .
Hướng dẫn
Tập xác định D = R.
Ta có y' = 4x3 -4(m + 1)x.
+ Để hàm số đạt cực đại tại x = 1 cần y'(1) = 0 ⇔ 4 - 4(m + 1) = 0 ⇔ m = 0
+ Với m = 0 ⇒ y' = 4x3 - 4x ⇒ y'(1) = 0.
+ Lại có y'' = 12x2 - 4 ⇒ y''(1) = 8 > 0.
⇒Hàm số đạt cực tiểu tại x = 1 ⇒ m = 0 không thỏa mãn.
Vậy không có giá trị nào của m để hàm số đạt cực đại tại x = 1.
B. Bài tập vận dụng
Bài 1. Cho hàm số: y = 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x = 1
TXĐ: D = R
Ta có: y' = x2 - 2mx + m2 - m + 1, y'' = 2x - 2m
Điều kiện cần: y'(1) = 0 ⇔ m2 - 3m + 2 = 0 ⇔ m = 1 hoặc m = 2
Điều kiện đủ:
Với m = 1 thì y''(1) = 0 ⇒ hàm số không thể có cực trị.
Với m = 2 thì y''(1) = -2 < 0 ⇒ hàm số có cực đại tại x = 1 .
Vậy m = 2 là giá trị cần tìm.
Bài 2. Cho hàm số y = 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x = -2 .
♦ Tập xác định: D = R
♦ Đạo hàm: y' = x2 + 2(m2 - m + 2)x + 3m2 + 1
Điều kiện cần:
Hàm số đạt cực tiểu tại x = -2 ⇒ y'(-2) = 0
Điều kiện đủ:
Với m = 1, ta có: y' = x2 + 4x + 4, y' = 0 ⇔ x = -2
Lập BBT ta suy ra m = 1 không thỏa.
Với m = 3, ta có: y' = x2 + 16x + 28, y' = 0 ⇔
Lập BBT ta thấy hàm số đạt cực tiểu tại x = -2.
♦ Vậy giá trị m cần tìm là m = 3.
Bài 3. Cho hàm số y = 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x = 2.
Tập xác định D = R.
Tính y' = x2 –2(m + 1)x + m2 + 2m; y'' = 2x – 2m - 2.
Để hàm số đã cho đạt cực tiểu tại x = 2 
Vậy m = 0 là giá trị cần tìm.
Bài 4. Tìm tất cả tham số thực m để hàm số y = (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tại
x = -1.
Tập xác định D = R.
Tính y' = 4(m - 1)x3 – 2(m2 - 2)x; y'' = 12(m - 1)x2 – 2m2 + 4.
Để hàm số đã cho đạt cực đại tại x = -1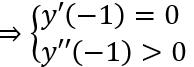 
⇔
.
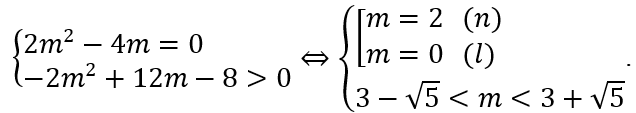
Vậy m = 2 là giá trị cần tìm.
Bài 5. Tìm giá trị của tham số m để hàm số y = x3/3 +(2m - 1)x2 + (m - 9)x + 1 đạt cực tiểu tại
x = 2 .
Ta có : y' = x2 + 2(2m - 1)x + m - 9.
Điều kiện cần để hàm số đạt cực tiểu tại x = 2 là
y'(2) = 0 ⇒ 4 + 4(2m - 1) + m - 9 = 0 ⇒ m = 1.
Kiểm tra lại . Ta có y'' = 2x + 2(2m - 1).
Khi m = 1 thì y'' = 2x + 2, suy ra y''(2) = 6 > 0. Do đó hàm số đạt cực tiểu tại x = 2
Vậy hàm số đạt cực tiểu tại x = 2 ⇔ m = 1.
Câu 1. Với giá trị nào của tham số m thì hàm số y = 2(m2 - 3)sinx - 2msin2x + 3m - 1 đạt cực đại tại x = π/3.
A. Không tồn tại giá trị m. B. m = 1.
C. m = -3 D. m = -3, m = 1.
Đáp án : C
Giải thích :
Tập xác định D = R.
Tính y' = 2(m2 - 3)cosx - 4mcos2x; y'' =2(3 - m2 )sinx + 8msin2x.
Để hàm số đã cho đạt cực đại tại x = π/3 ta có
Vậy m = -3 là giá trị cần tìm.
Câu 2. Tìm tất cả các giá trị của tham số m để hàm số y = x2 - mx2 + (2m - 3)x - 3 đạt cực đại tại x = 1.
A. m = 3. B. m > 3. C. m ≤ 3. D. m < 3.
Đáp án : B
Giải thích :
+ Để hàm số đạt cực đại x = 1thì 
Câu 3. Hàm số y = asin2x + bcos3x - 2x (0 < x < 2π) đạt cực trị tại x = π/2; x = π. Khi đó, giá trị của biểu thức P = a + 3b - 3ab là:
A. 3. B. -1. C. 1. D. -3.
Đáp án : C
Giải thích :
TXĐ: D = R
+ Ta có: y' = 2acos2x - 3bsin3x - 2.
Hàm số đạt cực trị tại x = π/2; x = π nên ta có hệ phương trình:
Do đó, giá trị của biểu thức P = a + 3b - 3ab = 1.
Câu 4. Hàm số y = x3 - 3x2 + mx - 2 đạt cực tiểu tại x = 2 khi?
A. m > 0. B. m ≠ 0. C. m = 0. D. m < 0.
Đáp án : C
Giải thích :
y' = 3x2 - 6x + m
y''= 6x - 6 )
Hàm số đạt cực tiểu tại x = 2 khi:
Câu 5. Biết đồ thị hàm số y = x3 - 2x2 + ax + b có điểm cực trị là A(1;3). Khi đó giá trị của 4a - b là:
A. 1. B. 2. C. 3. D. 4.
Đáp án : A
Giải thích :
Ta có y' = 3x2 - 4x + a
Đồ thị hàm số có điểm cực trị là A(1;3), ta có:
Khi đó ta có, 4a - b = 1.
Dạng 3: Biện luận theo m số cực trị của hàm số
1. Cực trị của hàm số bậc ba
Cho hàm số y = ax3 + bx2 + cx + d, a ≠ 0.
y' = 0 ⇔ 3ax2 + 2bx + c = 0 (1) ; Δ'y' = b2 - 3ac
Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.
Hàm số bậc 3 không có cực trị ⇔ b2 - 3ac ≤ 0
Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.
Hàm số bậc 3 có 2 cực trị ⇔ b2 - 3ac > 0
2. Cực trị của hàm số bậc bốn trùng phương
Cho hàm số: y = ax4 + bx2 + c (a ≠ 0) có đồ thị là (C).
y' = 4ax3 + 2bx; y' = 0 ⇔ 
(C)có một điểm cực trị y' = 0 có 1 nghiệm x = 0 ⇔ -b/2a ≤ 0 ⇔ ab ≥ 0.
(C)có ba điểm cực trị y' = 0 có 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.
Ví dụ 1: Tìm m để hàm số y = x3 + mx + 2 có cả cực đại và cực tiểu.
Hướng dẫn
y' = 3x2 + m.
Hàm số y = x3 + mx + 2 có cả cực đại và cực tiểu khi và chỉ khi y'= 0 có hai nghiệm phân biệt.
Vậy m < 0.
Ví dụ 2: Cho hàm số y = (m - 2)x3 - mx - 2. Với giá trị nào của m thì hàm số có cực trị?
Hướng dẫn
Tập xác định D = R.
Tính y' = 3(m - 2)x2 - m.
Cho y' = 0 ⇔ 3(m - 2)x2 - m = 0 (1).
+ TH1: Xét m = 2 ⇒ y' = -2 < 0 ∀ x nên hàm số đã cho không có cực trị.
+ TH2: Xét m ≠ 2
Hàm số có cực trị khi Δ'> 0 ⇔ m(m - 2) > 0 ⇔
Vậy m > 2 ∨ m < 0.
Ví dụ 3: Xác định các giá trị của tham số m để đồ thị hàm số y = mx4 - m2 x2 + 2016 có 3 điểm cực trị?
Hướng dẫn
Tập xác định D = R.
Tính y' = 4mx3 - 2xm2.
Để hàm số có 3 điểm cực trị khi 
B. Bài tập vận dụng
Bài 1: Tìm m để hàm số y = mx3 + 3mx2 - (m - 1)x - 1 có cực trị.
TXĐ: D = R
Ta có: y' = 3mx2 + 6mx - m + 1. Hàm số có đạo hàm tại mọi điểm nên x0 là điểm cực trị của hàm số thì đạo hàm tại đó phải bằng 0.
Vậy hàm số có cực trị khi và chỉ khi y' = 0 phải có nghiệm và y' đổi dấu qua nghiệm đó.
* Nếu m = 0 ⇒ y' = 1 > 0 ∀ x ∈ R ⇒ hàm số không có cự trị
* Nếu m ≠ 0. Khi đó y' là một tam thức bậc hai nên y' = 0 có nghiệm và đổi dấu khi qua các nghiệm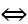 
y' = 0 có hai nghiệm phân biệt hay Δ' = 12m2 - 3m > 0 ⇔ m < 0 hoặc m > 1/4.
Vậy, với m < 0 hoặc m > 1/4 là những giá trị cần tìm.
Bài 2: Tìm m để hàm số y = x3 - 3(m - 1)x2 + 3(2m - 4)x + m có cực trị.
Ta có: y' = 3[x2 - 2(m - 1)x + 2m - 4]
Hàm số có cực trị 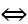y' = 0 có hai nghiệm phân biệt Δ' = m2 - 4m + 5 > 0 đúng với mọi m. Vậy hàm số luôn có cực trị với mọi m.
Bài 3: Tìm điều kiện của tham số m để hàm số y = x3 + mx2 +(4m + 3)x + 2m - 1 có hai điểm cực trị.
Tập xác định D = R.
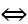
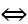
Tính y' = 3x2 + 2mx + 4m + 3; Hàm số có hai cực trị y' = 0 có hai nghiệm thực phân biệt và đổi dấu Δ' > 0 ⇔ m2 - 12m - 9 > 0 (khi đó y' đổi dấu qua nghiệm) ⇔ m ∈(-∞;6-3√5)∪(6+3√5;+∞).
Bài 4: Tìm các giá trị của m để hàm số y = x3 - 2mx + 4 không có điểm cực trị.
* Tập xác định D = R.
* Tính y' = 3x2 - 2m.
* Hàm số không có điểm cực trị khi phương trình y' = 0 vô nghiệm hoặc có nghiệm kép 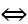x2 = 2m/3 ≤ 0 ⇔ m ≤ 0.
Bài 5: Tìm m để hàm số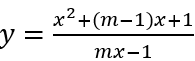 
có cực trị.
• Với m = 0 ta có y = -x2 + x - 1, ta thấy hàm số đạt cực đại tại x = 1/2. Suy ra m = 0 thỏa yêu cầu bài toán.
• m ≠ 0, ta có: 
Suy ra y' = 0 ⇔ mx2 - 2x + 1 - 2m = 0 (*)
Hàm số đã cho có cực trị khi và chỉ khi phương trình (*) có hai nghiệm phân biệt khác 1/m ⇔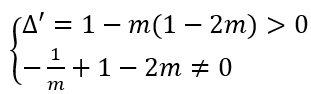 
⇔2m2 - m + 1 > 0 đúng với mọi m.
Vậy hàm số đã cho luôn có cực trị với mọi m.
Câu 1: Hàm số y = x4 + 2(m - 2)x2 + m2 - 2m + 3 có đúng 1 điểm cực trị thì giá trị của m là:
A. m ≥ 2. B. m < 2. C. m > 2. D. m = 2.
Đáp án : A
Giải thích :
+ Hàm trùng phương có 1 điểm cực trị khi ab ≥ 0 ⇔ m - 2 ≥ 0 ⇔ m ≥ 2.
Câu 2: Cho hàm số y = (m - 1)x3 - 3x2 - (m + 1)x + 3m2 - m + 2. Để hàm số có cực đại, cực tiểu thì:
A. m = 1. B. m ≠ 1. C. m > 1. D. m tùy ý.
Đáp án : B
Giải thích :
+ Hàm số có cực đại, cực tiểu khi 
Câu 3: Tìm tất cả các giá trị thực của mđể hàm số y = mx4 - (m + 1) x2 + 2m - 1 có 3 điểm cực trị ?
A.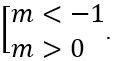 
B.m < -1. C.-1 < m < 0. D. m > -1.
Đáp án : A
Giải thích :
[Phương pháp tự luận]: y' = 4mx3 - 2(m + 1)x = 0
Hàm số có 3 điểm cực trị 
[Phương pháp trắc nghiệm] : Đồ thị hàm số y = ax4 + bx2 + c có 3 cực trị khi và chỉ khi a và b trái dấu , tức là : ab < 0
Suy ra :
Câu 4: Tìm tất cả các giá trị thực của m để hàm số y = x3 - 2x2 + (m + 3)x - 1 không có cực trị?
A. m ≥ -8/3. B. m > -5/3. C. m ≥ -5/3. D. m ≤ -8/3.
Đáp án : C
Giải thích :
[Phương pháp tự luận]
y' = 3x2 - 4x + m + 3
Hàm số không có cực trị 
Câu 5: Tìm tất cả các giá trị thực của tham số m để hàm số: y = 1/3 x3 + mx2 + (m + 6)x + m có cực đại và cực tiểu .
A. -2 < m < 3 . B.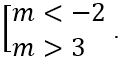
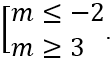
C.
D. -2 ≤ m ≤ 3.
Đáp án : B
Giải thích :
y' = x2 + 2mx + m + 6
Hàm số có cực đại và cực tiểu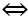 
y' = 0 có hai nghiệm phân biệt.
Dạng 4: Bài toán liên quan đến cực trị của hàm số
A. Phương pháp giải & Ví dụ
1. Cực trị của hàm số bậc ba
Hàm số có cực trị y' = 0 có hai nghiệm phân biệt .
Nếu hàm số y = ax3 + bx2 + cx + d(a ≠ 0) có hai điểm cực trị x1,x2 và
y = g(x).y^' + a.x + b thì đường thẳng đi qua hai điểm cực trị có phương trình y = ax + b và giá trị cực trị là của hàm số là y1 = a.x1+b; y2 = a.x2 + b
Tìm điều kiện cuả tham số để hàm số có cực trị thỏa mãn hệ thức cho trước
- Tìm điều kiện để hàm số có cực trị.
- Phân tích hệ thức để áp dụng vi-et cho phương trình bậc hai.
2. Cực trị của hàm số bậc bốn trùng phương
Cho hàm số: y = ax4 + bx2 + c (a ≠ 0) có đồ thị là (C).
(C)có ba điểm cực trị y' = 0 có 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.
Khi đó hàm số có 3 điểm cực trị thì 3 điểm cực trị là 0;
Tọa độ 3 điểm cực trị tương ứng của đồ thị hàm số là: 
Nhận xét: tam giác ABC cân tại A, có A ∈Oy ;
Tam giác ABC vuông tại 
hoặc ΔABC vuông cân tại A ⇔ BC2 = AB2 + AC2
Tam giác ABC đều 
hoặc ΔABC đều ⇔ BC2 = AB2
Đặc biệt: Tam giác ABC có một góc bằng 120° 
Bán kính đường tròn ngoại tiếp tam giác ABC là 
Bán kính đường tròn nội tiếp tam giác ABC là
Phương trình đường tròn ngoại tiếp ΔABC là:
Ví dụ 1. Cho hàm số y = x3 - 3(m + 1)x2 + 9x - 2m2 + 1 (C). Tìm giá trị của m để đồ thị hàm số (C) có cực đại, cực tiểu tại x1, x2 sao cho |x1 - xc | = 2
Hướng dẫn
Ta có y' = 0 ⇔ x2 - 2(m + 1)x + 3 = 0. ĐK có 2 điểm cực trị Δ' = (m + 1)2 - 3 > 0
Khi đó
Ví dụ 2. Cho hàm số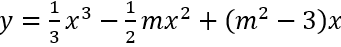 
(C). Tìm giá trị của m để đồ thị hàm số (C) có cực đại, cực tiểu tại x1,x2 sao cho x12 + x22 = 6
Hướng dẫn
Ta có y' = x2 - mx + m2 - 3. ĐK có 2 cực trị Δ = m2 - 4(m2 - 3) = 12 - 3m2 > 0
Khi đó 
Ví dụ 3. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số y = x4 - 2mx2 + 2m4 - m có ba điểm cực trị đều thuộc các trục tọa độ.
Hướng dẫn
Ta có y' = 4x3 - 4mx = 4x[x2 - m].
Hàm số đã cho có ba điểm cực trị khi và chỉ khi:
Khi đó ba điểm cực trị của đồ thị hàm số là:
A(0; 2m4 - m), B(-√m; 2m4 - m2 - m), C(√m; 2m4 - m2 - m)
Có A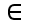 
Oy.Khi đó ba điểm cực trị đều thuộc các trục tọa độ
⇔ yB = 0 = yC ⇔ 2m4 - m2 - m = 0 ⇔ m = 1
B. Bài tập vận dụng
Câu 1:Cho hàm số y = 4x3 + mx2 - 3x + 1. Tìm tất cả các giá trị của m để hàm số có hai điểm cực trị x1,x2 thỏa x1 = -2x2
Ta có y' = 12x2 + 2mx - 3. ĐK có 2 cực trị là: Δ' = m2 + 36 > 0
Câu 2:Cho hàm số y = (m + 2)x3 + 3x2 + mx - 5, m là tham số. Tìm các giá trị của m để các điểm cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số dương.
Các điểm cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số dương
⇔ PT y' = 3(m + 2)x2 + 6x + m = 0 có 2 nghiệm dương phân biệt
Câu 3:Cho hàm số y = x3 + (1 - 2m)x2 + (2 - m)x + m + 2 (1). Tìm các giá trị của m để đồ thị hàm số (1) có điểm cực đại, điểm cực tiểu , đồng thời hoành độ của điểm cực tiểu nhỏ hơn 1.
y' = 3x2 + 2(1 - 2m)x + 2 - m = g(x)
YCBT ⇔ Phương trình y' = 0 có hai nghiệm phân biệt x1,x2thỏa mãn x1 < x2 < 1.
Câu 4:Cho hàm số y = x3 + 3x2 + mx + m - 2 (m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành.
f'(x) = 3x2 + 6x + m
Hàm số có hai cực trị khi và chỉ khi:f'(x) = 0 có hai nghiệm phân biệt
⇔ Δ = 9 - 3m > 0 ⇔ m < 3
Giả sử x1, x2 là nghiệm của phương trình f'(x) = 0 ta có
g(x1) = 2/3 (m - 3)(x1 + 1); g(x2) = 2/3 (m - 3)(x2 + 1)
Hai điểm cực trị của đồ thị hàm số nằm về hai phía của 
(g(x1). g(x2) < 0 ⇔ (m - 3)2 (x1 + 1)(x2 + 1) < 0⇔(m - 3)2 (x1 x2 + x1 + x2 + 1) < 0 ⇔(x1 x2 + x1 + x2 + 1) < 0 (m < 3) )
Vậy:(x1 x2 + x1 + x2 + 1) < 0 ⇔ m/3 - 1 < 0 ⇔ m < 3
Câu 5:Tìm các giá trị của tham số m để đồ thị hàm số y = 2x3 + 3(m - 3)x2 + 11 - 3m có hai điểm cực trị. Đồng thời hai điểm cực trị đó và điểmC(0; -1) thẳng hàng .
y' = 6x2 + 6(m - 3)x
Hàm số có 2 cực trị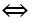 
m ≠ 3
Khi đó đồ thị hàm số đã cho có 2 điểm cực trị A(0; 11 - 3m)
Phương trình đt AB : (3 - m)2 x + y - 11 + 3m = 0
A,B,C thẳng hàng 
Hay : -1 - 11 + 3m = 0 ⇔ m = 4.
Câu 1: Tìm tất cả các giá trị thực của tham số m để hàm số y = m/3 x3 + 2x2 + mx + 1 có 2 điểm cực trị thỏa mãn xCĐ < xCT.
A. m < 2. B.-2 < m < 0. C. -2 < m < 2. D. 0 < m < 2.
Đáp án : D
Giải thích :
[Phương pháp tự luận]y' = mx2 + 4x + m
Câu 2: Tìm tất các giá trị thực của tham số m để hàm số y = 1/3 x3 + (m + 3)x2 + 4(m + 3)x + m3 - m đạt cực trị tại x1,x2 thỏa mãn -1 < x1 < x2.
A. -7/2 < m < -2. B. -3 < m < 1. C.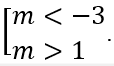 
D. -7/2 < m < -3.
Đáp án : D
Giải thích :
y' = x2 + 2(m + 3)x + 4(m + 3)
Yêu cầu của bài toán ⇔ y' = 0 có hai nghiệm phân biệt x1, x2 thỏa mãn:
-1 < x1 < x2.
Câu 3: Tìm các giá trị của tham sốmđể hàm số: y = 1/3 mx3 - (m - 1)x2 + 3(m - 2)x + 1/6 đạt cực trị tại x1,x2_2 thỏa mãn x2 + 2x2 = 1.
A. 1 - √6/2 < m < 1 + √6/2. B. 
C.m ∈(1 - √6/2; 1 + √6/2) \ {0}. D. m = 2.
Đáp án : B
Giải thích :
y' = mx2 - 2(m - 1)x + 3(m - 2)
Yêu cầu của bài toán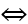 
y' = 0 có hai nghiệm phân biệt x1; x2 thỏa mãn:
x1 + 2x2 = 1.
Câu 4: Tìm các giá trị của tham sốm để đồ thị hàm số: y = x4 -2m2x2 + 1 có ba điểm cực trị là ba đỉnh của một tam giác vuông cân.
A. m = -1. B. m ≠ 0. C. m = 1. D. m = ±1.
Đáp án : D
Giải thích :
y' = 4x3 - 4m2 x
y' = 0 ⇔ 4x(x2 - m2) = 0)
Hàm số có 3 điểm cực trị 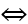m ≠ 0
Khi đó 3 điểm cực trị của đồ thị hàm số là : A(0; 1), B(m; 1 - m4 ), C(-m; 1 - m4 )
Do tính chất đối xứng, ta có ΔABC cân tại đỉnh A .
Vậy ΔABC chỉ có thể vuông cân tại đỉnh 
Kết hợp điều kiện ta có: m = ±1 ( thỏa mãn).
Lưu ý: có thể sử dụng công thức b3/8a + 1 = 0.
Câu 5: Tìm các giá trị của tham sốm để đồ thị hàm số: y = x4 - 2(m + 1)x2 + m2 có ba điểm cực trị là ba đỉnh của một tam giác vuông cân.
A. Không tồn tại m. B. m = 0. C.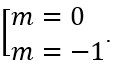
D.m = -1.
Đáp án : B
Giải thích :
y' = 4x3 - 4(m + 1)x
y' = 0 ⇔ 4x(x2 - m - 1) = 0
Hàm số có điểm 3 cực trị 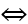m > -1
Khi đó 3 điểm cực trị của đồ thị hàm số là : A(0; m2 ), B(-√(m + 1); -2m -1),C(√(m + 1);-2m - 1)
Do tính chất đối xứng, ta có ΔABC cân tại đỉnh A .
Vậy ΔABC chỉ có thể vuông cân tại đỉnh 
Kết hợp điều kiện ta có: m = 0 ( thỏa mãn).
Lưu ý: Có thể làm theo cách khác:
+) Cách 1: Gọi M là trung điểm của BC, tìm tọa độ điểm M, ΔABC vuông tại đỉnh A thì 2AM = BC.
+) Cách 2: Sử dụng định lý Pitago BC2 = AB2 + AC2
+) Cách 3: 
+) Hoặc sử dụng công thức b3/8a + 1 = 0
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
