Toptailieu.vn xin giới thiệu 50 bài tập trắc nghiệm Cực trị của hàm số (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 12 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán. 

Mời các bạn đón xem:

Cực trị của hàm số

Câu 1: Cho hàm số 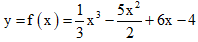 . Tìm mệnh đề đúng?

A. Điểm cực đại của đồ thị hàm số là x = 2.

B. Điểm cực tiểu của đồ thị hàm số là x = 2.

C. Điểm cực đại của đồ thị hàm số là (2; 2/3).

D. Điểm cực tiều của hàm số là (3; 1/2).

Lời giải:

Tập xác định: D = R.

y' = x² - 5x + 6; y' = 0 

y'' = 2x - 5 và y''= 2x - 5

Do y''(2) = - 1 < 0 nên x = 2 là điểm cực đại của hàm số.

Vì y''(3) = 1 > 0 nên x = 3 là điểm cực tiểu của hàm số.

- Suy ra đồ thị hàm số đã cho có một điểm cực đại (2; 2/3), một điểm cực tiểu (3; 1/2)

Đáp án cần chọn là: C

Câu 2: Tìm cực trị của hàm số  .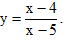

A. x = 5

B. x = 4

C. (4;0)

D. Không có điểm cực trị

Lời giải:

Tập xác định: D = R\{5}.

Suy ra hàm số không có cực trị.

Đáp án cần chọn là: D

Câu 3: Hàm số y= -x³ + 3x² + 1 đạt cực tiểu tại:

A. x = 0

B. x = 2

C. Không có cực tiểu

D. Đáp án khác

Lời giải:

TXĐ: D = R.

Ta có: y' = (-x³ + 3x² + 1)' = -3x² + 6x, y' = 0 ⇔ -3x(x - 2) = 0 

Do y'' = -6x + 6 và y''(0) = 6 > 0 nên x = 0 là điểm cực tiểu của hàm số.

Vì y''(2) = -6 < 0 nên x = 2 là điểm cực đại của hàm số.

Nhận xét: Chúng ta cũng có thể dùng bảng biến thiên để tìm cực đại, cực tiểu của hàm số.

- Bảng biến thiên hàm số: y = -x³ + 3x² + 1

Dựa vào bảng biến thiên ta thấy x = 0 là điểm cực tiểu

Đáp án cần chọn là: A

Câu 4: Khẳng định nào sau đây là sai:

A. 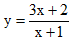 có đạt cực tiểu tại – 1.

B. 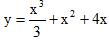 không có cực trị.

C. y = x⁴ + 6x² + 2 đạt cực tiểu là 0.

D. Nếu đạo hàm không đổi dấu trên TXĐ thì hàm không có cực trị.

Lời giải:

Xét phương án

A. 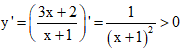 nên hàm số không có cực trị

Suy ra câu A sai.

B. 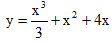 có đạo hàm: y'= x² + 2x + 4 = (x + 1)² + 3 > 0 mọi x nên y là không có cực trị là câu chính xác.

C. y' = 4x³ + 12x = 4x(x² + 3); y' = 0 ⇔ x = 0

y'' = 12x² + 12; y''(0) = 12 > 0

⇒ x = 0 là điểm cực tiểu

D. Đây là câu lí thuyết.

Đáp án cần chọn là: A

Câu 5: Cực trị của hàm số 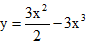 là:

A. x_CD = 0, x_CT = 1/3

B. x_CD = 3, x_CT = -3

C. x_CD = 1/3, x_CT = 0

D. Không có cực trị.

Lời giải:

TXĐP: D = R. Ta có:

y' = 3x - 9x² = 3x(1 - 3x); y' = 0 

y'' = 3 - 18x; y''(0) = 3 > 0; y'(1/3) = -3 < 0

⇒ x_CD = 1/3, x_CT = 0

Kết luận: hàm số đạt cực trị với x_CD = 1/3, x_CT = 0

Đáp án cần chọn là: C

Câu 6: Hàm số y = ax⁴ + bx² + c với a ≠ 0 có tối đa bao nhiêu cực trị?

A. 1

B. 2

C. 3

D. 4

Lời giải:

Đạo hàm: y' = 4ax³ + 2bx là hàm bậc ba.

Phương trình bậc 3: y' = 0 có tối đa 3 nghiệm. Vậy số điểm cực trị tối đa là 3.

Đáp án cần chọn là: C

Câu 7: Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau:

Khẳng định nào sau đây là khẳng định đúng ?

A. Hàm số có đúng một cực trị.

B. Hàm số có giá trị cực tiểu bằng 1.

C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1.

D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1.

Lời giải:

Do hàm số xác định tại x = 0 và đạo hàm đổi dấu từ dương sang âm khi x qua x = 0 nên hàm số đạt cực đại tại x = 0 .

Do hàm số xác định tại x = 1; y'(1) = 0 và đạo hàm đổi dấu từ âm sang dương khi x qua x = 1 nên hàm số đạt cực tiểu tại x = 1 .

Đáp án cần chọn là: D

Câu 8: Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau:

Khẳng định nào sau đây là khẳng định đúng ?

A. Hàm số có đúng một cực trị.

B. Hàm số có giá trị cực tiểu bằng 1.

C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1.

D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1.

Lời giải:

Do hàm số xác định tại x = 1, y'(1) = 0 và đạo hàm đổi dấu từ âm sang dương khi x đi qua x = 1 nên hàm số đạt cực tiểu tại x = 1; giá trị cực tiểu là y(1) = -1.

  + Tại x = 0 hàm số không xác định nên x= 0 không là điểm cực trị củ hàm số.

  + Hàm số không có giá trị lớn nhất; giá trị nhỏ nhất.

Đáp án cần chọn là: A

Câu 9: Cho hàm số y = f(x) liên tục tại x₀ và có bảng biến thiên

Khi đó hàm số đã cho có:

A. Hai điểm cực đại, một điểm cực tiểu.

B. Một điểm cực đại, không có điểm cực tiểu.

C. Một điểm cực đại, hai điểm cực tiểu.

D. Một điểm cực đại, một điểm cực tiểu.

Lời giải:

Hàm số không có đạo hàm tại x₀ nhưng hàm số vẫn liên tục tại x₀ thì hàm số vẫn đạt cực trị tại x0.

Trong trường hợp này; hàm số đạt cực đại tại điểm x₁ và đạt cực tiểu tại x₀.

Do đó đáp án D đúng.

Đáp án cần chọn là: D

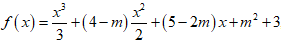
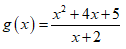
Câu 10: Cho hàm số  với m là tham số thực. Hàm số  có đồ thị (C) và bảng biến thiên sau:

Tìm m sao cho hàm số f(x) đạt cực trị ít nhất tại một điểm mà điểm đó lớn hơn -1?

A. m > 2

B. 

C. m < -5/2

D. m > 5/2

Lời giải:

Ta có: f'(x)= x² + (4 - m)x + 5 - 2m

Xét phương trình: f'(x) = x² + (4 - m)x + 5 – 2m = 0

⇒ x² + 4x + 5 = m(x + 2) 

Ta có nghiệm của f'(x) = 0 cũng là hoành độ giao điểm của phương trình g(x) = m

Khi đó từ bảng biến thiên, để hàm số đạt cực trị tại ít nhất tại 1 điểm mà điểm đó lớn hơn – 1 khi và chỉ khi m > 2.

Đáp án cần chọn là: A

Câu 11: Cho hàm số y = f(x) có f'(x) = x(x-1)².(x + 1)³, hỏi số điểm cực trị của hàm số y = f(x).

A. 1

B. 2

C. 3

D. 4

Lời giải:

f'(x) = 0 ⇔ x(x-1)².(x + 1)³ = 0 

Do x = 1 là nghiệm kép nên không là điểm cực trị của hàm số.

Do x = 0 là nghiệm đơn nên là điểm cực trị của hàm số.

Do x = -1 là nghiệm bội lẻ nên là điểm cực trị của hàm số.

Vậy hàm số đã cho có 2 điểm cực trị.

Đáp án cần chọn là: B

Câu 12: Hàm số f(x) có đạo hàm f'(x) trên khoảng K. Cho đồ thị của hàm số f'(x) trên khoảng K như sau:

Số điểm cực trị của hàm số f(x) trên K là:

A. 1

B. 2

C. 3

D. 4

Lời giải:

Dựa vào đồ thị ta thấy phương trình f'(x) = 0 chỉ có một nghiệm đơn (tại x = -1) và hai nghiệm kép (tại x = 0 và x = 2).

Suy ra f'(x) chỉ đổi dấu khi qua nghiệm đơn này. Do đó, hàm số f(x) có đúng một cực trị.

Đáp án cần chọn là: A

Câu 13: Hàm số f(x) có đạo hàm f'(x) trên khoảng K. Cho đồ thị của hàm số f'(x) trên khoảng K như sau:

Số điểm cực trị của hàm số y= f(x) + 2018 trên K là:

A. 1

B. 2

C. 3

D. 4

Lời giải:

Dựa vào đồ thị ta thấy phương trình f'(x) = 0 có ba nghiệm đơn (đồ thị hàm số y = f'(x) = 0 cắt trục hoành tại 3 điểm phân biệt) nên y' đổi dấu khi qua nghiệm đơn này.

Lại có: y = f(x) + 2018 có y'= f'(x). Do đó suy ra hàm số y= f(x) + 2018 có ba điểm cực trị.

Đáp án cần chọn là: C

Câu 14: Hàm số f(x) có đạo hàm f'(x) trên khoảng K. Cho đồ thị của hàm số f'(x) trên khoảng K như sau:

Số điểm cực trị của hàm số y= f(x) + 2x trên K là:

A. 0

B. 1

C. 2

D. 3

Lời giải:

Hàm số y= f(x) + 2x có đạo hàm y'= f'(x) + 2

Phương trình y’= 0 ⇔ f'(x) = -2

Số nghiệm của phương trình y' = 0 là số giao điểm của đồ thị hàm số y = f'(x) và đường thẳng y = - 2

Dựa vào đồ thị ta thấy phương trình y'= 0 có hai nghiệm và y' không đổi dấu khi qua các nghiệm này. Do đó suy ra hàm số y = f(x) + 2x không có cực trị.

Đáp án cần chọn là: A

Câu 15: Hàm số f(x) có đạo hàm f’(x) trên R. Cho đồ thị của hàm số f’(x) như sau:

Số điểm cực trị của hàm số y = f(x²) là:

A. 1

B. 2

C. 3

D. 4

Lời giải:

Ta có: y = f(x²) nên y'= 2x. f'(x²)

Dấu y':

Do đó suy ra hàm số y= f(x²) có ba điểm cực trị.

Đáp án cần chọn là: C

Câu 16: Hàm số y = f(x) có đồ thị như hình bên dưới. Hỏi đồ thị hàm số có mấy điểm cực trị:

A. 3.

B. 2.

C. 1.

D. 0.

Lời giải:

Căn cứ vào sự đi lên đi xuống của đồ thị ta thấy hàm số có 3 điểm cực trị.

Đáp án cần chọn là: A

Câu 17: Cho hàm số y = f(x) có đạo hàm và liên tục trên R, hàm số y = f(x) đồ thị như hình vẽ:

Số điểm cực trị của hàm số y = |f(x)| là:

A. 3

B. 4

C. 7

D. 0

Lời giải:

Từ đồ thị hàm số y = f(x) ta suy ra đồ thị hàm số y = |f(x) |.

Dựa vào đồ thị hàm số suy ra hàm số y = |f(x)| có 7 điểm cực trị.

Đáp án cần chọn là: C

Câu 18: Cho hàm số y = f(x) có đạo hàm và liên tục trên R, hàm số y = f(x) đồ thị như hình vẽ sau. Số điểm cực trị của hàm số y = f(|x|) là:

A. 0

B. 2

C. 4

D. 5

Lời giải:

Từ đồ thị hàm số y = f(x) ta suy ra đồ thị hàm số y = f(|x|).

Từ đồ thị hàm số y= f(|x|); suy ra hàm số có 5 điểm cực trị.

Đáp án cần chọn là: D

Câu 19: Cho hàm số y = f(x) có đạo hàm và liên tục trên R, hàm số y = f(x) có đồ thị như hình vẽ sau. Số điểm cực trị của hàm số y = |2f(x) – 3| là:

A. 3

B. 5

C. 7

D. 9

Lời giải:

Từ đồ thị hàm số y= f(x) ta suy ra đồ thị hàm số y = |2f(x) - 3|

Suy ra đồ thị hàm số y = |2f(x) - 3| có 7 điểm cực trị.

Đáp án cần chọn là: C

Câu 20: Cho hàm số y = f(x) có đạo hàm và liên tục trên R, hàm số y = f(x) đồ thị như hình vẽ:

Số điểm cực trị của hàm số y = |[f(x)]² - 1| là:

A. 7

B. 9

C. 11

D. 13

Lời giải:

Đặt u(x) = f²(x) – 1

Đạo hàm: u'(x) = 2f(x).f'(x)

Phương trình u'(x) = 0 có các nghiệm đơn.

Suy ra đồ thị hàm số y = |[f(x)]² - 1|

Đồ thị hàm số y = |[f(x)]² - 1| có 13 điểm cực trị.

Đáp án cần chọn là: D

Câu 21: Hàm số 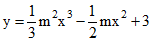 với m ≠ 0 đạt cực đại tại x = -4/5 với giá trị của m nào dưới đây ?

A. m = 0

B. m = -13/5

C. m = -5/4

D. m = 2/3

Lời giải:

Hàm số đạt giá trị cực đại tại x khi y'(x) = 0 và y''(x) < 0

Ta có: y'(x) = m².x² – 2mx và y'' = 2m²x – 2m

- Hàm số đạt cực đại tại x = -4/5 khi

Đáp án cần chọn là: C

Câu 22: Tìm giá trị cực đại y_CĐ của hàm số y = x³ – 3x + 2

A. y_CĐ = 4

B. y_CĐ = 1

C. y_CĐ = 0

D. y_CĐ = -1

Lời giải:

Đạo hàm: y'= 3x² – 3

Xét phương trình y' = 0 ⇔ 3x² – 3 = 0 ⇔ x = 1 hoặc x = -1.

Ta có y'' = 6x.

Do y''(1)= 6 > 0 nên điểm x = 1 là điểm cực tiểu của hàm số.

Do y''(-1)= -6 < 0 nên điểm x = -1 là điểm cực đại của hàm số

⇒ Giá trị cực đại là: y_CĐ = y(-1) = 4.

Đáp án cần chọn là: A

Câu 23: Cho hàm số 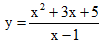 có 2 cực trị x₁, x₂. Tính S = x₁ + x₂.

A. S = 2

B. S = -2

C. S = 2√3

D. S = -2√3

Lời giải:

TXĐ: D = R\{1}

 

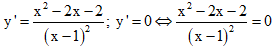
Vậy S = x₁ + x₂ = 2.

Đáp án cần chọn là: A

Câu 24: Tìm m để hàm số 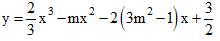 có 2 cực trị x₁, x₂ thỏa mãn x₁.x₂ + 2.(x₁ + x₂) = 1

A. m = 2/√3

B. m = 3/√2

C. m = 2/3

D. Đáp án khác

Lời giải:

Đạo hàm: y' = 2x² – 2mx – 2(3m² - 1)

Xét phương trình y' = 0 ⇔ x² – mx – 3m² + 1 = 0

Để hàm số có 2 điểm cực trị

⇔ Δ = b² - 4ac = 13m² - 4 > 0 

Khi đó: x₁.x₂ + 2(x₁ + x₂) = 1 ⇔ -3m² + 1 + 2m = 1 

Vậy m = 2/3 thỏa điều kiện đặt ra.

Đáp án cần chọn là: C

Câu 25: Cho hàm số y= -x⁴ + (5m - 1)x² + 2. Hàm số đã cho có đúng 1 cực trị với giá trị nào của m sau đây ?

A. m ≥ 1/5 

B. m > 1/5

C. m < 1/5 

D. m ≤ 1/5

Lời giải:

y' = -4x³ + 2(5m - 1)x; y' = 0 

Để hàm số có đúng 1 cực trị 

Đáp án cần chọn là: D

Câu 26: 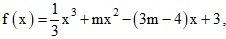 , với giá trị nào của m thì hàm số có cực tiểu, cực đại

A. 4 ≤ m ≤ 1

B. -4 ≤ m ≤ 1

C. m < -4 hoặc m > 1 

D. m ≤ -4 hoặc m ≥ 1

Lời giải:

Đạo hàm: f'(x) = x² + 2mx – 3m + 4

Xét phương trình: f'(x) = 0 hay x² + 2mx – 3m + 4 =0

Hàm số đã cho có cực đại và cực tiểu khi và chỉ khi f'(x) = 0 có 2 nghiệm phân biệt.

Δ' = m² + 3m - 4 > 0 

Đáp án cần chọn là: C

Câu 27: Hàm số y = ax³ + bx² + cx + d với a ≠ 0 có 2 cực trị khi nào ?

A. y' = 0 có nghiệm.

B. y' = 0 có 2 nghiệm phân biệt.

C. y' = 0 có 2 nghiệm trái dấu.

D. Hàm số luôn có 2 cực trị.

Lời giải:

Hàm số bậc ba y = ax³ + bx² + cx + d với a ≠ 0 có đạo hàm y' = 3ax² + 2bx + c (*)

Để hàm số đã cho có hai điểm cực trị khi và chỉ khi y' = 0 có 2 nghiệm phân biệt.

Đáp án cần chọn là: B

Câu 28: Cho hàm số 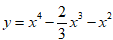 . Mệnh đề nào sau đây là đúng?

A. Hàm số có giá trị cực tiểu là 0.

B. Hàm số có hai giá trị cực tiểu là -2/3 và -5/48.

C. Hàm số chỉ có một giá trị cực tiểu.

D. Hàm số có giá trị cực tiểu là -2/3 và giá trị cực đại là -5/48.

Lời giải:

TXĐ: D = R và có đạo hàm y' = 4x³ – 2x² – 2x = 2x(2x² – x – 1)

Bảng biến thiên

Dựa vào bảng biến thiên ta có đáp án B.

Đáp án cần chọn là: B

Câu 29: Tọa độ điểm cực đại của hàm số y = x³ – 3x² + 4 là:

A. (2;4)

B. (2; 0)

C. (0;- 4)

D. (0 ; 4)

Lời giải:

Tập xác định: D= R.

Đạo hàm y’= 3x2 – 6x

Xét phương trình: y' = 0 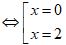 ; y'' = 6x - 6

Ta có: y''(0) = - 6 < 0 nên điểm cực đại của hàm số là x = 0 và y_CĐ = 4.

Do y''( 2) = 6 > 0 nên điểm x = 2 là điểm cực tiểu của hàm số và y_CT = 0 .

Vậy điểm cực đại của đồ thị hàm số là (0; 4)

Đáp án cần chọn là: D

Câu 30: Cho hàm số y = x³ – 3x² +1 (C). Đường thẳng đi qua điểm A(- 1; 1) và vuông góc với đường thẳng đi qua hai điểm cực trị của (C) có phương trình là

A. y = - x

B. x - 4y + 5 = 0

C. y = 2x + 3

D. x - 2y + 3 = 0

Lời giải:

Cách 1: TXĐ: D = R.

Đạo hàm y'= 3x² – 6x

Ta có: y = 1/3. (x + 1).y' + (-2x + 1).

Suy ra; đường thẳng đi qua 2 điểm cực trị là Δ: y = -2x + 1

Đường thẳng d vuông góc Δ có dạng d: y = 1/2.x + b

Do A(-1;1) ∈ d ⇒ 1 = -1/2 + b ⇒ b = 3/2.

Vậy đường thẳng d cần tìm là y = 1/2.x + 3/2 hay d: x – 2y + 3 = 0

Cách 2: Ta có: y'= 3x² - 6x

Tọa độ hai điểm cực trị: B(0; 1) và C(2; -3)

Hệ số góc của đường thẳng BC là: 

⇒ Hệ số góc của đường thẳng cần tìm k_d = 1/2

(Vì đường thẳng cần tìm vuông góc với đường thẳng tạo bởi hai điểm cực trị nên k_BC. k_d = -1)

Phương trình đường thẳng d: y = 1/2.(x + 1) + 1 ⇔ x – 2y + 3 = 0.

Đáp án cần chọn là: D

Câu 31: Cho hàm số y = x³ – 3x có giá trị cực đại và cực tiểu lần lượt là y₁; y₂. Khi đó:

A. y₁ + y₂ = 1

B. 2y₁ – y₂ = 4

C. 2y₂ + y₁ = 2

D. y₁ - y₂ = 4

Lời giải:

Ta có: y' = 3x² - 3 = 0 

Do y'' = 6x; y''(1) = 6 > 0 nên điểm x = 1 là điểm cực tiểu của hàm số

Vì y''(-1)= -6 < 0 nên điểm x = -1 là điểm cực đại của hàm số.

Suy ra y₁ = y(-1) = 2; y₂ = y(1) = -2

Vậy y₁ – y₂ = 4.

Đáp án cần chọn là: D

Câu 32: Đồ thị của hàm số y = 3x⁴ – 4x³ – 6x² + 12x + 1 đạt cực tiểu tại M(x₁; y₁). Tính tổng S = x₁ + y₁

A. 5

B. - 11

C. 7   

D. 6

Lời giải:

Đạo hàm y' = 12x³ – 12x² – 12x + 12

y' = 0 ⇔ x³ - x² - x + 1 = 0 ⇔ (x + 1)(x - 1)² = 0 

Lập bảng biến thiên, ta thu được điểm cực tiểu là M(-1; -10)

Do đó tổng S = x₁ + y₁ = -11

Đáp án cần chọn là: B

Câu 33: Cho hàm số y = f(x) liên tục trên đoạn [0; 4] có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?

A. Hàm số đạt cực đại tại x = 4.

B. Hàm số đạt cực tiểu tại x = 1.

C. Hàm số đạt cực đại tại x = 2.

D. Hàm số đạt cực tiểu tại x = 3.

Lời giải:

Dựa vào đồ thị hàm số như hình vẽ thì hàm số đạt cực tiểu tại x = 3 và đạt cực đại tại x = 1.

Đáp án cần chọn là: D

Câu 34: Cho hàm số 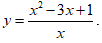 Tính tổng giá trị cực đại y_CĐ và giá trị cực tiểu y_CT của hàm số trên.

A. –5

B. 2

C. –4

D. -6

Lời giải:

Tập xác định: D = R\{0}.

Có 

Suy ra: y_CĐ + y_CT = -1 + (-5) = -6 .

Đáp án cần chọn là: D

Câu 35: Cho hàm số y = (x - 1).(x + 2)². Trung điểm I của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số nằm trên đường thẳng nào dưới đây?

A. 2x + y + 4 = 0   

B. 2x + y - 2 = 0

C. x + 2y + 1 = 0

D. x + y + 1 = 0

Lời giải:

Ta có: y = (x - 1).(x + 2)² = x³ + 3x² - 4

Đạo hàm: y' = 3x² + 6x và y'' = 6x + 6.

Đối với hàm bậc ba, trung điểm của hai điểm cực trị của đồ thị hàm số chính là điểm uốn của đồ thị. Do đó, trung điểm I cần tìm có hoành độ x_I thỏa mãn: 6x_I + 6 = 0 ⇔ x_I = - 1.

⇒ y_I = -2

Vậy điểm I cần tìm là (-1; -2). Dễ thấy điểm I thuộc đường thẳng 2x + y + 4 = 0

Đáp án cần chọn là: A

Câu 36: Cho hàm số 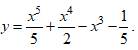 Mệnh đề nào sau đây là đúng?

A. Hàm số đạt cực đại tại x = -3; đạt cực tiểu tại x = 1.

B. Hàm số đạt cực tiểu tại x = -3; đạt cực đại tại x = 1.

C. Hàm số đạt cực tiểu tại x = -3 và x = 1; đạt cực đại tại x = 0.

D. Hàm số đạt cực đại tại x = -3 và x = 1; đạt cực tiểu tại x = 0.

Lời giải:

Đạo hàm: y' = x⁴ + 2x³ – 3x² = x²(x² + 2x – 3)

Bảng biến thiên

Dựa vào bảng biến thiên suy ra hàm số đạt cực tiểu tại x = 1 và đạt cực đại tại x = -3.

Đáp án cần chọn là: A

Câu 37: Biết đồ thị hàm số y = ax³ + bx² + cx + d có hai điểm cực trị là (-1; 18) và (3; -16). Tính a + b + c + d ?

A. – 2

B. -1

C. 1 

D. 2

Lời giải:

Đạo hàm: y' = 3ax² + 2bx + c

Xét phương trình: y’ = 0 ⇔ 3ax² + 2bx + c = 0 (*)

Do đồ thị hàm số có 2 điểm cực trị nên (*) có 2 nghiệm phân biệt.

Theo hệ thức Vi- et ta có:

Mà 2 điểm cực trị là (-1; 18) và (3; -16) thuộc đồ thị hàm số nên ta có:

-a + b – c + d = 18 (3) và 27a + 9b + 3c + d = -16 ( 4).

Giải hệ 4 phương trình (1); (2); (3); (4) ta có:

Suy ra a + b + c + d = 1.

Đáp án cần chọn là: C

Câu 38: Cho hàm số y= -x³ + (m + 1)x² – (m² + 2m - 3)x – 4, xác định tham số m để đồ thị hàm số y có 2 điểm cực trị nằm về 2 phía của trục trung:

A. m > 3

B. -3 < m < 1

C. -3 ≤ m ≤ 1 

D. Với mọi giá trị m.

Lời giải:

Đạo hàm: y' = -3x² + 2(m + 1)x – (m² + 2m - 3) (*)

Để đồ thị hàm có hai điểm cực trị nằm về hai phía so với trục tung khi và chỉ khi (*) có hai nghiệm trái dấu:

Đáp án cần chọn là: B

Câu 39: Giá trị cực tiểu của y = x + 1/x là giá trị nào sau đây ?

A. - 1

B. 1

C. -2

D. 2

Lời giải:

Cách 1: Dùng bảng biến thiên.

Cách 2: Dùng y''

 suy ra hàm số đạt cực tiểu tại x = 1.

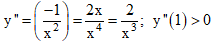
Vậy giá trị cực tiểu là y(1) = 2.

Đáp án cần chọn là: D

Câu 40: Tìm điều kiện của m để hàm số y = 2x⁴ – 4(m + 5)x² + m² – 4 có 3 cực trị:

A. m ∈ (-∞; -5)

B. m ∈ (-∞; -5]

C. m ∈ [5; +∞)

D. m ∈ (5; +∞)

Lời giải:

Đạo hàm: y' = 8x³ – 8(m + 5)x

Xét phương trình y' = 0 ⇔ 8x[x² – (m + 5)] = 0

Để hàm số đã cho có 3 điểm cực trị khi và chỉ khi phương trình (*) có hai nghiệm phân biệt khác 0

⇔ m + 5 > 0 hay m > -5.

Đáp án cần chọn là:

Câu 41: Cho hàm số y = f(x) = ax³ + bx² + cx + d. Hàm số có cực trị là (0; 1); (1; -1). Khi đó xác định hàm số f(x)?

A. f(x) = x³ + 3x + 1

B. f(x) = x³ - 3x + 1

C. f(x) = -x³ + 3x

D. f(x) = 2x³ + 6x + 1

Lời giải:

Đạo hàm: y' = 3ax² + 2bx + c

Hàm số có 2 cực trị là (0; 1) và (1; -1) nên ta có hệ phương trình:

Vậy hàm số cần tìm là: y = x³ – 3x² + 1

Đáp án cần chọn là: B

Câu 42: Giả sử m là số cực trị của hàm y = ax³ + bx² + 1 (a ≠ 0). Xét trên khoảng (1; +∞), m có thể bằng bao nhiêu?

A. m = 1

B. m = 1 hoặc m = 2

C. m = 0 hoặc m = 2

D. m = 1 hoặc m = 0

Lời giải:

Ta sẽ tính đạo hàm và tìm cực trị của hàm số sau đó xét các cực trị thuộc khoảng (1; +∞)

Đạo hàm: y'= 3ax² + 2bx = x.(3ax + 2b)

Rõ ràng điểm 0 ∉ (1; +∞) còn -2a/3a có thể ∈ (1; +∞).

Vậy hàm số đã cho có thể có 0 hoặc 1 cực trị trên khoảng (1; +∞).

Đáp án cần chọn là: D

Câu 43: Hàm số y = ax³ + ax² - 4 đạt cực tiểu tại x = -2/3 thì a thỏa mãn điều kiện gì ?

A. a > 0

B. a < 0

C. a = 0

D. a ≠ 0

Lời giải:

Đạo hàm y' = 3ax² + 2ax (*)

- Để hàm số có cực đại cực tiểu khi và chỉ khi (*) có hai nghiệm phân biệt:

⇔ Δ' > 0 ⇔ a ≠ 0 (1)

- Hàm số có cực trị tại x = -2/3 nên:

- Kết hợp (1), (2) suy ra a ≠ 0

Đáp án cần chọn là: D

Câu 44: Cho hàm trùng phương y = -2x⁴ + 4(2m² + 1)x² + 1, giá trị nhỏ nhất của y_CĐ là bao nhiêu

A. min = 1

B. min = 3

C. min = 0

D. min = 2

Lời giải:

Đạo hàm: y' = -8x³ + 8(2m² + 1)x = -8x.[x² – (2m² + 1)].

Nhận xét: Hàm trùng phương có 3 cực trị với hệ số a < 0 sẽ có 2 cực đại và 1 cực tiểu. Từ đó ta xác định được giá trị cực đại:

y_CD = -2(2m² + 1)² + 4(2m² + 1)² = 2(2m² + 1)² + 1

Vì 2m² + 1 ≥ 1 nên 2(2m² + 1)² + 1 ≥ 2 + 1 = 3

Do đó min y_CĐ = 3. Dấu "=" xảy ra khi m = 0

Đáp án cần chọn là: D

Câu 45: Định m để 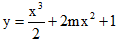 đạt cực tiểu tại x = -1

A. m = 1/4

B. m = 1/2

C. m = 1

D. Không có giá trị nào thỏa mãn

Lời giải:

Đạo hàm: y'= x² + 4mx và y'' = 2x + 4m

Để hàm đạt cực tiểu tại x = -1

Vậy không có giá trị nào của m thỏa mãn.

Đáp án cần chọn là: D

Câu 46: Cho hàm số:

Xác định giá trị m để cực đại và cực tiểu nằm trong khoảng (-3;4)

A. m ∈ (-2; 5)

B. m ∈ (-2; 5)\{3}

C. m ∈ (-∞; 2)

D. m ∈ (3; 5)

Lời giải:

Ta cần tìm cực đại và cực tiểu; sau đó cho thuộc vào khoảng đề bài yêu cầu.

Đạo hàm: y’ = x2 + (m- 1)x + m - 2

Để hàm có cực đại, cực tiểu khi và chỉ khi:

Δ = (m - 1)² - 4.1.(m - 2) > 0 ⇔ (m - 3)² > 0 ⇔ m ≠ 3 (1)

Với điều kiện trên phương trình y’ = 0 có 2 nghiệm là:

Vì x₁ đã thuộc (-3; 4) nên ta chỉ cần định điều kiện để x₂ thuộc (-3; 4).

Để x₂ thuộc (-3;4) ⇔ -3 < 2 - m < 4 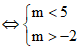 kết hợp (1) ta được m ∈ (-2; 5)\{3}

Đáp án cần chọn là: B

Câu 47: Đồ thị hàm số 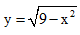 có mấy điểm cực tiểu ?

A. 0

B. 1

C. 2

D. 3

Lời giải:

TXĐ: D = [-3; 3]

Bảng biến thiên

Dựa vào bảng biến thiên ta suy ra hàm số không có cực tiểu

Đáp án cần chọn là: A

Câu 48: Đường thẳng y = x³ + 3x² – 3x + 1 có 2 điểm cực trị A và B. Đường thẳng song song với AB có thể là đường nào trong các đường thẳng dưới đây

A. 4x + y – 2 = 0

B. y = -4x + 3

C. 4x + 2y + 3 = 0

D. y = 1/4.x - 2

Lời giải:

Tính đạo hàm, thực hiện phép chia y/y' ta được:

Vậy đường thẳng qua 2 điểm cực trị là: y = -4x + 2

Ta thấy đường thẳng đi qua hai điểm cực trị song song với đường thẳng y = -4x + 3.

Đáp án cần chọn là: B

Câu 49:Hàm số 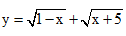 tìm mệnh đề đúng?

A. Giá trị cực tiểu là 2√3

B. Giá trị cực đại là 2√3

C. Điểm cực tiểu có hoành độ là –2

D. Điểm cực đại có hoành độ là 2

Lời giải:

TXĐ: D= [-5; 1]

Xét phương trình y’= 0 

- Bảng biến thiên

Dựa vào bảng biến thiên hàm số đạt cực đại tại x = -2 và giá trị cực đại là 2√3

Đáp án cần chọn là: B

Câu 50: Hàm số y = x³ + mx + 201 có cả cực đại và cực tiểu khi.

A. m < 0

B. m > 0

C. m ≥ 0 

D. m ≤ 0

Lời giải:

Đạo hàm y = 3x² + m

Hàm số y = x³ + mx + 201 có cả cực đại và cực tiểu khi và chỉ khi phương trình y’ = 0 có hai nghiệm phân biệt.

Vậy m < 0.

Đáp án cần chọn là: A