Toptailieu.vn xin giới thiệu 50 bài tập trắc nghiệm Sự đồng biến, nghịch biến của hàm số (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 12 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
Sự đồng biến, nghịch biến của hàm số
Câu 1: Cho hàm số y = sin2x - 2x. Hàm số này
A. Luôn đồng biến trên R
B. Chỉ đồng biến trên khoảng (0; +∞)
C. Chỉ nghịch biến trên (-∞; -1)
D. Luôn nghịch biến trên R
Lời giải:
Tập xác định D = R
Ta có : y' = 2.cos2x - 2 = 2(cos2x - 1) ≤ 0; ∀ x
(vì -1 ≤ cos2x ≤ 1)
Vậy hàm số luôn nghịch biến trên R
Đáp án cần chọn là: D
Câu 2: Tìm m để hàm số
luôn nghịch biến trên khoảng xác định.
A.-2 < m ≤ 2
B. m < -2 hoặc m > 2
C. -2 < m < 2
D. m ≠ ±2
Lời giải:
Tập xác định
Hàm số nghịch biến trên từng khoảng
khi và chỉ khi
Suy ra m2 - 4 < 0 hay -2 < m < 2.
Đáp án cần chọn là: C
Câu 3: Cho hàm số y = -x3 + 3x2 + 3mx - 1, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)
A. m < 1
B. m ≥ 1
C. m ≤ -1
D. m ≥ -1
Lời giải:
Ta có y' = -3x2 + 6x + 3m. Hàm số nghịch biến trên khoảng (0; +∞) nếu y' ≤ 0 trên khoảng (o; +∞)
Cách 1: Dùng định lí dấu tam thức bậc hai.
Xét phương trình -3x2 + 6x + 3m. Ta có Δ' = 9(1 + m)
TH1: Δ' ≤ 0 => m ≤ -1 khi đó, -3x2 + 6x + 3m < 0 nên hàm số nghịch biến trên R .
TH2: Δ' > 0 => m > -1; y' = 0 có hai nghiệm phân biệt là x = 1 ±√(1+m) .
Hàm số nghịch biến trên (0; +∞) <=> 1 + √(1+m) ≤ 0, vô lí.
Từ TH1 và TH2, ta có m ≤ -1
Cách 2: Dùng phương pháp biến thiên hàm số.
Ta có y' = -3x2 + 6x + 3m ≤ 0, ∀x > 0 <=> 3m ≤ 3x2 - 6x, ∀x > 0
Từ đó suy ra 3m ≤ min(3x2 - 6x) với x > 0
Mà 3x2 -6x = 3(x2 -2x + 1) - 3 = 3(x - 1)2 - 3 ≥ -3 ∀ x
Suy ra: min( 3x2 – 6x) = - 3 khi x= 1
Do đó 3m ≤ -3 hay m ≤ -1.
Đáp án cần chọn là: C
Câu 4: Cho đồ thị hàm số y = -x3 như hình vẽ. Hàm số y = -x3 nghịch biến trên khoảng:
A. (-1;0)
B. (-∞;0)
C. (0;+∞)
D. (-1;1)
Lời giải:
Trên khoảng (0; +∞) đồ thị hàm số đi xuống từ trái sang phải.
Do đó hàm số nghịch biến trên khoảng (0;+∞)
Đáp án cần chọn là: C
Câu 5: Cho đồ thị hàm số y = -2/x như hình vẽ. Hàm số y = -2/x đồng biến trên
A. (-∞;0)
B. (-∞;0) ∪ (0;+∞)
C. R
D. (-∞;0) và (0;+∞)
Lời giải:
Đồ thị hàm số đi lên từ trái sang phải trên hai khoảng (-∞;0) và (0;+∞)
Ghi chú. Những sai lầm có thể gặp trong quá trình làm bài:
- Không chú ý tập xác định nên chọn đáp án C.
- Không chú ý định nghĩa của hàm đồng biến nên chọn đáp án B.
Đáp án cần chọn là: D
Câu 6: Cho hàm số f(x) có đạo hàm f'(x) = √x(x-1)(x+2)2
Kết luận nào sau đây là đúng?
A. Hàm số f(x) nghịch biến trên khoảng (-∞;1).
B. Hàm số f(x) đồng biến trên các khoảng (-∞;0) và (1;+∞).
C. Hàm số f(x) đồng biến trên các khoảng và (1;+∞).
D. Hàm số f(x) đồng biến trên các khoảng (1;+∞).
Lời giải:
Điều kiện: x > 0
Bảng xét dấu :
Vậy f(x) đồng biến trên khoảng (1;+∞) và nghịch biến trên khoảng (0;1).
Đáp án cần chọn là: D
Câu 7: Khoảng nghịch biến của hàm số y = x3/3 - 2x2 + 3x + 5 là:
A. (1;3)
B.(-∞; 1) ∪ (3; +∞)
C. (-∞; 1) và (3; +∞)
D. (1;+∞)
Lời giải:
Bảng xét dấu y’ :
Vậy hàm số nghịch biến trên khoảng (1;3).
Đáp án cần chọn là: A
Câu 8: Cho hàm số y = x4 - 2x2 + 3 . Kết luận nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng (-∞; -1) ∩ (0; 1)
B. Hàm số đồng biến trên khoảng (-1; 0) ∪ (1; +∞)
C. Hàm số nghịch biến trên khoảng (-∞; -1) ∪ (0; 1)
D. Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞)
Lời giải:
Bảng xét dấu y’:
Từ đó ta có: Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞), nghịch biến trên các khoảng (-∞; -1) và (0; 1).
Đáp án cần chọn là: D
Câu 9: Cho hàm số y = x3 - x2 + (m-1)x + m. Tìm điều kiện của tham số m để hàm số đồng biến trên R
A. m ≤ 2
B. m > 2
C. m ≥ 2
D. m <2
Lời giải:
y' = x2 - 2x + (m -1).
Hàm số đồng biến trên R ⇔ y' ≥ 0 ∀x ∈ R
⇒ Δ = (-1)2 - (m-1) = -m + 2 ≤ 0 ⇔ m > 2
Đáp án cần chọn là: B
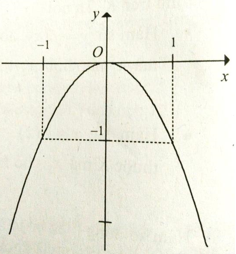
Câu 10: Cho hàm số
Tìm giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1).
A. m < 2√2
B. m ≥ -2√2
C. m = 2√2
D. -2√2 ≤ m 2√2
Lời giải:
Ta có y' = -x2 - mx - 2 . Hàm số nghịch biến trên khoảng (-∞; - 1) nếu y' = x2 - mx - 2 ≤ 0 trên khoảng (-∞; -1)
Cách 1. Dùng định lí dấu của tam thức bậc hai. Ta có Δ = m2 - 8
TH1: -2√2 ≤ m ≤ 2√2 => Δ ≤ 0.
Lại có, hệ số a= -1 < 0 nên y' ≤ 0 ∀ x
Hàm số nghịch biến trên R
TH2: 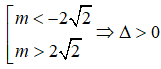
Từ TH1 và TH2, ta có m ≤ 2√2
Cách 2. Dùng phương pháp biến thiên hàm số
Ta có
Từ đó suy ra
Do đó m ≤ 2√2
Vậy giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1) là m = 2√2
Đáp án cần chọn là: C
Câu 11: Tìm tất cả các giá trị của tham số m sao cho hàm số
A. 1 < m < 5
B. m ≥ 5
C. m < -1 hoặc m > 5
D. m > 5
Lời giải:
Đáp án cần chọn là: D
Câu 12: Cho hàm số y = x3 + 3x2 + mx + 1 - 2m. Tìm các giá trị của m để hàm số đồng biến trên đoạn có độ dài bằng 1.
A. m =0
B. m = 1/4
C. 9/4
D. Không tồn tại
Lời giải:
y' = 3x2 + 6x + m. Hàm số đồng biến nếu y' ≥ 0. Ta có Δ' = 9 - 3m
TH1: m ≥ 3 => Δ' ≤ 0 .
Hàm số đồng biến trên R. Do đó m ≥ 3 không thỏa mãn yêu cầu đề bài
TH2: m < 3 => Δ' > 0 .
y’ có hai nghiệm phân biệt là
Từ bảng biến thiên, ta thấy không tồn tại m để hàm số đồng biến trên đoạn có độ dài bằng 1.
Từ TH1 và TH2, không tồn tại m thỏa mãn.
Đáp án cần chọn là: D
Câu 13: Cho đồ thị hàm số có dạng như hình vẽ.
Hàm số đồng biến trên:
A. (0;1)
B. (1;3)
C. (0; 1) ∪ (1; 3)
D. (0;1) và (1;3).
Lời giải:
Trên khoảng (0; 1) đồ thị hàm số đi lên từ trái qua phải
Trên khoảng (1; 3) đồ thị hàm số đi lên từ trái qua phải
Đồ thị hàm số bị gián đoạn tại x = 1. Do đó hàm số đồng biến trên từng khoảng (0; 1) và (1; 3)
Đáp án cần chọn là: D
Câu 14: Tìm khoảng đồng biến của hàm số y = 2x3 - 9x2 + 12x + 3
A.(-∞; 1) ∪ (2; +∞)
B. (-∞ 1] và [2; +∞)
C. (-∞; 1) và (2; +∞)
D. (1;2)
Lời giải:
Ta có
Bảng xét dấu đạo hàm:
Hàm số đồng biến trên các khoảng (-∞; 1) và (2; +∞)
Đáp án cần chọn là: B
Câu 15: Khoảng nghịch biến của hàm số y = x4 - 2x2 - 1 là:
A. (-∞; -1) và (0; 1)
B. (-∞; 0) và (1; +∞)
C. (-∞; -1) ∪ (0; 1)
D. (0;1)
Lời giải:
Ta có
Bảng xét dấu đạo hàm
Hàm số nghịch biến trên các khoảng (-∞; -1) và (0; 1)
Đáp án cần chọn là: A
Câu 16: Cho hàm số
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số (1) nghịch biến trên R\{1}
B. Hàm số (1) nghịch biến trên (-∞; 1) và (1; +∞)
C. Hàm số (1) nghịch biến trên (-∞; 1) ∪ (1; +∞)
D. Hàm số (1) đồng biến trên (-∞; 1) và (1; +∞)
Lời giải:
Hàm số
xác định ∀x ≠ 1
Ta có:
xác định ∀x ≠ 1
Bảng xét dấu đạo hàm
Hàm số nghịch biến trên các khoảng (-∞ 1) và (1; +∞)
Đáp án cần chọn là: B
Câu 17: Tìm khoảng đồng biến của hàm số f(x)= x + cos2x
A. R\{0}
B. (-∞; +∞)
C. (-1; 1)
D. (0; π)
Lời giải:
f'(x) = 1 - 2sinxcosx = sin2x + cos2x - 2.sinx.cosx = (sinx - cosx)2 ≥ 0 ∀x ∈ R
Hàm số đồng biến trên khoảng (-∞; +∞)
Đáp án cần chọn là: B
Câu 18: Hàm số:
đồng biến trên khoảng nào?
A. R B. (-∞; 0) C. (-1; 0) D. (0; +∞)
Lời giải:
Hàm số đồng biến trên R
Đáp án cần chọn là: A
Câu 19: Hàm số y=2x4+1 đồng biến trên khoảng nào?
Lời giải:
Ta có y′=8x3=0⇔x=0;y′>0⇔x>0
Vậy hàm số đã cho đồng biến trên (0;+∞)
Đáp án cần chọn là: A
Câu 20: Hình bên là đồ thị hàm số y=f′(x). Hỏi hàm số y=f(x) đồng biến trên khoảng nào dưới đây?
Lời giải:
Hàm số y=f′(x) dương trong khoảng (2;+∞)
⇒ Hàm số đồng biến trên (2;+∞)
Đáp án cần chọn là: C
Câu 21: Khẳng định nào sau đây là đúng về tính đơn điệu của hàm số y=x3−3x2+1?
Lời giải:
Ta có:
y′=3x2−6x=0⇔[x=0x=2
y′>0⇔[x>2x<0 nên hàm số đồng biến trên các khoảng (−∞;0) và (2;+∞).
y′<0⇔0<x<2 nên hàm số nghịch biến trên (0;2).
Đáp án cần chọn là: B
Câu 22: Cho hàm số y=x+3x+2. Khẳng định nào sau đây đúng?
Lời giải:
TXĐ: D=R∖{−2}.
Có y′=1.2−3.1(x+2)2=−1(x+2)2<0∀x∈D
⇒Hàm số nghịch biến trên mỗi khoảng (−∞;−3) và (−2;+∞).
Đáp án cần chọn là: B
Câu 23: Cho hàm số y = x3 + 3x2 – 9x – 7. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số nghịch biến trên khoảng (-3;1) .
B. Hàm số đồng biến trên (-9;-5).
C. Hàm số đồng biến trên R.
D. Hàm số đồng biến trên (5;+∞).
Lời giải:
Tập xác định: D = R.
Ta có: 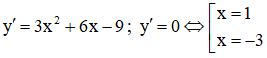
Bảng biến thiên:
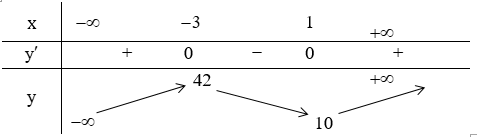
Kết luận: Hàm số đồng biến trên các khoảng: (-∞;-3),(1;+∞) . Hàm số nghịch biến trên khoảng (-3;1)
Đáp án cần chọn là: C
Câu 24. Các khoảng nghịch biến của hàm số y = -x4 + 2x2 - 4 là
A. (-1;0) và (1;+∞)
B. (-∞;1) và (1;+∞)
C. (-1;0) và (0;1)
D. (-∞;1) và (0;1)
Lời giải:
Tập xác định: D = R.
Ta có: 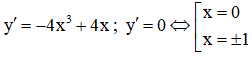
Bảng biến thiên
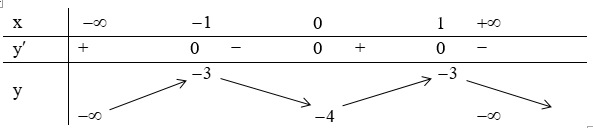
Kết luận: Hàm số đồng biến trên các khoảng: (-∞;1), (0;1) . Hàm số nghịch biến trên các khoảng: (-1;0), (1;+∞)
Đáp án cần chọn là: A
Câu 25. Chọn mệnh đề đúng về hàm số 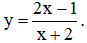
A. Hàm số nghịch biến trên từng khoảng xác định của nó.
B. Hàm số đồng biến trên tập xác định của nó.
C. Hàm số đồng biến trên từng khoảng xác định của nó.
D. Hàm số nghịch biến trên tập xác định của nó.
Lời giải:
Tập xác định: D = R\{-2} .Ta có: 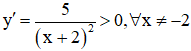 . Nên hàm số đồng biến trên từng khoảng xác định của nó.
. Nên hàm số đồng biến trên từng khoảng xác định của nó.
Bảng biến thiên
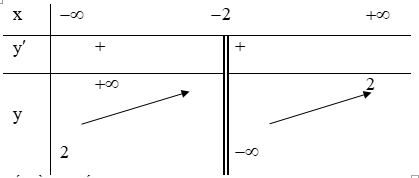
Kết luận: hàm số đồng biến trên từng khoảng xác định.
Đáp án cần chọn là: C
Câu 26. Cho hàm số 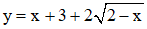 . Khẳng định nào sau đây là khẳng đúng
. Khẳng định nào sau đây là khẳng đúng
A. Hàm số đồng biến trên khoảng (-∞;-2) và nghịch biến trên khoảng (-2;2)
B. Hàm số đồng biến trên khoảng (-∞;1) và nghịch biến trên khoảng (1;2)
C. Hàm số nghịch biến trên khoảng (-∞;-2) và đồng biến trên khoảng (-2;2)
D. Hàm số nghịch biến trên khoảng (-∞;1) và đồng biến trên khoảng (1;2)
Lời giải:
Tập xác định: D = (-∞;2] .
Đạo hàm: 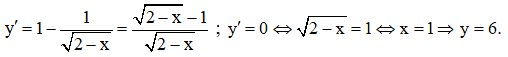
Bảng biến thiên:
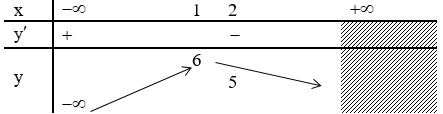
Kết luận: hàm số đã cho đồng biến trên khoảng (-∞;1) và nghịch biến trên khoảng (1;2)
Đáp án cần chọn là: B
Câu 27. Cho hàm số 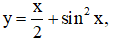 với x ∈ [0;π] . Mệnh đề nào sau đây đúng?
với x ∈ [0;π] . Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên [0;π]
B. Hàm số nghịch biến trên [0;π]
C. Hàm số nghịch biến trên 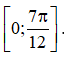
D. Hàm số nghịch biến trên 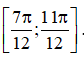
Lời giải:
Tập xác định: D = [0;π]
Đạo hàm: 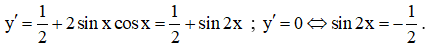
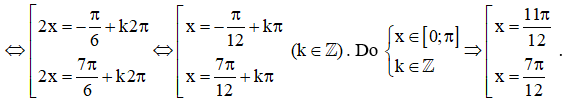
Bảng biến thiên
Đáp án cần chọn là: D
Câu 28. Cho hàm số y = f(x) có bảng biến thiên như hình bên. Hàm số y = -2018.f(x) đồng biến trên khoảng nào dưới đây?
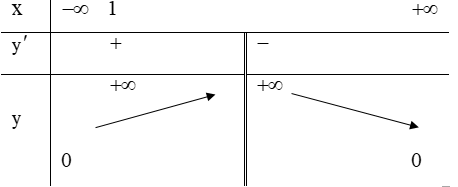
A. (-∞;0)
B. (1;+ ∞)
C. (0;+ ∞)
D. (-∞;1)
Lời giải:
Đặt g(x) = -2018.f(x), ta có: g'(x) = -2018.f'(x).
Xét g'(x) = -2018.f'(x) ≥ 0 ⇔ f'(x) ≤ 0 ⇔ x ≥ 1
Vậy hàm số y = -2018.f(x) đồng biến trên khoảng (1;+ ∞)
Đáp án cần chọn là: B
Câu 29. Cho hàm số f(x) , bảng xét dấu của f'(x) như sau:
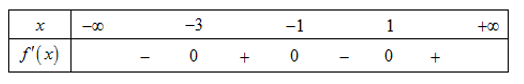
Hàm số f(5 - 2x) nghịch biến trên khoảng nào dưới đây?
A. (2;3).
B. (0;2).
C. (3;5).
D. (5;+∞).
Lời giải:
Ta có y = f(5 - 2x) → y' = -2f'(5 - 2x)
Hàm số nghịch biến khi y' = -2f'(5 - 2x) ≤ 0 ⇔ f'(5 - 2x) ≥ 0
Dựa vào bảng xét dấu ta thấy khi 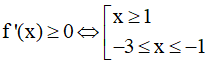
Nên 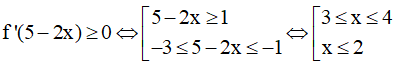
Vậy hàm số y = f(5 - 2x) nghịch biến trên các khoảng (3,4) và (-∞;2)
Đáp án cần chọn là: B
Câu 30. Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau:

Hàm số y = 3f(x + 2) - x3 + 3x đồng biến trên khoảng nào dưới đây?
A. (5;+∞)
B. (-∞;-1)
C. (-1,0)
D. (0,2)
Lời giải:
Ta có y' = 3f'(x + 2) - 3x2 + 3 = 3[f'(x + 2) + (1 - x2)]
Xét f'(x + 2) = 0 ⇔ x + 2 ∈ ⇔ x ∈ {-1,0,1,2}
Xét 1 - x2 = 0 ⇔ x = 1, x = -1
Lại có: 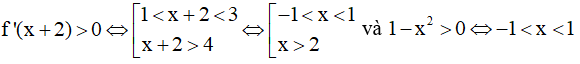
Bảng xét dấu
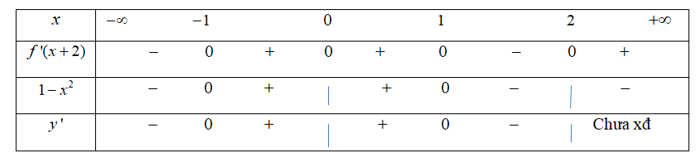
Từ bảng xét dấu suy ra trên khoảng (-1,0) hàm số đồng biến.
Đáp án cần chọn là: C
Câu 31. Cho hàm số y = f(x) có đạo hàm trên R. Hàm số y = f'(3x - 1) có đồ thị như hình vẽ:
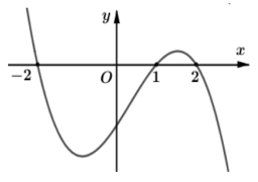
Hàm số đồng biến trên khoảng nào dưới đây?
A. (2,6)
B. (-∞;-7)
C. (-∞;-6)
D. 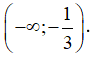
Lời giải:
Ta cần giải BPT dạng f'(x) > 0.
Ta có 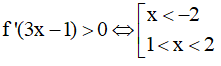
Đặt 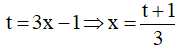
Do đó: 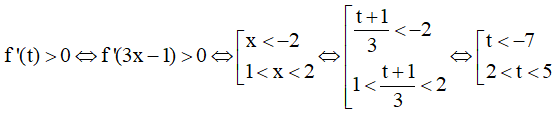
Vậy 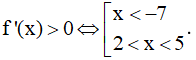
Đáp án cần chọn là: B
Câu 32. Cho hàm số y = -x3 - mx2 + (4m + 9)x + 5 với m là tham số. Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng (-∞;+∞)
A. 4
B. 6
C. 7
D. 5
Lời giải:
TXĐ: D = R .
Đạo hàm y' = -3x2 - 2mx + 4m + 9
Để hàm số đã cho nghịch biến trên khoảng (-∞;+∞) ⇔ y' ≤ 0,∀x ∈ R
( y' = 0 có hữu hạn nghiệm).
Do a = -3 < 0 nên y’ ≤ 0 ⇔ Δ' ≤ 0 ⇔ m2 + 3(4m + 9) ≤ 0 ⇔ -9 ≤ m ≤ -3.
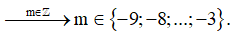
Vậy có 7 giá trị m thoả mãn điều kiện bài toán.
Đáp án cần chọn là: C
Câu 33. Hàm số 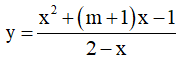 ( m là tham số) nghịch biến trên mỗi khoảng xác định của nó khi các giá trị của m là:
( m là tham số) nghịch biến trên mỗi khoảng xác định của nó khi các giá trị của m là:
A. m ≥ 1 .
B. m = 1
C. 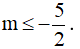
D. -1 < m < 1
Lời giải:
Tập xác định: D = R\.
Đạo hàm: 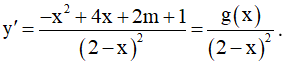
Hàm số nghịch biến trên mỗi khoảng xác định của nó khi và chỉ khi y' ≤ 0,∀x ∈ R
(Dấu '' = '' chỉ xảy ra tại hữu hạn điểm trên D )
⇔ g(x) = -x2 + 4x + 2m + 1 ≤ 0, ∀x ∈ D .
Do a = -1 < 0, nên g(x) ≤ 0 .
⇔ Δg' ≤ 0 ⇔ 4 - (-1).(2m + 1) ≤ 0 ⇔ 2m + 5 ≤ 0 ⇔ 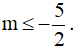
Đáp án cần chọn là: C
Câu 34: Cho hàm số y=f(x) xác định trên D. Nếu với mọi x1,x2∈D mà x1<x2 ta đều có f(x1)<f(x2) thì:
Lời giải:
Hàm số y=f(x) thỏa mãn nếu với mọi x1,x2∈D mà x1<x2 ta đều có f(x1)<f(x2) thì hàm số đồng biến trên D
Đáp án cần chọn là: A
Câu 35: Cho hàm số f(x) xác định và có đạo hàm trên (a;b). Nếu f′(x)<0,∀x∈(a;b) thì:
Lời giải:
Sử dụng định lý về xét tính đồng biến, nghịch biến của hàm số trên một khoảng đã nêu ở phần phương pháp, ở đây khoảng K=(a;b) ta được:
Hàm số y=f(x) xác định và có đạo hàm f′(x)<0,∀x∈(a;b) thì f(x) nghịch biến trên (a;b).
Đáp án cần chọn là: B
Câu 36: Cho hàm số f(x) có đạo hàm trên R. Nếu hàm số f(x) nghịch biến trên R thì:
Lời giải:
Hàm số y=f(x) nghịch biến trên R thì f′(x)≤0,∀x∈R.
Đáp án cần chọn là: D
Câu 37: Cho hàm số f(x) có đạo hàm trên R. Nếu hàm số f(x) đồng biến trên R thì:
Lời giải:
Hàm số y=f(x) đồng biến trên R thì f′(x)≥0,∀x∈R.
Đáp án cần chọn là: A
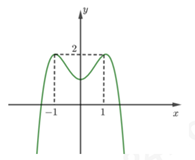
Câu 38: Cho hàm số y=f(x) có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Lời giải:
Trong khoảng từ (0;1) đồ thị hàm số đi lên nên f(x) đồng biến trên khoảng (0;1).
Đáp án cần chọn là: C
Câu 39: Cho hàm số: f(x)=−2x3+3x2+12x−5. Trong các mệnh đề sau, tìm mệnh đề sai?
Lời giải:
f(x)=−2x3+3x2+12x−5⇒f′(x)=−6x2+6x+12=0⇔x=2;x=−1
Ta có: y′<0,∀x∈(−∞;−1)∪(2;+∞) nên hàm số nghịch biến trên các khoảng (−∞;−1);(2;+∞) và y′>0,∀x∈(−1;2) nên nó đồng biến trên khoảng (−1;2).
Đối chiếu với các đáp án đã cho ta thấy các Đáp án A, B, C đều đúng vì các khoảng đó đều là khoảng nằm trong khoảng nghịch biến hoặc đồng biến của hàm số, chỉ có đáp án D sai.
Đáp án cần chọn là: D
Câu 40: Cho hàm số có bảng biến thiên như sau:
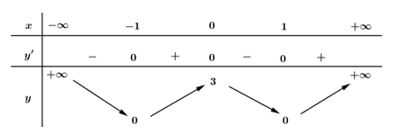
Mệnh đề nào dưới đây đúng?
Lời giải:
Dựa vào bàng biến thiên ta thấy hàm số đồng biến trên các khoảng (−1;0) và (1;+∞).
Hàm số nghịch biến trên các khoảng (−∞;−1) và (0;1).
Đáp án cần chọn là: A
Câu 41: Gọi S là tập hợp các giá trị nguyên dương của m để hàm số y=x3−3(2m+1)x2+(12m+5)x+2 đồng biến trên khoảng (2;+∞). Số phần tử của S bằng:
Lời giải:
Xét hàm số: y=x3−3(2m+1)x2+(12m+5)+2
⇒y′=3x2−6(2m+1)x+12m+5⇒y′=0⇔3x2−6(2m+1)x+12m+5=0(∗)
TH1: Hàm số đã cho đồng biến trên R
⇔y′≥0∀x⇔Δ′≤0⇔9(2m+1)2−3(12m+5)≤0⇔9(4m2+4m+1)−36m−15≤0⇔36m2−6≤0⇔m2≤16⇔−√66≤m≤√66
TH2: Hàm số đã cho đồng biến trên (2;+∞)
⇔(∗) có hai nghiệm phân biệt x1,x2 thỏa mãn 2≤x1<x2
⇔{Δ′>0(x1−2)(x1−2)≥0x1+x2>4⇔{36m2−6>0x1x2−2(x1+x2)+4≥0x1+x2>4⇔{m2>1612m+53−2.6(2m+1)3+4≥06(2m+1)3>4⇔{[m>√66m<−√6612m+5−24m−2+12≥04m+2>4⇔{[m>√66m<−√66−12m≥−15m>12⇔{[m>√66m<−√66m≤54m>12⇔12<m≤54
Kết hợp hai trường hợp ta được: [−√66≤m≤√6612<m≤54
Lại có: m∈Z+ ⇒m=1.
Vậy có 1 giá trị m thỏa mãn bài toán.
Đáp án cần chọn là: A
Câu 42: Cho hàm số y=x4−2x2+15. Hàm số đồng biến trên khoảng nào dưới đây?
B. (0;1)
Lời giải:
Đạo hàm: y′=4x3−4x.
Hàm số đồng biến khi và chỉ khi:
y′=4x3−4x>0⇔4x(x2−1)>0⇔[x>1−1<x<0 ⇒x∈(−1;0)∪(1;+∞)
Do đó hàm số đồng biến trên các khoảng (−1;0) và (1;+∞)
Đáp án cần chọn là: A
Câu 43: Hàm số y=−x4+2x3−2x−1 nghịch biến trên khoảng nào sau đây ?
Lời giải:
Ta có y′=−4x3+6x2−2;∀x∈R.
Khi đó y′=0⇔−4x3+6x2−2=0⇔−2(x−1)2(2x+1)=0⇔[x=−12x=1
Bảng biến thiên:
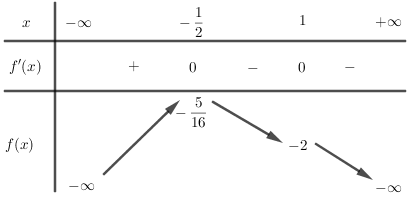
Suy ra hàm số đã cho nghịch biến trên khoảng (−12;+∞).
Đáp án cần chọn là: A
Câu 44: Cho hàm số: f(x)=−2x3+3x2+12x−5. Trong các mệnh đề sau, tìm mệnh đề sai?
Lời giải:
f(x)=−2x3+3x2+12x−5⇒f′(x)=−6x2+6x+12=0⇔x=2;x=−1
Ta có: y′<0,∀x∈(−∞;−1)∪(2;+∞) nên hàm số nghịch biến trên các khoảng (−∞;−1);(2;+∞) và y′>0,∀x∈(−1;2) nên nó đồng biến trên khoảng (−1;2).
Đối chiếu với các đáp án đã cho ta thấy các Đáp án A, B, C đều đúng vì các khoảng đó đều là khoảng nằm trong khoảng nghịch biến hoặc đồng biến của hàm số, chỉ có đáp án D sai.
Đáp án cần chọn là: D
Câu 45:Cho hàm số y=f(x) xác định và có đạo hàm f′(x)=2x2 trên R. Chọn kết luận đúng:
Lời giải:
Ta có: f′(x)=2x2≥0,∀x∈R và f′(x)=0⇔x=0 nên hàm số đồng biến trên R.
Đáp án cần chọn là: A
Câu 46:
Cho hàm số f(x) có đạo hàm liên tục trên R và có đồ thị của hàmy=f′(x) như hình vẽ. Xét hàm số g(x)=f(x2−2). Mệnh đề nào dưới đây sai ?
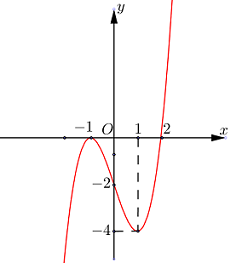
Lời giải:
Ta có: g′(x)=2xf′(x2−2)
Cho g′(x)=0⇔[x=0x2−2=−1x2−2=2⇔[x=0x=±1x=±2.
Vì -1 là điểm cực đại của f′(x) nên ±1 là điểm cực đại của f′(x2−2). Do đó f′(x2−2) không đổi dấu qua ±1 và luôn mang dấu dương.
Bảng xét dấu g′(x):
![]()
Vậy hàm số g(x) nghịch biến trên (−1;0) là phát biểu sai.
Đáp án cần chọn là: C
Câu 47: Cho hàm số y=f(x) xác định và có đạo hàm f′(x)=(1−√2)x2 trên R. Chọn kết luận đúng:
Lời giải:
Ta có: f′(x)=(1−√2)x2≤0,∀x∈R và f′(x)=0⇔x=0 nên hàm số nghịch biến trên R.
Đáp án cần chọn là: C
Câu 48:Cho hàm số y=f(x) xác định và có đạo hàm trên (a;b). Chọn kết luận đúng:
Lời giải:
Đáp án A: Nếu f′(x)≥0,∀x∈(a;b) thì f(x) chưa chắc đã đồng biến trên (a;b), chẳng hạn hàm số y=f(x)=2 có f′(x)=0≥0,∀x nhưng đây là hàm hằng nên không đồng biến, do đó A sai.
Đáp án B: Nếu f′(x)>0,∀x∈(a;b) thì f(x) đồng biến trên (a;b) đúng.
Đáp án C: Nếu f′(x)=0,∀x∈(a;b) thì f(x) không đổi trên (a;b), chưa chắc nó đã có giá trị bằng 0 nên C sai.
Đáp án D: Nếu f′(x)≤0,∀x∈(a;b) thì f(x) không đổi trên (a;b) sai.
Đáp án cần chọn là: B
Câu 49: Cho bất phương trình 3√x4+x2+m−3√2x2+1+x2(x2−1)>1−m. Tìm tất cả các giá trị thực của tham số m để bất phương trình nghiệm đúng với mọi x>1.
Lời giải:
Ta có 3√x4+x2+m−3√2x2+1+x2(x2−1)>1−m
⇔3√x4+x2+m−3√2x2+1+x4−x2>1−m
⇔3√x4+x2+m+x4+x2+m>3√2x2+1+2x2+1 (*)
Xét hàm số f(t)=t3+t⇒y′=2t2+1>0 nên hàm số f(t) là hàm đồng biến
Khi đó phương trình (*) trở thành:
f(3√x4+x2+m)>f(3√2x2+1) ⇔3√x4+x2+m>3√2x2+1 ⇔x4+x2+m>2x2+1 ⇔m>−x4+x2+1
Xét hàm số g(x)=−x4+x2+1 với x>1
Có g′(x)=−4x3+2x=−2x(2x2−1)<0;∀x>1
Ta có BBT của hàm g(x)=−x4+x2+1 với x>1
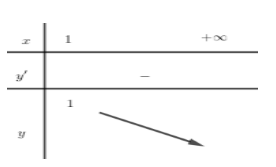
Từ BBT suy ra m≥1.
Đáp án cần chọn là: D
Câu 50: Cho hàm số y=f(x) có đạo hàm trên (a;b). Phát biểu nào sau đây là sai?
Lời giải:
Cho hàm số y=f(x) có đạo hàm trên (a;b). Khi đó
Hàm số y=f(x) gọi là nghịch biến trên (a;b) khi và chỉ khi f′(x)≤0,∀x∈(a;b) và f′(x)=0 tại hữu hạn giá trị x∈(a;b) nên D sai.
Các đáp án A, B, C đều đúng.
Đáp án cần chọn là: D
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.