Toptailieu.vn giới thiệu Giải bài tập Toán 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Căn bậc hai lớp 12.
Giải bài tập Toán 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Trả lời câu hỏi giữa bài:
Câu hỏi 1 trang 20 SGK Giải tích 12: Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) trên đoạn ;b) trên đoạn [3; 5].
Phương pháp giải:
Tính ,
+ => Hàm số nghịch biến trên. Đạt GTLN tại x = a, đạt GTNN tại x = b.
+ => Hàm số đồng biến trên. Đạt GTLN tại x = b, đạt GTNN tại x = a.
Lời giải:
trên đoạn .
Vậy hàm số nghịch biến trên đoạn .
Khi đó trên đoạn : hàm số đạt giá trị lớn nhất tại và giá trị lớn nhất bằng 9, hàm số đạt giá trị nhỏ nhất tại và giá trị nhỏ nhất là 0.
b) trên đoạn
Vậy hàm số nghịch biến trên đoạn
Khi đó trên đoạn : hàm số đạt giá trị lớn nhất tại và giá trị lớn nhất bằng , hàm số đạt giá trị nhỏ nhất tại và giá trị nhỏ nhất
Câu hỏi 2 trang 21 SGK Giải tích 12 : Cho hàm số:
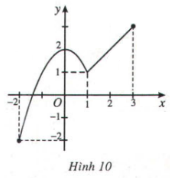
Có đồ thị như Hình 10. Hãy chỉ ra giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-2; 3] và nêu cách tính.
Phương pháp giải:
Quan sát đồ thị,đoạn , tìm điểm có tung độ y lớn nhất (nhỏ nhất) từ đó kết luận GTLN (GTNN)
Lời giải:
Trên đoạn , điểm thấp nhất của đồ thị hàm số có tọa độ là và điểm cao nhất có tọa độ .
Vậy GTLN là và GTNN là .
Câu hỏi 3 trang 23 SGK Giải tích 12: Lập bảng biến thiên của hàm số
Từ đó suy ra giá trị nhỏ nhất của trên tập xác định.
Phương pháp giải:
+) Tìm tập xác định của hàm số.
+) Tính đạo hàm của hàm số. Tìm các điểm mà tại đó đạo hàm bằng 0 hoặc không xác định
+) Sắp xếp các điểm theo thứ tự tăng dần và lập bảng biến thiên
+) Dựa vào bảng biến thiên, khoảng đồng biến và nghịch biến của hàm số trên tập xác định của nó để suy ra GTNN
Lời giải:
1. TXĐ:
2.
Cho thì .
3. Bảng biến thiên
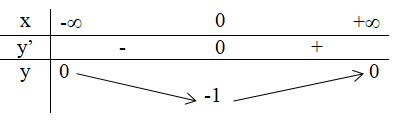
Vậy giá trị nhỏ nhất của hàm số đã cho là tại
Bài tập trang 23-24 SGK Toán 12
Bài 1 trang 23 SGK Giải tích 12: Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) trên các đoạn và
b) trên các đoạn và
c) trên các đoạn và
d) trên đoạn .
Phương pháp giải:
Để tìm GTLN, GTNN của hàm số trên đoạn ta làm như sau :
+) Tìm các điểm thuộc đoạn mà tại đó hàm số có đạo hàm hoặc không có đạo hàm.
+) Tính và
+) So sánh các giá trị tìm được ở trên. Giá trị lớn nhất trong các giá trị đó chính là GTLN của hàm số trên và giá trị nhỏ nhất trong các giá trị đó chính là GTNN của hàm số trên .
Lời giải:
a)
+) Xét có :
Ta có :
Vậy và
+) Xét có:
Ta có :
Vậy và
b)
Ta có:
+) Xét có:
Có:
Vậy và
+) Xét ta thấy
Có
Vậy và
c) . Tập xác định:
Ta có:
+) Với có:
Vậy và
+) Với có:
Vậy và
d) . Tập xác định:
Xét tập
Có:
Ta có:
Vậy và
Bài 2 trang 24 SGK Giải tích 12: Trong số các hình chữ nhật cùng có chu vi , hãy tìm hình chữ nhật có diện tích lớn nhất.
Phương pháp giải:
Cho hình chữ nhật có chiều dài là x và chiều rộng là y.
+) Chu vi hình chữ nhật:
+) Diện tích hình chữ nhật:
Lập hàm số diện tích , xét hàm suy ra GTLN.
Lời giải:
Gọi chiều rộng và chiều dài của hình chữ nhật lần lượt là
Chu vi của hình chữ nhật là
Khi đó:
Diện tích:
Xét hàm số: trên ta có:
Ta có:
khi .
Vậy hình chữ nhật có diện tích lớn nhất là hình vuông có cạnh là
Cách khác:
Ta có:
Bài 3 trang 24 SGK Giải tích 12: Trong tất cả các hình chữ nhật cùng có diện tích , hãy xác định hình chữ nhật có chu vi nhỏ nhất.
Phương pháp giải:
+) Cho hình chữ nhật có chiều dài là và chiều rộng là
+) Chu vi của hình chữ nhật đó là:
+) Diện tích của hình chữ nhật đó là:
Lập hàm số , xét hàm suy ra GTNN.
Lời giải:
Gọi chiều rộng và chiều dài của hình chữ nhật lần lượt là
Theo đề bài ta có diện tích hình chữ nhật là
Chu vi hình chữ nhật đó là:
Xét hàm số trên ta có:
Ta có:
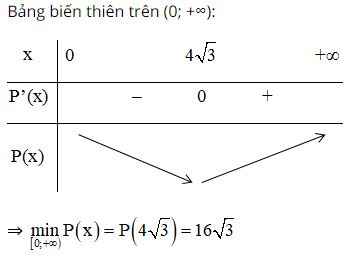
Vậy hình chữ nhật có chu vi nhỏ nhất là hình vuông có cạnh
Bài 4 trang 24 SGK Giải tích 12: Tính giá trị lớn nhất của các hàm số sau:
a) ;b)
Phương pháp giải:
Để tìm GTLN, GTNN của hàm số trên đoạn ta làm như sau :
+) Tìm các điểm thuộc đoạn mà tại đó hàm số có đạo hàm hoặc không có đạo hàm.
+) Tính và
+) So sánh các giá trị tìm được ở trên. Giá trị lớn nhất trong các giá trị đó chính là GTLN của hàm số trên và giá trị nhỏ nhất trong các giá trị đó chính là GTNN của hàm số trên .
Quy ước : Nếu đề bài yêu cầu tìm GTLN và GTNN của hàm số nhưng không chỉ rõ tìm GTLN và GTNN trên tập nào thì ta hiểu là GTLN và GTNN trên tập xác định của hàm số
Lời giải:
a)
Tập xác định:
Ta có:
Ta có bảng biến thiên:
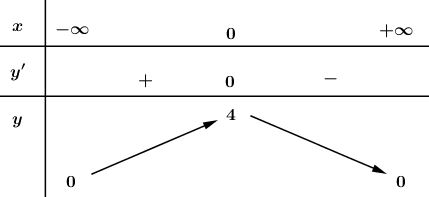
Từ bảng biến thiên ta thấy hàm số đạt GTLN tại
Cách khác:
Ta thấy: nên .
Vậy . Dấu "=" xảy ra khi .
b)
Tập xác định:
Ta có:
Ta có bảng biến thiên:
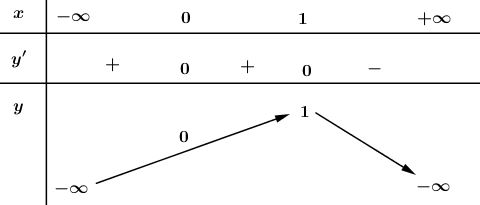
Theo bảng biến thiên ta thấy hàm số đạt GTLN tại .
Bài 5 trang 24 SGK Giải tích 12: Tính giá trị nhỏ nhất của các hàm số sau:
Phương pháp giải:
- Phá dấu giá trị tuyệt đối đưa hàm số về dạng khoảng.
- Lập bảng biến thiên và kết luận.
Lời giải:
a)
Ta có:
Tập xác định:
Ta có bảng biến thiên:
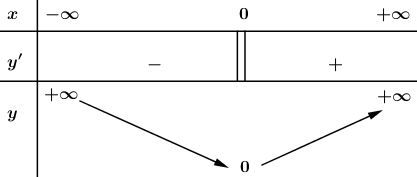
Từ bảng biến thiên ta có hàm số đạt GTNN tại
b)
Ta có:
Bảng biến thiên:
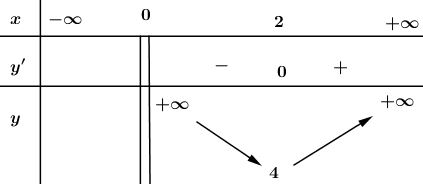
Từ bảng biến thiên ta thấy:
Cách khác:
Áp dụng BĐT Cô-si ta có:
khi .
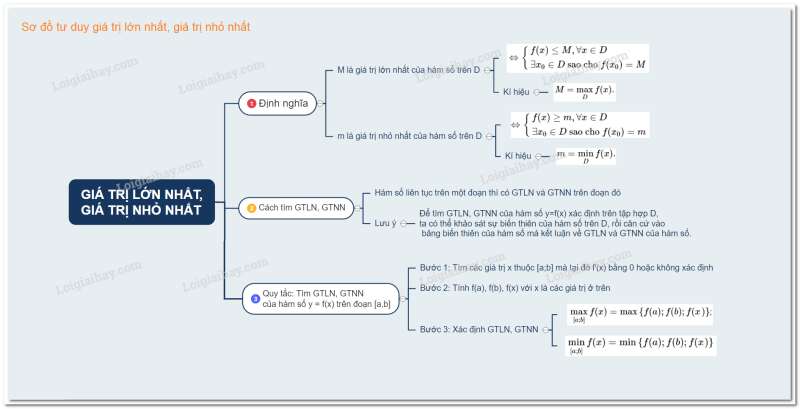
Lý thuyết Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1. Định nghĩa
Cho hàm số xác định trên tập
- Số là giá trị lớn nhất (GTLN) của hàm số trên
Kí hiệu :
- Số là giá trị nhỏ nhất (GTNN) của hàm số trên
Kí hiệu:
2. Cách tính giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn
Định lí
Hàm số liên tục trên một đoạn thì có GTLN và GTNN trên đoạn đó.
Quy tắc tìm GTLN, GTNN của hàm số liên tục trên đoạn [a ; b]
- Tìm các điểm mà tại đó hoặc không xác định.
- Tính
- Khi đó: ;
3. Chú ý
Để tìm GTLN, GTNN của hàm số xác định trên tập hợp , ta có thể khảo sát sự biến thiên của hàm số trên rồi căn cứ vào bảng biến thiên của hàm số mà kết luận về GTLN và GTNN của hàm số.a) ;b) .
Các dạng toán về giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Dạng 1: Tìm GTLN, GTNN của hàm số trên một đoạn.
Cho hàm số xác định và liên tục trên đoạn
Phương pháp:
- Bước 1: Tính , giải phương trình tìm các nghiệm thỏa mãn
- Bước 2: Tính các giá trị
- Bước 3: So sánh các giá trị tính được ở trên và kết luận:
+ Giá trị lớn nhất tìm được trong số các giá trị ở trên là GTLN của hàm số trên
+ Giá trị nhỏ nhất tìm được trong số các giá trị ở trên là GTNN của hàm số trên
Dạng 2: Tìm GTLN, GTNN của hàm số trên một khoảng.
Cho hàm số xác đinh và liên tục trên
Phương pháp:
- Bước 1: Tính , giải phương trình tìm các nghiệm thỏa mãn
- Bước 2: Tính các giá trị và
- Bước 3: So sánh các giá trị tính được và kết luận.
+ Nếu GTLN (hoặc GTNN) trong số các giá trị ở trên là hoặc thì kết luận hàm số không có GTLN (hoặc GTNN) trên khoảng
+ Nếu GTLN (hoặc GTNN) trong số các giá trị ở trên là thì kết luận hàm số đạt GTLN (hoặc GTNN) bằng khi
Dạng 3: Tìm điều kiện của tham số để hàm số có GTLN, GTNN thỏa mãn điều kiện cho trước
Cho hàm số xác đinh và liên tục trên đoạn
Phương pháp: (chỉ áp dụng cho một số bài toán dễ dàng tìm được nghiệm của )
- Bước 1: Tính , giải phương trình tìm các nghiệm
- Bước 2: Tính các giá trị
- Bước 3: Biện luận theo tham số để tìm GTLN, GTNN của hàm số trên đoạn
- Bước 4: Thay vào điều kiện bài cho để tìm