Toptailieu.vn giới thiệu Giải bài tập Toán lớp 10 Bài 23: Quy tắc đếm sách Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10 Tập 2. Mời các bạn đón xem:
Toán 10 Kết nối tri thức Bài 23: Quy tắc đếm
1. Quy tắc cộng và sơ đồ hình cây
HĐ1 trang 61 SGK Toán 10 Tập 2: Chọn chuyến đi (H.8.1)
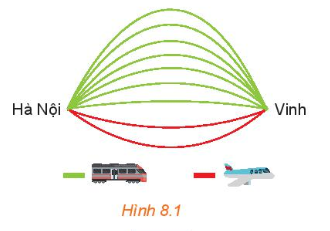
Từ Hà Nội vào Vinh mỗi ngày có 7 chuyến tàu hỏa và 2 chuyến máy bay. Bạn An muốn ngày Chủ nhật này đi từ Hà Nội vào Vinh bằng tàu hỏa hoặc máy bay.
Hỏi bạn An có bao nhiêu cách chọn?
Lời giải:
Để đi bằng tàu hỏa bạn An có 7 cách chọn và đi bằng máy bay có 2 cách chọn.
Vậy bạn An có tất cả 7+2=9 cách chọn chuyến đi
HĐ2 trang 61 SGK Toán 10 Tập 2: Chọn vé tàu (H.8.2)
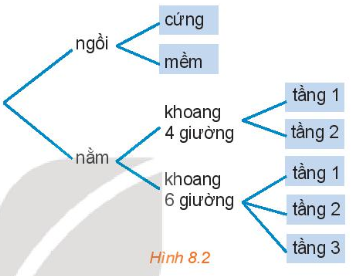
Bạn An đã quyết định mua vé tàu đi từ Hà Nội vào Vinh trên chuyến tàu SE7. Trên tàu có các toa ghế ngồi và các toa giường nằm. Toa ngồi có 2 loại vé: ngồi cứng và ngồi mềm. Toa nằm có loại không 4 giường và loại khoang 6 giường. Khoang 4 giường có hai loại vé: tầng 1 và tầng 2, khoang 6 giường có ba loại vé: tầng 1, tầng 2, tầng 3. Hỏi:
a) Có bao nhiêu loại vé ghế ngồi và bao nhiêu loại vé giường nằm?
b) Có bao nhiêu loại vé để bạn An lựa chọn?
Lời giải:
a) Số vé ghế ngồi là 2 (loại vé)
Số vé giường nằm là 2+3=5 (loại vé)
b) Số loại vé để bạn An lựa chọn là:
2+5=7 (loại vé)
Phương pháp giải:
- không nguyên tố cùng nhau = có ước chung (khác 1).
- Mà 35 =5.7 nên ta tìm các số chia hết cho 5 hoặc 7.
Lời giải:
Từ 1 đến 30 có:
- Có 6 số chia hết cho 5 là: 5, 10, 15, 20, 25, 30.
- Có 4 số chia hết cho 7 là: 7, 14, 21, 28.
Có tất cả 6+4= 10 số tự nhiên không nguyên tố cùng nhau với 35.
2. Quy tắc nhân
HĐ3 trang 62 SGK Toán 10 Tập 2: Thầy Trung muốn đi từ Hà Nội vào Huế, rồi từ Huế vào Quảng Nam. Biết rằng từ Hà Nội vào Huế có thể đi bằng 3 cách: ô tô, tàu hỏa hoặc máy bay. Còn từ Huế vào Quảng Nam có thể đi bằng 2 cách: ô tô hoặc tàu hỏa.
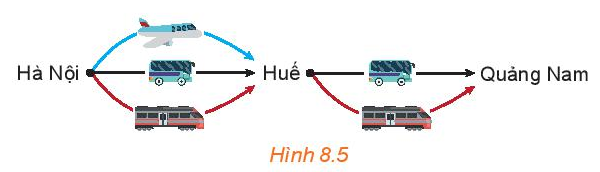
Hỏi thầy Trung có bao nhiêu cách chọn phương tiện để đi từ Hà Nội vào Quảng Nam?
Lời giải:
Đi từ Hà Nội vào Huế, rồi từ Huế vào Quảng Nam có các cách là:
Máy bay >> Oto
Máy bay >> tàu hỏa
Oto >> Oto
Oto >> tàu hỏa
Tàu hỏa >> Oto
Tàu hỏa >> tàu hỏa
Vậy thầy Trung có 6 cách chọn phương tiện để đi từ Hà Nội vào Quảng Nam.
HĐ4 trang 63 SGK Toán 10 Tập 2: Để lắp ghế vào một phòng chiếu phim, các ghế được gắn nhãn bằng một chữ cái in hoa (trong bảng 26 chữ cái tiếng Anh Từ A đến Z) đứng trước và một số nguyên từ 1 đến 20, chẳng hạn X15, Z2,...
Hỏi có thể gắn nhãn tối đa được cho bao nhiêu ghế?
Lời giải:
Để gắn nhãn cho các ghế ta chọn chọn 1 chữ cái in hoa và 1 số (từ 1 đến 20).
Số cách chọn chữ cái in hoa: 26 cách (tương ứng với 26 chữ)
Số cách chọn số: 20 cách
Vậy số ghế gắn nhãn tối đa là 26.20 = 520 (ghế)
Luyện tập 2 trang 64 SGK Toán 10 Tập 2: Tại kì World Cup năm 2018, vòng bảng gồm có 32 đội tham gia, được chia vào 8 bảng, mỗi bảng 4 đội thi đấu vòng tròn (mỗi đội chơi một trận với từng đội khác trong cùng bảng). Hỏi tổng cộng vòng bảng có bao nhiêu trận đấu?
Lời giải:
- Mỗi bảng 4 đội thi đấu vòng tròn, giả sử là các đội A, B, C, D
Các trận đấu là: A-B, A-C, A-D, B-C, B-D, C-D => có tất cả 6 trận đấu
- Có 8 bảng khác nhau.
- Tổng cộng vòng bảng có số trận đấu là 6.8=48 (trận đấu).
3. Kết hợp quy tắc cộng và quy tắc nhân
a) Là số tự nhiên có ba chữ số khác nhau?
b) Là số tự nhiên chẵn có ba chữ số khác nhau?
Lời giải:
a) Từ 4 chữ số 0, 1, 2, 3:
- Hàng trăm có 3 cách chọn.
- Hàng chục có 3 cách chọn.
- Hàng đơn vị có 2 cách chọn.
Vậy có tất cả 3.3.2=18 số tự nhiên khác nhau có 3 chữ số được lập từ 0, 1, 2, 3.
b) - Trường hợp 1: hàng đơn vị là số 0 như vậy hàng trăm có 3 cách chọn, hàng chục có 2 cách chọn.
Có tất cả 1. 2. 3= 6 số có thể lập được.
- Trường hợp 2: hàng đơn vị là số 2 như vậy hàng trăm có 2 cách chọn, hàng chục có 2 cách chọn.
Có tất cả 1. 2. 2= 4 số có thể lập được.
Vậy có thể lập 6+4= 10 số tự nhiên chẵn có ba chữ số khác nhau.
Vận dụng trang 65 SGK Toán 10 Tập 2: Khối lớp 10 của một trường trung học phổ thông có ba lớp 10A, 10B, 10C. Lớp 10A có 30 bạn, lớp 10B có 35 bạn, lớp 10C có 32 bạn. Nhà trường muốn chọn 4 bạn để thành lập đội cờ đỏ của khối sao cho có đủ đại diện của các lớp. Hỏi có bao nhiêu cách lựa chọn?
Phương pháp giải:
Chia 3 trường hợp:
- 2 bạn lớp 10A, 1 bạn lớp 10B, 1 bạn lớp 10C.
- 1 bạn lớp 10A, 2 bạn lớp 10B, 1 bạn lớp 10C.
- 1 bạn lớp 10A, 1 bạn lớp 10B, 2 bạn lớp 10C.
Áp dụng quy tắc nhân tính từng trường hợp có bao nhiêu cách chọn và quy tắc cộng để cộng 3 trường hợp với nhau.
Lời giải:
TH1: 2 bạn lớp 10A, 1 bạn lớp 10B, 1 bạn lớp 10C có số cách chọn là:
30. 29. 35. 32= 974 400 ( cách)
TH2: 1 bạn lớp 10A, 2 bạn lớp 10B, 1 bạn lớp 10C có số cách chọn là:
30. 35. 34. 32= 1 142 400 (cách)
TH3: 1 bạn lớp 10A, 1 bạn lớp 10B, 2 bạn lớp 10C có số cách chọn là:
30. 35. 32. 31= 1 041 600 (cách)
Vậy số cách lựa chọn là: 974 400 + 1 142 400 + 1 041 600= 3 158 400 cách
Bài tập
Bài 8.1 trang 65 SGK Toán 10 Tập 2: Trên giá sách có 8 cuốn truyện ngắn, 7 cuốn tiểu thuyết và 5 tập thơ (tất cả đều khác nhau). Vẽ sơ đồ hình cây cho biết bạn Phong có bao nhiêu cách chọn một cuốn để đọc vào ngày cuối tuần.
Phương pháp giải:
Áp dụng quy tắc cộng.
Lời giải:
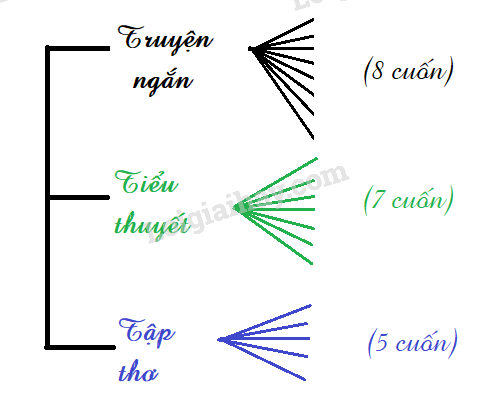
Bạn Phong có số cách chọn một cuốn để đọc vào ngày cuối tuần là:
8+ 7+ 5= 20 (cách)
Bài 8.2 trang 65 SGK Toán 10 Tập 2: Một người gieo đồng xu hai mặt, sau mỗi lần gieo thì ghi lại kết quả là sấp hay ngửa. Hỏi nếu người đó gieo 3 lần thì có thể có bao nhiêu khả năng xảy ra?
Phương pháp giải:
Áp dụng quy tắc nhân.
Lời giải:
Mỗi lần gieo có 2 khả năng xảy ra: xấp hoặc ngửa
Nếu người đó gieo 3 lần thì có thể có số khả năng xảy ra là:
2.2.2 = 8 (khả năng)
a) Sự tổ hợp giữa hai gen tạo ra mấy kiểu gen? Viết các kiểu gen đó.
b) Khi giao phối ngẫu nhiên, có bao nhiêu kiểu giao phối khác nhau từ các kiểu gen đó?
Lời giải:
a) Sự tổ hợp giữa hai gen tạo ra 3 kiểu gen: AA, aa, Aa.
b) Khi giao phối ngẫu nhiên, có số kiểu giao phối khác nhau từ các kiểu gen đó là: 3.3 = 9 ( kiểu)
Bài 8.4 trang 65 SGK Toán 10 Tập 2: Có bao nhiêu số tự nhiên
a) có 3 chữ số khác nhau
b) là số lẻ có 3 chữ số khác nhau?
c) là số có 3 chữ số và chia hết cho 5?
d) là số có 3 chữ số khác nhau và chia hết cho 5?
Phương pháp giải:
Áp dụng kết hợp quy tắc cộng và quy tắc nhân.
Lời giải:
Chọn các chữ số hàng trăm, hàng chục, hàng đơn vị trong các chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
a) - chữ số hàng trăm có 9 cách (khác 0)
- chữ số hàng chục có 9 cách (khác chữ số hàng trăm)
- chữ số hàng đơn vị có 8 cách (khác chữ số hàng trăm và hàng chục)
Vậy có tất cả 9. 9. 8= 648 số tự nhiên có 3 chữ số khác nhau.
b) - Chọn chữ số hàng đơn vị có 5 cách
- Chọn chữ số hàng trăm có 8 cách
- Chọn chữ số hàng chục có 8 cách
Vậy có tất cả 5. 8. 8= 320 số lẻ có 3 chữ số khác nhau.
c) - Chọn chữ số hàng đơn vị có 2 cách
- Chọn chữ số hàng trăm có 9 cách
- Chọn chữ số hàng chục có 10 cách
Vậy có tất cả 2.9.10= 180 số tự nhiên có 3 chữ số chia hết cho 5.
d) Trường hợp 1: chữ số hàng đơn vị là 0.
- Chọn chữ số hàng trăm có 9 cách
- Chọn chữ số hàng chục có 8 cách
Trường hợp 2 chữ số hàng đơn vị là 5:
- Chọn chữ số hàng trăm có 8 cách (khác 0 và 5)
- Chọn chữ số hàng chục có 8 cách
Vậy có tất cả 9.8 +8. 8= 136 số tự nhiên có 3 chữ số khác nhau và chia hết cho 5.
Bài 8.5 trang 65 SGK Toán 10 Tập 2: a) Mật khẩu của chương trình máy tính quy định gồm 3 kí tự, mỗi kí tự là một chữ số. Hỏi có thể tạo được bao nhiêu mật khẩu khác nhau?
b) Nếu chương trình máy tính quy định mới mật khẩu vẫn gồm 3 kí tự, nhưng kí tự đầu tiên phải là một chữ cái in hoa trong bảng chữ cái tiếng Anh gồm 26 chữ (từ A đến Z) và 2 kí tự sau là các chữ số (từ 0 đến 9). Hỏi quy định mới có thể tạo được nhiều hơn quy định cũ bao nhiêu mật khẩu khác nhau?
Lời giải:
a) Mỗi kí tự đều có 10 cách chọn.
Số mật khẩu có thể tạo ra là 10. 10. 10 = 1000
b) - Kí tự đầu có 26 cách chọn.
- 2 kí tự sau, mỗi kí tự có 10 cách chọn.
Quy định mới có thể tạo ra số mật khẩu là:
26. 10. 10= 2600
Quy định mới có thể tạo được nhiều hơn quy định cũ số mật khẩu khác nhau là:
2600- 1000= 1600 (mật khẩu)
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.