Toptailieu.vn xin giới thiệu 10 câu trắc nghiệm Quy tắc đếm Kết nối tri thức (có đáp án 2023) CHỌN LỌC, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
10 câu trắc nghiệm Quy tắc đếm Kết nối tri thức (có đáp án 2023) CHỌN LỌC
Lý thuyết
1. Quy tắc cộng
Quy tắc:
Có k phương án A1, A2, A3,..., Ak để thực hiện công việc. Trong đó:
- Có n1 cách thực hiện phương án A11,
- Có n2 cách thực hiện phương án A2
…
- Có nk cách thực hiện phương án Ak.
Khi đó, số cách để thực hiện công việc là: n1 + n2 + ... + nk cách.
2. Quy tắc nhân
Có k công đoạn A1, A2,..., Ak để thực hiện công việc.
- Có n1 cách thực hiện công đoạn A1.
- Có n2 cách thực hiện công đoạn A2.
…
- Có nk cách thực hiện công đoạn Ak.
Khi đó, số cách để thực hiện công việc là: n1 . n2 . ... nk cách.
Bài tập
Câu 1: Một lớp có 23 học sinh nữ và 17 học sinh nam.
a) Hỏi có bao nhiêu cách chọn một học sinh tham gia cuộc thi tìm hiểu môi trường?
A. 23 B. 17
C. 40 D. 391
b) Hỏi có bao nhiêu cách chọn hai học sinh tham gia hội trại với điều kiện có cả nam và nữ?
A. 40 B. 391
C. 780 D. 1560
Đáp án
a) Theo quy tắc cộng có: 23 +17 = 40 cách chọn một học sinh tham gia cuộc thi môi trường. Vì vậy chọn đáp án C
b) Việc chọn hai học sinh (nam và nữ) phải tiến hành hai hành động liên tiếp
Hành động 1: chọn 1 học sinh nữ trong số 23 học sinh nữ nên có 23 cách chọn
Hành động 2: chọn 1 học sinh nam nên có 17 cách chọn
Theo quy tắc nhân, có 23.17 = 391 cách chọn hai học sinh tham gia hội trại có cả nam và nữ. Vì vậy chọn phương án B
Câu 2: Một túi có 20 viên bi khác nhau trong đó có 7 bi đỏ, 8 bi xanh và 5 bi vàng
a) Số cách lấy 3 viên bi khác màu là
A. 20 B. 280
C. 6840 D. 1140
b) Số cách lấy 2 viên bi khác màu là:
A. 40 B. 78400
C. 131 D. 2340
Đáp án
a) Việc chọn 3 viên bi khác màu phải tiến hành 3 hành động liên tiếp: chọn 1 bi đỏ trong 7 bi đỏ nên có 7 cách chọn, tương tự có 8 cách chọn 1 bi xanh và 5 cách chọn 1 bi vàng. Theo quy tắc nhân ta có: 7.8.5 = 280 cách. Vậy đáp án là B
b) Muốn lấy được 2 viên bi khác màu từ trong túi đã cho xảy ra các trường hợp sau:
- Lấy 1 bi đỏ và 1 bi xanh: có 7 cách để lấy 1 bi đỏ và 8 cách để lấy 1 bi xanh. Do đó có 7.8 = 56 cách lấy
- Lấy 1 bi đỏ và 1 bi vàng: có 7 cách lấy 1 bi đỏ và 5 cách lấy 1 bi vàng. Do đó co 7.5 = 35 cách lấy
- Lấy 1 bi xanh và 1 bi vàng: có 8 cách để lấy 1 bi xanh và 5 cách để lấy 1 bi vàng. Do đó có 8.5 = 40 cách để lấy
- Áp dụng quy tắc cộng cho 3 trường hợp, ta có 56 + 35 + 40 = 131 cách
Vì vậy chọn đáp án là C
Câu 3: Từ các số 0,1,2,3,4,5 có thể lập được:
a) Bao nhiêu số có hai chữ số khác nhau và chia hết cho 5?
A. 25 B. 10
C. 9 D. 20
b) Bao nhiêu số có 3 chữ số khác nhau chia hết cho 3?
A. 36 B. 42
C. 82944 D. Một kết quả khác
c) Bao nhiêu số có ba chữ số (không nhất thiết khác nhau) và là số chẵn?
A. 60 B. 90
C. 450 D. 100
Đáp án
Gọi tập hợp E = {0,1,2,3,4,5}
a) Số tự nhiên có hai chữ số khác nhau có dạng:
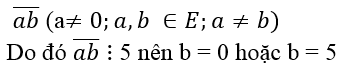
Với b = 0 thì có 5 cách chọn a ( vì a ≠ 0)
Với b = 5 thì có 4 cách chọn a ( vì a ≠ b và a ≠ 0)
Theo quy tắc cộng, có tất cả 5 + 4 = 9 số tự nhiên cần tìm. Chọn đáp án là C.
b) Số tự nhiên có ba chữ số khác nhau có dạng
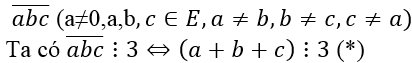
Trong E có các bộ chữ số thoả mãn (*) là:
(0,1,2);(0,1,5);(0,2,4);(1,2,3);(1,3,5);(2,3,4);(3,4,5)
Mỗi bộ gồm ba chữ số khác nhau và khác 0 nên ta viết được 3.2.1 = 6 số có ba chữ số chia hết cho 3
Mỗi bộ gồm ba chữ số khác nhau và có một chữ số 0 nên ta viết được 2.2.1 = 4 số có ba chữ số chia hết cho 3
Vậy theo quy tắc cộng ta có: 6.4 + 4.3 = 36 số có 3 chữ số chia hết cho 3
Chọn đáp án là A
c) Số tự nhiên có 3 chữ số có dạng
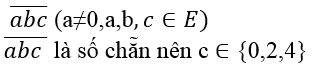
Có ba cách chọn chữ số c ( vì c ∈ {0,2,4}).
Ứng với mỗi cách chọn c , có 6 cách chọn chữ số b (vì b ∈ E)
Ứng với mỗi cách chọn c, b có 5 cách chọn chữ số a (vì a ∈ E và a≠ 0)
Áp dụng quy tắc nhân ta có 3.6.5 = 90 số có 3 chữ số. Vì vậy đáp án là B
Câu 4: Giả sử bạn muốn mua một áo sơ mi size S hoặc size M. Áo size S có 5 màu khác nhau, áo size M có 4 màu khác nhau. Hỏi có bao nhiêu sự lựa chọn (về màu áo và cỡ áo)?
A. 9
B. 5
C. 4
D. 20
Đáp án
Nếu chọn áo size S thì sẽ có 5 cách.
Nếu chọn áo size M thì sẽ có 4 cách.
Theo qui tắc cộng, ta có 5+ 4= 9 cách chọn mua áo.
Chọn đáp án A
Câu 5: Một người có 4 cái quần khác nhau, 6 cái áo khác nhau, 3 chiếc cà vạt khác nhau. Để chọn một cái quần hoặc một cái áo hoặc một cái cà vạt thì số cách chọn khác nhau là:
A.13
B. 72
C. 12
D. 30
Đáp án
Nếu chọn một cái quần thì sẽ có 4 cách.
Nếu chọn một cái áo thì sẽ có 6 cách.
Nếu chọn một cái cà vạt thì sẽ có 3 cách.
Theo qui tắc cộng, ta có 4 + 6 + 3 = 13 cách chọn.
Chọn đáp án A
Câu 6: Trong một trường THPT, khối 11 có 280 học sinh nam và 325 học sinh nữ. Nhà trường cần chọn một học sinh ở khối 11 đi dự dạ hội của học sinh thành phố. Hỏi nhà trường có bao nhiêu cách chọn?
A. 280
B. 325
C. 45
D. 605
Đáp án
Nếu chọn một học sinh nam có 280 cách.
Nếu chọn một học sinh nữ có 325 cách.
Theo qui tắc cộng, ta có 280 + 325 = 605 cách chọn.
Chọn đáp án D
Câu 7: Trong một hộp chứa sáu quả cầu trắng được đánh số từ 1 đến 6 và ba quả cầu đen được đánh số 7, 8, 9. Có bao nhiêu cách chọn một trong các quả cầu ấy?
A. 27
B. 9
C. 6
D.3
Đáp án
Vì các quả cầu trắng hoặc đen đều được đánh số phân biệt nên mỗi lần lấy ra một quả cầu bất kì là một lần chọn.
Nếu chọn một quả trắng có 6 cách.
Nếu chọn một quả đen có 3 cách.
Theo qui tắc cộng, ta có 6 + 3 = 9 cách chọn.
Chọn đáp án B
Câu 8: Giả sử từ tỉnh A đến tỉnh B có thể đi bằng các phương tiện: ô tô, tàu hỏa, tàu thủy hoặc máy bay. Mỗi ngày có 10 chuyến ô tô, 5 chuyến tàu hỏa, 3 chuyến tàu thủy và 2 chuyến máy bay. Hỏi có bao nhiêu cách đi từ tỉnh A đến tỉnh B?
A.20
B. 300
C. 18
D. 15
Đáp án
Nếu đi bằng ô tô có 10 cách.
Nếu đi bằng tàu hỏa có 5 cách.
Nếu đi bằng tàu thủy có 3 cách.
Nếu đi bằng máy bay có 2 cách.
Theo qui tắc cộng, ta có 10 + 5+ 3+ 2= 20 cách chọn.
Chọn đáp án A
Câu 9: Có 3 kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và 4 kiểu dây (kim loại, da, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
A. 4
B. 7
C.12
D. 24
Đáp án
Để chọn một chiếc đồng hồ, ta có:
Có 3 cách chọn mặt.
Có 4 cách chọn dây.
Vậy theo qui tắc nhân ta có:3.4 = 12 cách.
Chọn đáp án C
Câu 10: Một người có 4 cái quần, 6 cái áo, 3 chiếc cà vạt. Để chọn mỗi thứ một món thì có bao nhiều cách chọn bộ quần-áo-cà vạt khác nhau?
A. 13.
B. 72.
C. 12.
D. 30.
Đáp án
Để chọn một bộ quần-áo-cà vạt , ta có:
Có 4 cách chọn quần.
Có 6 cách chọn áo.
Có 3 cách chọn cà vạt.
Vậy theo qui tắc nhân ta có : 4.6.3 = 72 cách.
Chọn đáp án B
Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.