Toptailieu.vn xin giới thiệu 05 câu trắc nghiệm Bài tập cuối chương 8 Kết nối tri thức (có đáp án 2023) CHỌN LỌC, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
05 câu trắc nghiệm Bài tập cuối chương 8 Kết nối tri thức (có đáp án 2023) CHỌN LỌC
Lý thuyết
I. Quy tắc đếm
1. Quy tắc cộng
Quy tắc:
Có k phương án A1, A2, A3,..., Ak để thực hiện công việc. Trong đó:
- Có n1 cách thực hiện phương án A11,
- Có n2 cách thực hiện phương án A2
…
- Có nk cách thực hiện phương án Ak.
Khi đó, số cách để thực hiện công việc là: n1 + n2 + ... + nk cách.
2. Quy tắc nhân
Có k công đoạn A1, A2,..., Ak để thực hiện công việc.
- Có n1 cách thực hiện công đoạn A1.
- Có n2 cách thực hiện công đoạn A2.
…
- Có nk cách thực hiện công đoạn Ak.
Khi đó, số cách để thực hiện công việc là: n1 . n2 . ... nk cách.
II. Hoán vị, chỉnh hợp và tổ hợp
1. Hoán vị
Cho n phần tử khác nhau (n ≥ 1). Mỗi cách sắp thứ tự của n phần tử đã cho, mà trong đó mỗi phần tử có mặt đúng một lần, được gọi là một hoán vị của n phần tử đó.
Định lí
Số các hoán vị của n phần tử khác nhau đã cho (n ≥ 1) được kí hiệu là Pn và bằng:
Pn = n(n - 1)(n - 2) ... 2.1 = n!
2. Chỉnh hợp
Định nghĩa
Cho tập hợp A gồm n phần tử (n ≥ 1).
Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
Chú ý
Mỗi hoán vị của n phần tử khác nhau đã cho chính là một chỉnh hợp chập n của n phần tử đó.
Định lí
Số chỉnh hợp chập k của n phần tử khác nhau đã cho được kí hiệu là ![]() và bằng
và bằng
![]()
Với quy ước 0! = 1.
3. Tổ hợp
Định nghĩa
Cho n phần tử khác nhau (n ≥ 1). Mỗi tập con gồm k phần tử khác nhau (không phân biệt thứ tự) của tập hợp n phần tử đã cho (0 ≤ k ≤ n) được gọi là một tổ hợp chập k của n phần tử đã cho (với quy ước tổ hợp chập 0 của n phần tử bất kỳ là tập rỗng).
Định lí
Số các tổ hợp chập k của n phần tử khác nhau đã cho được kí hiệu là ![]() và bằng
và bằng
![]() Định lí
Định lí
Với mọi n ≥ 1; 0 ≤ k ≤ n, ta có:
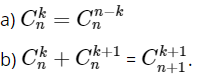
4. Một số dạng toán thường gặp
Dạng 1: Giải phương trình, hệ phương trình hoán vị, chỉnh hợp, tổ hợp
Phương pháp chung:
- Sử dụng các công thức tính số hoán vị, chỉnh hợp, tổ hợp để biến đổi phương trình.
- Kiểm tra điều kiện của nghiệm và kết luận.
Dạng 2: Giải bất phương trình hoán vị, chỉnh hợp, tổ hợp
Phương pháp chung:
- Sử dụng các công thức tính số hoán vị, chỉnh hợp, tổ hợp để biến đổi bất phương trình.
- Kiểm tra điều kiện của nghiệm và kết luận.
III. Nhị thức Newton
1. Công thức nhị thức Niu - Tơn
1.1. Công thức nhị thức Niu - Tơn
Với a, b là những số thực tùy ý và với mọi số tự nhiên n ≥ 1, ta có:
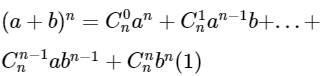
1.2. Quy ước
Với a là số thực khác 0 và n là số tự nhiên khác 0, ta quy ước:
![]()
1.3. Chú ý
Với các điều kiện và quy ước ở trên, đồng thời thêm điều kiện a và b đều khác 0, có thể viết công thức (1) ở dạng sau đây:
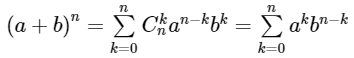 2. Tam giác Pa-xcan
2. Tam giác Pa-xcan
2.1. Tam giác Pa-xcan là tam giác số ghi trong bảng

2.2. Cấu tạo của tam giác Pa-xcan
- Các số ở đầu và cuối hàng đều bằng 1.
- Xét hai số ở cột k và cột k + 1, đồng thời cùng thuộc dòng n, (k ≥ 0; n ≥ 1), ta có: tổng của hai số này bằng số đứng ở giao của cột k + 1 và dòng n + 1.
2.3. Tính chất của tam giác Pa-xcan
Từ cấu tạo của tam giác Pa-xcan, có thể chứng minh được rằng:
a) Giao của dòng n và cột k là ![]()
b) Các số của tam giác Pa-xcan thỏa mãn công thức Pa-xcan:
![]()
c) Các số ở dòng n là các hệ số trong khai triển của nhị thức (a + b)n (theo công thức nhị thức Niu - Tơn), với a, b là hai số thực tùy ý.
Chẳng hạn, các số ở dòng 4 là các hệ số trong khai triển của (a + b)4 (theo công thức nhị thức Niu - Tơn) dưới đây:
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
Bài tập
Câu 1: Số cách cắm 4 bông hoa khác nhau vào 4 bình hoa khác nhau (mỗi bông hoa cắm vào một bình) là
A. 16.
B. 24.
C. 8.
D. 4.
Lời giải:
Đáp án đúng là: B.
Mỗi cách cắm 4 bông hoa vào 4 bình hoa khác nhau (mỗi bông hoa cắm vào một bình) là một hoán vị của 4 phần tử.
Vậy có P4 = 4! = 24 cách cắm hoa thỏa mãn yêu cầu bài toán.
Câu 2: Số các số có ba chữ số khác nhau, trong đó các chữ số đều lớn hơn 0 và nhỏ hơn hoặc bằng 5 là
A. 120.
B. 60.
C. 720.
D. 2.
Lời giải:
Đáp án đúng là: B.
Các chữ số lớn hơn 0 và nhỏ hơn hoặc bằng 5 là: 1, 2, 3, 4, 5.
Ta cần lập các số có 3 chữ số khác nhau từ 5 chữ số: 1, 2, 3, 4, 5.
Mỗi cách lập một số thỏa mãn yêu cầu là một chỉnh hợp chập 3 của 5 phần tử.
Vậy ta lập được ![]() = 60
= 60
Câu 3: Số cách chọn 3 bạn học sinh đi học bơi từ một nhóm 10 bạn học sinh là
A. 3 628 800.
B. 604 800.
C. 120.
D. 720.
Lời giải:
Đáp án đúng là: C.
Mỗi cách chọn 3 học sinh đi học bơi từ nhóm 10 bạn học sinh là một tổ hợp chập 3 của 10 phần tử.
Vậy có ![]() = 120 cách chọn.
= 120 cách chọn.
Câu 4: Bạn An gieo một con xúc xắc hai lần. Số các trường hợp để tổng số chấm xuất hiện trên con xúc xắc bằng 8 qua hai lần gieo là
A. 36.
B. 6.
C. 5.
D. 4.
Lời giải:
Đáp án đúng là: C.
Một con xúc xắc có 6 mặt, các mặt được đánh dấu từ 1 chấm đến 6 chấm.
Gieo một con xúc xắc thì có 6 khả năng xảy ra: xuất hiện mặt 1 chấm, 2 chấm, 3 chấm, 4 chấm, 5 chấm hoặc 6 chấm.
Ta có: 2 + 6 = 6 + 2 = 8; 3 + 5 = 5 + 3 = 8; 4 + 4 = 8.
Gieo con xúc xắc 2 lần để tổng số chấm xuất hiện là 8 thì:
+ Gieo lần 1 xuất hiện mặt 2 chấm, lần 2 xuất hiện mặt 6 chấm.
+ Gieo lần 1 xuất hiện mặt 6 chấm, lần 2 xuất hiện mặt 2 chấm.
+ Gieo lần 1 xuất hiện mặt 3 chấm, lần 2 xuất hiện mặt 5 chấm.
+ Gieo lần 1 xuất hiện mặt 5 chấm, lần 2 xuất hiện mặt 3 chấm.
+ Gieo lần 1 xuất hiện mặt 4 chấm, lần 2 xuất hiện mặt 4 chấm.
Do đó, có 5 khả năng có thể xảy ra.
Vậy có 5 trường hợp gieo thỏa mãn.
Câu 5: Hệ số của x4 trong khai triển nhị thức (3x – 4)5 là
A. 1 620.
B. 60.
C. – 60.
D. – 1 620.
Lời giải:
Đáp án đúng là: D.
Số hạng chứa x4 trong khai triển của (3x – 4)5 là: 5 . (3x)4 . (– 4) = – 1 620x4.
Vậy hệ số của x4 trong khai triển (3x – 4)5 là – 1 620.
Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 26: Biến cố và định nghĩa cổ điển của xác suất
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.