Toptailieu.vn xin giới thiệu 14 câu trắc nghiệm Nhị thức Newton Kết nối tri thức (có đáp án 2023) CHỌN LỌC, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
14 câu trắc nghiệm Nhị thức Newton Kết nối tri thức (có đáp án 2023) CHỌN LỌC
Lý thuyết
I. Công thức nhị thức Niu - Tơn
1. Công thức nhị thức Niu - Tơn
Với a, b là những số thực tùy ý và với mọi số tự nhiên n ≥ 1, ta có:
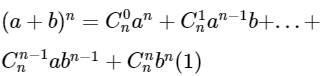
2. Quy ước
Với a là số thực khác 0 và n là số tự nhiên khác 0, ta quy ước:
3. Chú ý
Với các điều kiện và quy ước ở trên, đồng thời thêm điều kiện a và b đều khác 0, có thể viết công thức (1) ở dạng sau đây:
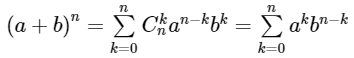II. Tam giác Pa-xcan
1. Tam giác Pa-xcan là tam giác số ghi trong bảng
2. Cấu tạo của tam giác Pa-xcan
- Các số ở đầu và cuối hàng đều bằng 1.
- Xét hai số ở cột k và cột k + 1, đồng thời cùng thuộc dòng n, (k ≥ 0; n ≥ 1), ta có: tổng của hai số này bằng số đứng ở giao của cột k + 1 và dòng n + 1.
3. Tính chất của tam giác Pa-xcan
Từ cấu tạo của tam giác Pa-xcan, có thể chứng minh được rằng:
a) Giao của dòng n và cột k là 
b) Các số của tam giác Pa-xcan thỏa mãn công thức Pa-xcan:
c) Các số ở dòng n là các hệ số trong khai triển của nhị thức (a + b)n (theo công thức nhị thức Niu - Tơn), với a, b là hai số thực tùy ý.
Chẳng hạn, các số ở dòng 4 là các hệ số trong khai triển của (a + b)4 (theo công thức nhị thức Niu - Tơn) dưới đây:
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
Bài tập
Câu 1: Khai triển biểu thức (x-m2)4 thành tổng các đơn thức:
A. x4 –x3m+x2m2 + m4
B. x4 –x3m2+x2m4 –xm6+ m8
C. x4 –4x3m+6x2m2 -4xm+ m4
D. x4 –4x3m2+6x2m4 – 4xm6+ m8
Đáp án
Sử dụng nhị thức Niuton với a = x, b = - m2
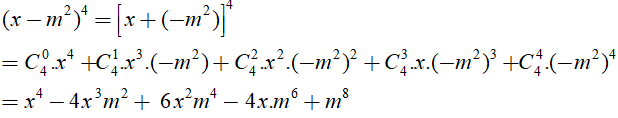
Chọn đáp án D
Câu 2: Tìm số hạng không chứa x trong khai triển
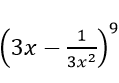
A. 2268 B. -2268
C. 84 D. -27
Đáp án
Chọn đáp án là B
Câu 3: Xác định hệ số của số hạng chứa x3 trong khai triển (x2-2/x)n nếu biết tổng các hệ số của ba số hạng đầu trong khai triển đó bằng 49.
A. 160 B. -160
C. 160x3 D. -160x3
Đáp án
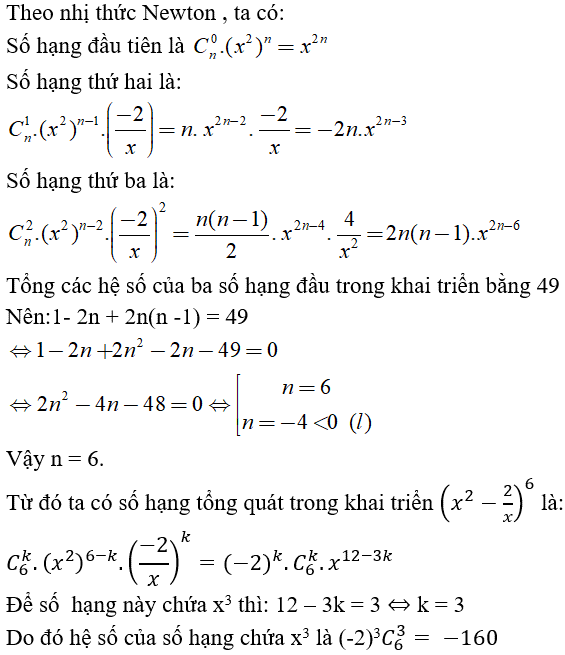
Chọn đáp án là B
Câu 4: Tính tổng S = 32015.C2015o-32014C20151+32013C20152-…+3C20152014 -C20152015
A. 22015 B. -22015
C. 32015 D. 42015
Đáp án
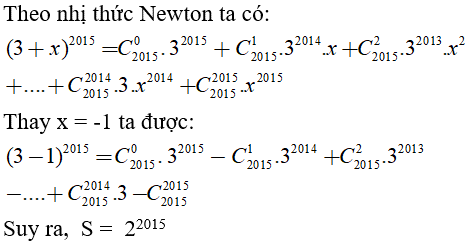
Chọn đáp án A
Câu 5: Trong khai triển nhị thức (a + 2)n + 6, (n ∈ N). Có tất cả 17 số hạng. Vậy n bằng:
A. 17
B. 11
C. 10
D. 12
Đáp án
Trong khai triển (a + 2)n+6, (n ∈ N)
Có tất cả n+6 + 1 = n +7 số hạng.
Do đó n + 7 = 17 ⇔ n = 10.
Chọn đáp án C
Câu 6: Tìm hệ số của x12 trong khai triển (2x - x2)10
Đáp án
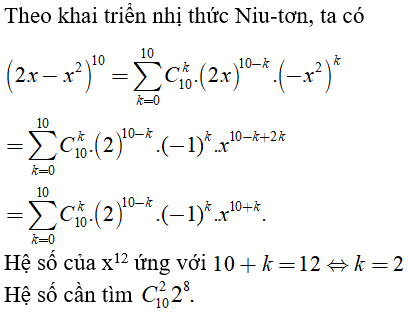
Chọn đáp án B
Câu 7: Tìm số hạng chứa x3 trong khai triển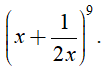 
Đáp án
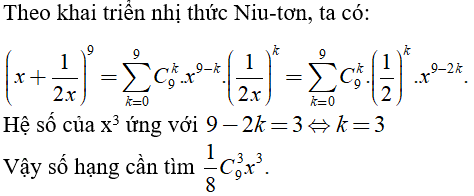
Chọn đáp án B
Câu 8: Tìm số hạng đứng giữa trong khai triển (x3 + xy)21
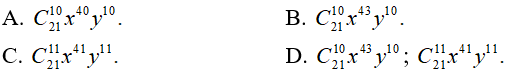
Đáp án
Theo khai triển nhị thức Niu-tơn, ta có
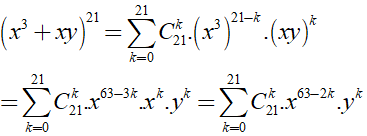
Suy ra khai triển (x3 + xy)21 có 22 số hạng nên có hai số hạng đứng giữa là số hạng thứ 11 (ứng với k = 10) và số hạng thứ 12 (ứng với k = 11). Vậy hai số hạng đứng giữa cần tìm là
.
Chọn đáp án D
Câu 9: Tìm hệ số của x5 trong khai triển P(x) = x(1 - 2x)5 + x2(1 + 3x)10
A. 80
B. 3240
C. 3320
D. 259200
Đáp án
Chọn đáp án C
Câu 10: Tìm hệ số của x5 trong khai triển : P(x) = (1 + x) + 2(1 + x)2 + ... + 8(1 + x)8.
A. 630
B. 635
C. 636
D.637
Đáp án
Các biểu thức (1 + x), (1 + x)2, ⋯, (1 + x)4 không chứa số hạng chứa x5.
Chọn đáp án C
Câu 11: Tìm số nguyên dương n thỏa mãn
.
A.n = 8
B.n = 9
C.n = 10
D. n = 11
Đáp án
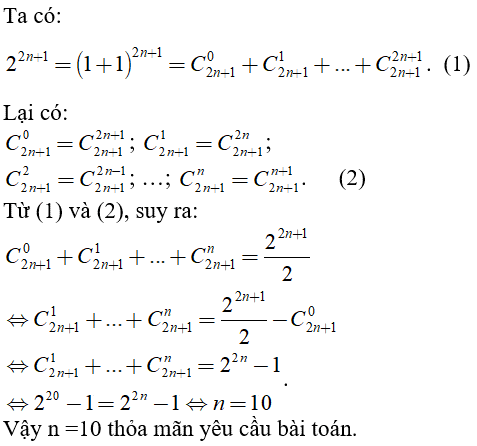
Chọn đáp án C
Câu 12: Tìm số nguyên dương n thỏa mãn 
.
A.n = 5
B.n = 9
C.n = 10
D.n = 4
Đáp án
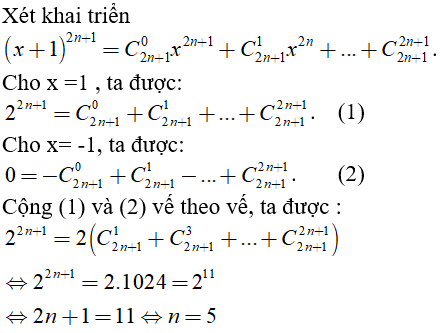
Chọn đáp án A
Câu 13: Tìm số nguyên dương n sao cho:
A. 5
B. 11
C. 12
D. 4
Đáp án
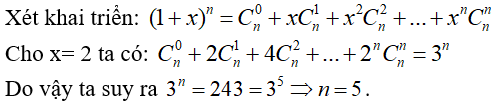
Chọn đáp án A
Câu 14: Tính 
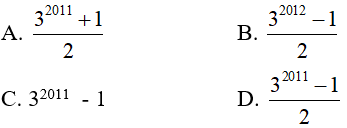
Đáp án
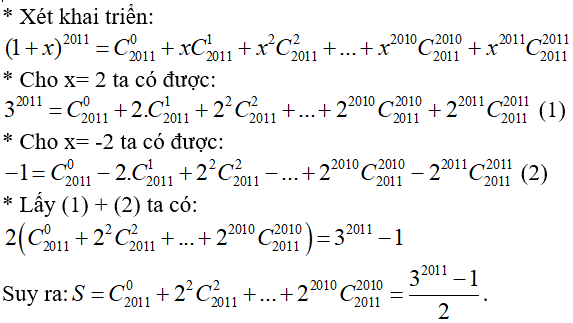
Chọn đáp án D
Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 24: Hoán vị, chỉnh hợp và tổ hợp
Bài 26: Biến cố và định nghĩa cổ điển của xác suất
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
