Toptailieu.vn xin giới thiệu 12 câu trắc nghiệm Hoán vị, chỉnh hợp và tổ hợp Kết nối tri thức (có đáp án 2023) CHỌN LỌC, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
12 câu trắc nghiệm Hoán vị, chỉnh hợp và tổ hợp Kết nối tri thức (có đáp án 2023) CHỌN LỌC
Lý thuyết
1. Hoán vị
Cho n phần tử khác nhau (n ≥ 1). Mỗi cách sắp thứ tự của n phần tử đã cho, mà trong đó mỗi phần tử có mặt đúng một lần, được gọi là một hoán vị của n phần tử đó.
Định lí
Số các hoán vị của n phần tử khác nhau đã cho (n ≥ 1) được kí hiệu là Pn và bằng:
Pn = n(n - 1)(n - 2) ... 2.1 = n!
2. Chỉnh hợp
Định nghĩa
Cho tập hợp A gồm n phần tử (n ≥ 1).
Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
Chú ý
Mỗi hoán vị của n phần tử khác nhau đã cho chính là một chỉnh hợp chập n của n phần tử đó.
Định lí
Số chỉnh hợp chập k của n phần tử khác nhau đã cho được kí hiệu là ![]() và bằng
và bằng
![]()
Với quy ước 0! = 1.
3. Tổ hợp
Định nghĩa
Cho n phần tử khác nhau (n ≥ 1). Mỗi tập con gồm k phần tử khác nhau (không phân biệt thứ tự) của tập hợp n phần tử đã cho (0 ≤ k ≤ n) được gọi là một tổ hợp chập k của n phần tử đã cho (với quy ước tổ hợp chập 0 của n phần tử bất kỳ là tập rỗng).
Định lí
Số các tổ hợp chập k của n phần tử khác nhau đã cho được kí hiệu là ![]() và bằng
và bằng
![]() Định lí
Định lí
Với mọi n ≥ 1; 0 ≤ k ≤ n, ta có:
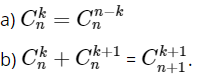
4. Một số dạng toán thường gặp
Dạng 1: Giải phương trình, hệ phương trình hoán vị, chỉnh hợp, tổ hợp
Phương pháp chung:
- Sử dụng các công thức tính số hoán vị, chỉnh hợp, tổ hợp để biến đổi phương trình.
- Kiểm tra điều kiện của nghiệm và kết luận.
Dạng 2: Giải bất phương trình hoán vị, chỉnh hợp, tổ hợp
Phương pháp chung:
- Sử dụng các công thức tính số hoán vị, chỉnh hợp, tổ hợp để biến đổi bất phương trình.
- Kiểm tra điều kiện của nghiệm và kết luận.
Bài tập
Câu 1: Một tổ có 4 học sinh nam và 5 học sinh nữ
a) Hỏi có bao nhiêu cách xếp học sinh trong tổ thành một hàng dọc?
A. 4!.5! B. 4!+5!
C. 9! D. A49.A59
b) Hỏi có bao nhiêu cách xếp học sinh trong tổ thành hàng dọc sao cho học sinh nam và nữ đúng xen kẽ nhau?
A. 4!.5! B. 4!+5!
C. 9! D. A49.A59
Đáp án
- Mỗi cách xếp có 4 + 5 = 9 học sinh thành hàng dọc là một hoán vị của 9 học sinh đó. Vậy có tất cả 9! cách xếp. Chọn đáp án là C
Nhận xét: học sinh có thể nhầm lẫn xếp nam và nữ riêng nên cho kết quả 4!.5! (phương án A); hoặc vừa xếp nam và nữ riêng và sử dụng quy tắc cộng để cho kết quả 4!+5! (phương án B); hoặc chọn 4 học sinh nam trong 9 học sinh và 5 học sinh nữ trong 9 học sinh để cho kết quả D. A49.A95 ( phương án D)
b) Do số học sinh nữ nhiều hơn số học sinh nam là 1 bạn nên để nam, nữ đứng xen kẽ thì nữ đứng trước.
- Nếu đánh số theo hàng dọc từ 1 đến 9 thì cần xếp 5 học nữ vào 5 vị trí lẻ nên có 5!cách xếp; và xếp 4 học sinh nam vào 4 vị trí chẵn nên có 4!cách xếp. Theo quy tắc nhân ta có, ta có 4!.5! Cách xếp 9 học sinh thành hàng dọc xen kẽ nam nữ.
Câu 2:
a) Từ tập A = {1; 2; 3; 4; 5; 6; 7; 8; 9}, lập được bao nhiêu số có bốn chữ số khác nhau?
A. 4! B. A94
C. 9A93 D. C94
b) Có bao nhiêu số có bốn chữ số khác nhau?
A. 4! B. 9A93
C. 9C93 D. Một đáp án khác
Đáp án
a) Mỗi số tự nhiên có bốn chữ số khác nhau được tạo ra từ các chữ số của tập A là một chỉnh hợp chập 4 của 9 phần tử.
Vậy có A94 số cần tìm. Chọn đáp án B
Nhận xét: học sinh có thể nhầm coi mỗi số có bốn chữ số là một hoán vị của 4 phần tử nên chọn kết quả là 4! (phương án A); hoặc là một tổ hợp tập 4 của 9 phần tử nên chọn kết quả C94 (phương án D); hoặc suy luận có 9 cách chọn chữ số hàng nghìn và có C93 cách chọn 3 chữ số còn lại nên có kết quả 9C93 (phương án C)
b) Gọi số có bốn chữ số khác nhau là
![]()
Do a ∈ {1,2,3,4,5,6,7,8,9} nên có 9 cách chọn a.
Ứng với mỗi cách chọn a, còn 10 - 1 = 9 chữ số để viết
![]()
(b, c, d có thể bằng 0), mỗi cách viết
![]()
là một chỉnh hợp chập 3 của 9 chữ số, nên có A93 số
![]()
Theo quy tắc nhân, có 9A93 số cần tìm. Chọn đáp án là B.
Câu 3: Trong mặt phẳng có 18 điểm phân biệt trong đó không có ba điểm nào thẳng hàng
a) Số tam giác mà các đỉnh của nó thuộc tập hợp các điểm đã cho là:
A. A183 B. C183
C. 6 D. 18!/3
b) Số vecto có điểm đầu và điểm cuối thuộc tập điểm đã cho là:
A. A182 B. C182
C. 6 D. 18!/2
Đáp án
- Chọn 3 điểm trong 18 điểm đã cho làm 3 đỉnh của một tam giác. Mỗi tam giác là một tổ hợp chập 3 của 18. Vì vậy số tam giác là C183 (chọn phương án B)
Nhận xét: học sinh có thể nhầm cho rằng mỗi tam giác là một chỉnh hợp chập 3 của 18, nên số tam giác là A183 (phương án A); hoặc suy luận một tam giác có 3 đỉnh nên 18 điểm cho ta 18/3 = 6 tam giác (phương án C); hoặc suy luận 18 điểm có 18! cách và mỗi tam giác có 3 đỉnh nên số tam giác là 18!/3 cách (phương án D)
- Do
![]()
Nên mỗi vecto là một chỉnh hợp chập hai của 18.
Vì vậy, số vecto là A182
Chọn đáp án A
Câu 4: Có 5 bì thư khác nhau và có 8 con tem khác nhau. Chọn từ đó ra 3 bì thư và 3 con tem sau đó dán 3 con tem lên 3 bì thư đã chọn. Biết rằng một bì thư chỉ dán 1 con tem. Hỏi có bao nhiêu cách dán?
A. A53.A83 B. 3!A53 A83
C. C53.C83 D. 3!C53.C83
Đáp án
Có 5 bì thư khác nhau, chọn 3 bì thư có C53 cách chọn
Có 8 tem khác nhau, chọn 3 con tem thì có C83 cách chọn
Dán 3 con tem lên 3 bì thư thì có 3!cách dán khác nhau. Theo quy tắc nhân ta có 3!C53.C83 cách dán 3 con tem lên 3 bì thư
Chọn đáp án D
Nhận xét: học sinh có thể nhầm lẫn: số cách chọn 3 bì thư là A53, số cách chọn 3 con tem là A83 hoặc không tính cách dán 3 con tem lên 3 bì thư dẫn đến có thể chọn các phương án A, B và C.
Câu 5: Giải phương trình Ax3+Cxx-3=14x (x là ẩn số)
A. x= 5 và x= -2 B. x = 5
C. x= -2 D. vô nghiệm
Đáp án
Điều kiện x ∈ N và x ≥ 3, ta có:
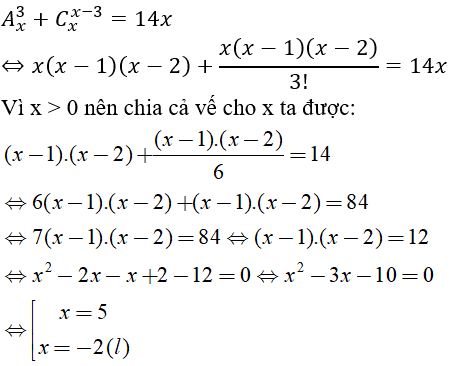
Chọn đáp án B
Câu 6: Sắp xếp năm bạn học sinh An, Bình, Chi, Dũng, Lệ vào một chiếc ghế dài có 5 chỗ ngồi. Số cách sắp xếp sao cho bạn Chi luôn ngồi chính giữa là
A. 24
B. 120
C. 60
D. 16
Đáp án
Xếp bạn Chi ngồi giữa có 1 cách.
Số cách xếp 4 bạn sinh An, Bình, Dũng, Lệ vào 4 chỗ còn lại là một hoán vị của 4 phần tử nên có có 4! = 24 cách.
Vậy có 1.24 = 24 cách xếp.
Chọn đáp án A
Câu 7: Có 3 viên bi đen khác nhau, 4 viên bi đỏ khác nhau, 5 viên bi xanh khác nhau. Hỏi có bao nhiêu cách sắp xếp các viên bi trên thành một dãy sao cho các viên bi cùng màu ở cạnh nhau?
A. 345600
B. 725760
C.103680
D.518400
Đáp án
Số các hoán vị về màu bi khi xếp thành dãy là 3!
Số cách xếp 3 viên bi đen khác nhau thành dãy là 3!
Số cách xếp 4 viên bi đỏ khác nhau thành dãy là 4!
Số cách xếp 5 viên bi xanh khác nhau thành dãy là 5!
⇒ Số cách xếp các viên bi trên thành một dãy sao cho các viên bi cùng màu ở cạnh nhau là 3!. 3!. 4!. 5! = 103680 cách.
Chọn đáp án C
Câu 8: Có bao nhiêu cách xếp khác nhau cho 4 người ngồi vào 6 chỗ trên một bàn dài?
A.15
B. 720
C. 30
D. 360
Đáp án
Số cách xếp khác nhau cho 4 người ngồi vào 6 chỗ trên một bàn dài là một chỉnh hợp chập 4 của 6 phần tử.
Suy ra có ![]() cách.
cách.
Chọn đáp án D
Câu 9: Trong một ban chấp hành đoàn gồm 7 người, cần chọn ra 3 người vào ban thường vụ. Nếu cần chọn ban thường vụ gồm ba chức vụ bí thư, phó bí thư, ủy viên thường vụ thì có bao nhiêu cách chọn?
A. 210
B. 200
C. 180
D. 150
Đáp án
Số cách chọn ban thường vụ gồm ba chức vụ bí thư, phó bí thư, ủy viên thường vụ từ 7 người là số các chỉnh hợp chập ba của bảy phần tử.
Vậy có ![]() .
.
Chọn đáp án A
Câu 10: Một lớp học có 40 học sinh gồm 25 nam và 15 nữ. Chọn 3 học sinh để tham gia vệ sinh công cộng toàn trường, hỏi có bao nhiêu cách chọn như trên?
A.9880
B. 59280
C. 2300
D. 455
Đáp án
Nhóm học sinh 3 người được chọn (không phân biệt nam, nữ - công việc) là một tổ hợp chập 3 của 40 (học sinh).
Vì vậy, số cách chọn nhóm học sinh là 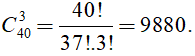
Chọn đáp án A
Câu 11: Có bao nhiêu cách cắm 3 bông hoa giống nhau vào 5 lọ khác nhau (mỗi lọ cắm không quá một bông)?
A. 10
B. 30
C. 6
D. 60
Đáp án
Cắm 3 bông hoa giống nhau, mỗi bông vào 1 lọ nên ta sẽ lấy 3 lọ bất kỳ trong 5 lọ khác nhau để cắm bông.
Vậy số cách cắm bông chính là một tổ hợp chập 3 của 5 phần tử (lọ hoa).
Như vậy, ta có 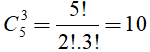 cách.
cách.
Chọn đáp án A
Câu 12: Trong mặt phẳng, cho 6 điểm phân biệt sao cho không có ba điểm nào thẳng hàng. Hỏi có thể lập được bao nhiêu tam giác mà các đỉnh của nó thuộc tập điểm đã cho?
A. 15
B. 20
C. 60
D. Một số khác.
Đáp án
Cứ 3 điểm phân biệt không thẳng hàng tạo thành một tam giác.
Lấy 3 điểm bất kỳ trong 6 điểm phân biệt thì số tam giác cần tìm chính là một tổ hợp chập 3 của 6 phần tử (điểm).
Như vậy, ta có ![]() tam giác.
tam giác.
Chọn đáp án B
Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.