Lý thuyết

1. Mệnh đề là câu khẳng định có thể xác định được tính đúng hay sai của nó. Một mệnh đề không thể vừa đúng, vừa sai.

2. Mệnh đề chứa biến là câu khẳng định mà sự đúng hay sai của nó còn tùy thuộc vào một hay nhiều yếu tố biến đổi.

Ví dụ: Câu "Số nguyên n chia hết cho 3" không phải là mệnh đề, vì không thể xác định được nó đúng hay sai.

Nếu ta gán cho n giá trị n = 4 thì ta có thể có một mệnh đề sai.

Nếu gán cho n giá trị n = 9 thì ta có một mệnh đề đúng.

3. Phủ định của một mệnh đề A, là một mệnh đề, kí hiệu là . Hai mệnh đề A và  là hai câu khẳng định trái ngược nhau.

Nếu A đúng thì  sai.

Nếu A sai thì  đúng.

Ví dụ: Cho mệnh đề A: "5 là số nguyên tố".

Đây là mệnh đề đúng.

Mệnh đề phủ định: "5 không là số nguyên tố"

Đây là mệnh đề sai.

4. Mệnh đề kéo theo

Mệnh đề kéo theo có dạng: "Nếu A thì B", trong đó A và B là hai mệnh đề. Mệnh đề "Nếu A thì B" kí hiệu là A ⇒ B. Tính đúng, sai của mệnh đề kéo theo như sau:

Mệnh đề A ⇒ B chỉ sai khi A đúng và B sai.

Ví dụ: Cho hai mệnh đề A:"3 chia hết cho 2" và B:"4 là số chẵn"

Khi đó A ⇒ B phát biểu là: "Nếu 3 chia hết cho 2 thì 4 là số chẵn"

Đây là mệnh đề đúng vì A sai, B đúng. (Mệnh đề A sai nhưng không ảnh hướng đến tính đúng của mệnh đề B nên mệnh đề kéo theo vẫn đúng).

5. Mệnh đề đảo

Mệnh đề "B ⇒ A" là mệnh đề đảo của mệnh đề A ⇒ B. Mệnh đề này chỉ sai khi B đúng, A sai.

Ví dụ: Trong ví dụ trên, mệnh đề B ⇒ A phát biểu là: "Nếu 4 là số chẵn thì 3 chia hết cho 2"

Mệnh đề này sai vì B đúng, A sai.

6. Mệnh đề tương đương

Nếu A ⇒ B là một mệnh đề đúng và mệnh đề B ⇒ A cũng là một mệnh đề đúng thì ta nói A tương đương với B, kí hiệu: A ⇔ B.

Khi A ⇔ B, ta cũng nói A là điều kiện cần và đủ để có B hoặc A khi và chỉ khi B hay A nếu và chỉ nếu B.

Ví dụ: Cho hai mệnh đề A:"6 chia hết cho 2" và B:"4 là số chẵn"

Khi đó mệnh đề A và B đều đúng nên A ⇔ B phát biểu là "6 chia hết cho 2 khi và chỉ khi 4 là số chẵn"

7. Kí hiệu ∀, kí hiệu ∃

Cho mệnh đề chứa biến: P(x), trong đó x là biến nhận giá trị từ tập hợp X.

- Câu khẳng định: Với mọi x thuộc X thì P(x) là mệnh đề đúng và được kí hiệu là: ∀x ∈ X : P(x).

- Câu khẳng định: Có ít nhất một x ∈ X (hay tồn tại x ∈ X) để P(x) là mệnh đề đúng, kí hiệu là ∃x ∈ X : P(x).

Bài tập

Bài 1: Cho biết P ⇒ Q là mệnh đề đúng. Trong các khẳng định sau, khẳng định nào đúng?

A. P là điều kiện cần để có Q

B. là điều kiện cần để có P

C. P là điều kiện cần và đủ để có Q

D. Q là điều kiện cần và đủ để có P

Đáp án

Nếu P ⇒ Q là mệnh đề đúng thì Q là điều kiện cần để có P

Chọn đáp án B

Bài 2: Xét mệnh đề P: "∀x ∈ R, x2 + 1 > 0". Mệnh đề phủ định P_ của mệnh đề P là:

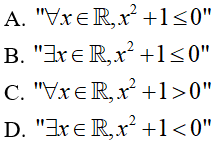
Đáp án

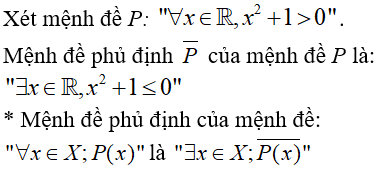
Chọn đáp án B

Bài 3: Mệnh đề phủ định của mệnh đề P: "∃x ∈ Z: x² + x + 1 là một số nguyên tố" là:

Đáp án

Mệnh đề phủ định của mệnh đề P: "∃x ∈ Z: x² + x + 1 là một số nguyên tố" là:

B. "∀x ∈ Z: x² + x + 1" không là số nguyên tố"

Chọn đáp án B

Bài 4: Mệnh đề nào sau đây có mệnh đề phủ định đúng?

Đáp án

Chọn đáp án C

Bài 5: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo sai?

A. Tứ giác là hình bình hành thì có hai cặp cạnh đối bằng nhau.

B. Tam giác đều thì có ba góc có số đo bằng 60°.

C. Hai tam giác bằng nhau thì có diện tích bằng nhau.

D. Một tứ giác có bốn góc vuông thì tứ giác đó là hình chữ nhật.

Đáp án

Ta tìm mệnh đề đảo của các mệnh đề đã cho.

Gọi A’; B’; C’ và D’ lần lượt là các mệnh đề đảo của các mệnh đề A, B, C ,D.

A’. Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành

Mệnh đề này đúng- theo dấu hiệu nhận biết hình bình hành.

B’. Tam giác có ba góc có số đo bằng 60° là tam giác đều.

Mệnh đề này đúng.

C’. Hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau.

Mệnh đề này sai. Hai tam giác có diện tích bằng nhau thì chưa chắc hai tam giác đó bằng nhau.

Ví dụ cho tam giác ABC không cân, đường cao AH. Gọi M là trung điểm BC.

Khi đó diện tích tam giác AMB và AMC là bằng nhau nhưng hai tam giác này không bằng nhau.

D’. Một tứ giác là hình chữ nhật thì tứ giác đó có bốn góc vuông.

Mệnh đề này đúng theo định nghĩa hình chữ nhật.

Chọn đáp án C

Bài 6: Trong các mệnh đề sau, mệnh đề nào sai?

A. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một cạnh bằng nhau.

B. Một tam giác là tam giác vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại.

C. Một tam giác là tam giác đều khi và chủ khi nó có hai đường trung tuyến bằng nhau và có một góc bằng 60°.

D. Một tứ giác là hình chữ nhật khi và chỉ khi nó có 3 góc vuông.

Đáp án

Mệnh đề A: Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một cạnh bằng nhau là sai.

* Hai tam giác bằng nhau thì suy ra chúng đồng dạng và có một cạnh bằng nhau.

Ngược lại, hai tam giác đồng dạng và có 1 cạnh bằng nhau thì chưa chắc hai tam giác đó bằng nhau.

Chọn đáp án A

Bài 7: Cho mệnh đề đúng: "Tất cả mọi người bạn của Nam đều biết bơi". Trong các mệnh đề sau, mệnh đề nào đúng?

A. Bình biết bơi nên Bình là bạn của Nam.

B. Chiến là bạn của Nam nên Chiến không viết bơi.

C. Minh không biết bơi nên Minh không là bạn của Nam.

D. Thành không là bạn của Nam nên Thành không biết bơi.

Đáp án

Mệnh đề C đúng: Minh không biết bơi nên Minh không là bạn của Nam.

Chọn đáp án C

Bài 8: Cho các mệnh đề sau:

(I) "21 là số nguyên tố"

(II) "Phương trình x2 + 4x - 1 = 0 có hai nghiệm thực"

(III) ""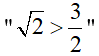

(IV) "Số dư khi chia 2006 cho 4 là 2"

(V) "Năm 2016 là năm nhuận"

Trong các mệnh đề trên, số mệnh đề đúng là:

A. 2;

B. 3;

C. 4;

D. 5.

Đáp án

Vì 21⋮3 nên 21 là một hợp số, suy ra mệnh đề (I) sai.

Phương trình x² + 4x - 1 = 0 có hai nghiệm thực là

Ta có 2006 = 501 × 4 + 2 nên 2006 chia 4 dư 2, mệnh đề (IV) đúng.

Năm 2016 là năm nhuận, có 366 ngày, tháng 2 có 29 ngày (Dấu hiệu nhận biết: Năm nhuận là năm chia hết cho 4). Mệnh đề (V) đúng.

Vậy, trong các mệnh đề trên có 3 mệnh đề đúng là các mệnh đề (II), (IV), (V).

Chọn đáp án B

Bài 9: Xét mệnh đề P:∃x ∈ R: 2x - 3 < 0 . Mệnh đề phủ định P_ của mệnh đề là:

Đáp án

Chú ý: Mệnh đề phủ định của mệnh đề "∃x ∈ X, P(x)" là "∀x ∈ X, P(x)____" .

Chọn đáp án C

Bài 10: Cho mệnh đề A: "∀x ∈ R: x ≥ 2 ⇒ x2 ≥ 4". Mệnh đề phủ định của mệnh đề A: "∀x ∈ R: x ≥ 2 ⇒ x2 ≥ 4" là:

Đáp án

Chú ý: Mệnh đề phủ định của mệnh đề "∃x ∈ X, P(x)" là "∀x ∈ X, P(x)____" .

Chọn đáp án B

Bài 11: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. "Nếu a > b thì a² > b²".

B. "Nếu tích ab của hai số nguyên a và b là một số lẻ thì a, b là các số lẻ".

C. "Nếu một tứ giác là hình thoi thì có hai đường chéo vuông góc với nhau".

D. "Nếu một số nguyên chia hết cho 6 thì nó chia hết cho 3".

Đáp án

Mệnh đề đảo A', B', C', D' của các mệnh đề trong các phương án A, B, C, D lần lượt là:

A': "Nếu a² > b² thì a > b ".

Ta có: (-1)² > 0² nhưng -1 < 0 nên A' là mệnh đề sai.

B' : "Nếu hai số nguyên a và b là các số lẻ thì tích ab là một số lẻ".

Nếu a và b là hai số nguyên lẻ thì a = 2k + 1, b = 2l + 1(k, l ∈ Z), ta có ab = (2k + 1)(2l + 1) = 4kl + 2k + 2l + 1 nên tích ab cũng là một số lẻ. Do đó mệnh đề B' đúng.

C' : "Nếu một tứ giác có hai đường chéo vuông góc với nhau thì tứ giác đó là hình thoi". C' là một mệnh đề sai.

D' : "Nếu một số nguyên chia hết cho 3 thì nó chia hết cho 6".

Ta có 9⋮3 nhưng 9 ⋮/ 6 nên D' là một mệnh đề sai.

Chú ý:

- B là mệnh đề đúng vì giả sử ít nhất một trong hai số a, b chẵn thì ta có ab là một số chẵn.

- Mệnh đề B và mệnh đề đảo B’ đều là các mệnh đề đúng nên cặp mệnh đề trong phương án B là cặp mệnh đề tương đương. Ta còn nói: "Tích ab của hai số nguyên a và b là một số lẻ khi và chỉ khi a; b là các số lẻ".

Chọn đáp án B

Bài 12: Trong các câu sau, có bao nhiêu câu là mệnh đề?

(I) Hãy mở cửa ra!

(II) Số 20 chia hết cho 8

(III) Số 17 là một số nguyên tố. (

(IV) Bạn có thích ăn phở không?

A. 1

B. 2

C. 3

D. 4

Đáp án

Có 2 câu là mệnh đề là (II), (III).

Câu (I) là câu cảm thán ; câu (IV) là câu hỏi nên không là mệnh đề.

Chọn đáp án B

Bài 13: Trong các mệnh đề sau, mệnh đề nào sai?

A. Nếu n là số nguyên lẻ thì n² là số lẻ.

B. Điều kiện cần và đủ để số tự nhiên n chia hết cho 3 là tổng các chữ số của n chia hết cho 3.

C. Tứ giác ABCD là hình chữ nhật khi và chỉ khi AC = BD .

D. Tam giác ABC là tam giác đều khi và chỉ khi AB = BC và A⌢.

Đáp án

* A. Nếu n là số nguyên lẻ thì n² là số lẻ đây là mệnh đề đúng

* B. Điều kiện cần và đủ để số tự nhiên n chia hết cho 3 là tổng các chữ số của n chia hết cho 3. Mệnh đề này đúng; đây là dấu hiệu chia hết cho 3.

* C. Tứ giác ABCD là hình chữ nhật khi và chỉ khi AC = BD là mệnh đề sai.

Nếu tứ giác ABCD là hình chữ nhật thì hai đường chéo AC và BD bằng nhau.

Ngược lại, tứ giác ABCD có 2 đường chéo bằng nhau nhưng không cắt nhau tại trung điểm mỗi đường thì không thể là hình chữ nhật

* D. Tam giác ABC là tam giác đều khi và chỉ khi AB = BC và A⌢ = 60° là mệnh đề đúng.

Chọn đáp án C

Bài 14: Mệnh đề nào đúng trong các mệnh đề sau?

Đáp án

Vì 0 = 0² nên mệnh đề A sai

Vì 2.0² + 1 = 1 nên mệnh đề B sai

Ta có 0,1 > 0, 01 nên mệnh đề C đúng.

9x² - 1 = 0 khi và chỉ khi x = -1/3 hoặc x = 1/3. Không có số nguyên x nào thỏa mãn 9x² - 1 = 0 nên mệnh đề D sai.

Chọn đáp án C

Bài 15: Mệnh đề nào sau đây đúng?

Đáp án

* Ta có: 0 ≥ -3 nhưng 0² < 9 nên mệnh đề A sai.

* ∀x ∈ R; x > 3 ⇒ x² > 9 là mệnh đề đúng

* (-4)² > 9 nhưng -4 < 3 nên mệnh đề C sai.

* (-4)² > 9 nhưng -4 < -3 nên mệnh đề D sai

Chọn đáp án B

Bài 16: Cho a, b là hai số tự nhiên. Mệnh đề nào sau đây sai?

A. Nếu a, b là hai số lẻ thì ab lẻ.

B. Nếu a chẵn và b lẻ thì ab lẻ.

C. Nếu a và b lẻ thì a + b chẵn.

D. Nếu a² lẻ thì a lẻ.

Đáp án

Mệnh đề B: Nếu a chẵn và b lẻ thì ab lẻ là mệnh đề sai.

Ví dụ: a= 2 và b = 3 nhưng a.b = 6 là số chẵn.

Chọn đáp án B

Bài 17: Cho mệnh đề chứa biến P(x): "x ∈ R: x + 8 ≤ x²". Mệnh đề đúng là:

A. P(-2)

B. P(0)

C. P(3)

D. P(5)

Đáp án

Với x = -2 ta có mệnh đề P(-2): "-2 + 8 ≤ (-2)²", là mệnh đề sai.

Với x = 0 ta có mệnh đề P(0): "0 + 8 ≤ 0²", là mệnh đề sai.

Với x = 3 ta có mệnh đề P(3): "3 + 8 ≤ 3², là mệnh đề sai.

Với x = 5 ta có mệnh đề P(5): "5 + 8 ≤ 5², là mệnh đề đúng.

Chọn đáp án D

Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 2: Tập hợp và các phép toán trên tập hợp

Bài tập cuối chương 1

Bài 3: Bất phương trình bậc nhất hai ẩn

Bài 4: Hệ bất phương trình bậc nhất hai ẩn

Bài tập cuối chương 2