Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng

Phương Thảo Ngày: 26-10-2022 Lớp 10

3.2 K

Với Giải SBT Toán 10 Tập 1 trong Bài 3: Giải tam giác và ứng dụng thực tế Sách bài tập Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10.

Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng

Bài 3 trang 79 SBT Toán 10: Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng $\hat{R Q A} = 79^{\circ}$ , người đó lùi ra xa một khoảng cách $L M = 50$ m thì nhìn thấy đỉnh tòa nhà với góc nâng $\hat{R P A} = 65^{\circ}$ . Hãy tính chiều cao của tòa nhà, biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là $P L = Q M = 1, 4$ m (hình 6)

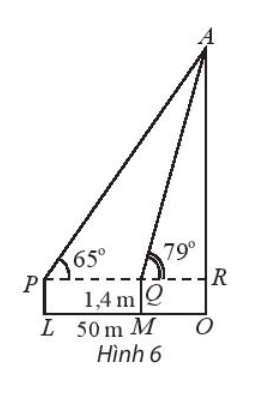
Lời giải:

Ta có chiều cao của nhà cao tầng là $A O = A R + R O = A R + 1, 4$

Góc $\hat{A Q R}$ là góc ngoài của tam giác APQ tại đỉnh Q suy ra $\hat{A Q R} = \hat{A P Q} + \hat{Q A P} \Rightarrow \hat{Q A P} = \hat{A Q R} - \hat{A P Q} = 79^{\circ} - 65^{\circ} = 14^{\circ}$

Áp dụng định lí sin vào tam giác APQ ta có:

$\frac{P Q}{\sin \hat{P A Q}} = \frac{A Q}{\sin \hat{A P Q}} = \frac{50}{\sin 14^{\circ}} \Rightarrow A Q = \frac{50}{\sin 14^{\circ}} . \sin 65^{\circ}$

Xét tam giác AQR ta có:

$\frac{A R}{\sin \hat{A Q R}} = \frac{A Q}{\sin \hat{A R Q}} = \frac{\frac{50}{\sin 14^{\circ}} . \sin 65^{\circ}}{\sin 90^{\circ}} \Rightarrow A R = \frac{\frac{50}{\sin 14^{\circ}} . \sin 65^{\circ}}{\sin 90^{\circ}} . \sin 79^{\circ} ≃ 183, 87$