Với Giải SBT Toán 10 Tập 1 trong Bài 2: Định lí côsin và định lí sin Sách bài tập Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10.
Nội dung bài viết
SBT Toán 10 Chân trời sáng tạo Bài 2: Định lí côsin và định lí sin
Bài 1 trang 74 SBT Toán 10: Tính độ dài các cạnh chưa biết trong các tam giác sau:

Lời giải:
a) Sử dụng định lí côsin ta có:
BC2=AB2+AC2−2AB.AC.cosA=102+92−2.10.9.cos65∘≃104,93⇒BC≃√104,96≃10,24
b) Ta có: ˆM+ˆN+ˆP=180∘⇒ˆP=180∘−ˆM−ˆN=180∘−34∘−112∘=34∘
Áp dụng định lí sin ta có:
MNsinP=MPsinN=NPsinM=2R⇔MNsin34∘=MPsin112∘=22sin34∘≃30,34
⇒MN=22,MP≃36,48 (cm)
Bài 2 trang 74 SBT Toán 10: Cho tam giác ABC , biết cạnh a=75 cm, ˆB=80∘,ˆC=40∘
a) Tính các góc, các cạnh còn lại của tam giác ABC
b) Tính bán kính đường tròn ngoại tiếp của tam giác ABC
Lời giải:
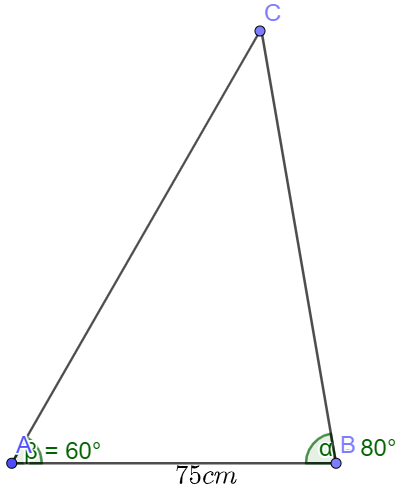
a) Ta có ˆA+ˆB+ˆC=180∘
Suy ra ˆA=180∘−(ˆB+ˆC)=180∘−(80∘+40∘)=60∘
Áp dụng định lí sin ta có:
ABsinC=BCsinA=ACsinB=2R⇔ABsin40∘=75sin60∘=ACsin80∘=50√3
⇒AB≃55,67;AC≃85,29
b) Ta có BCsinA=2R⇒R=BC2sinA=752.sin60∘=25√3
Bài 3 trang 75 SBT Toán 10: Tính góc lớn nhất của tam giác ABC, biết các cạnh là a=8,b=12,c=6
Lời giải:
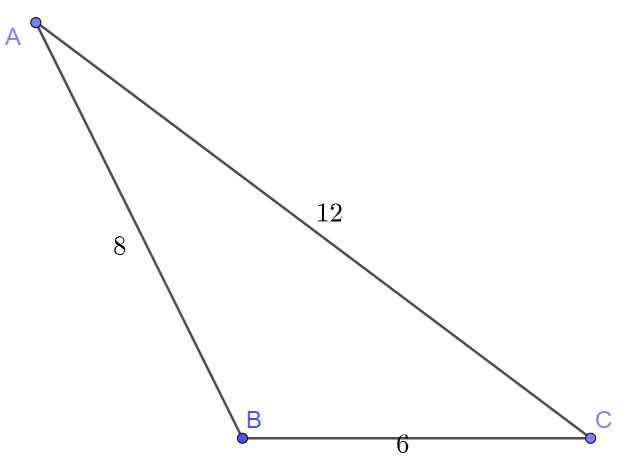
Áp dụng hệ quả của định lí côsin ta có:
cosA=b2+c2−a22bc=122+62−822.12.6=2936⇒ˆA≃36∘20′
cosB=a2+c2−b22ac=82+62−1222.8.6=−1124⇒ˆB≃117∘17′
cosC=a2+b2−c22ab=82+122−622.12.8=4348⇒ˆA≃26∘23′
Ta thấy rằng 117∘17′>36∘20′>26∘23′ nên góc B là góc lớn nhất trong tam giác ABC đã cho
Bài 4 trang 75 SBT Toán 10: Tính khoảng cách giữa hai điểm P và Q của một hồ nước (hình 7). Cho biết từ một điểm O cách hai điểm P và Q lần lượt là 1400 m và 600 m người quan sát nhìn thấy một góc 76∘
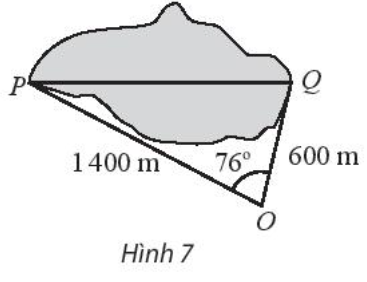
Lời giải:
Áp dụng định lí côsin ta có:
PC2=OP2+OQ2−2OP.OQ.cosO=14002+6002−2.1400.600.cos76∘=1913571,215⇒PQ=√1913571,215≃1383,32
Vậy khoảng cách giữa hai điểm P và Q của hồ nước trên gần bằng 1383,32 m
Bài 5 trang 75 SBT Toán 10: Cho tam giác ABC với BC=a;AC=b;AB=c. Chứng minh rằng:
1+cosA=(a+b+c)(−a+b+c)2bc
Lời giải:
Áp dụng định lí côsin ta có:
cosA=b2+c2−a22bc⇒cosA+1=b2+c2−a2+2bc2bc (1)
b2+c2−a2+2bc2bc=(b2+c2+2bc)−a22bc=(b+c)2−a22bc=(b+c+a)(b+c−a)2bc (2)
Từ (1) và (2) suy ra 1+cosA=(a+b+c)(−a+b+c)2bc (đpcm)
Bài 6 trang 75 SBT Toán 10: Cho tam giác ABC có a=24cm, b=26cm, c=30cm
a) Tính diện tích tam giác ABC
b) Tính bán kính đường tròn nội tiếp của tam giác ABC
Lời giải:
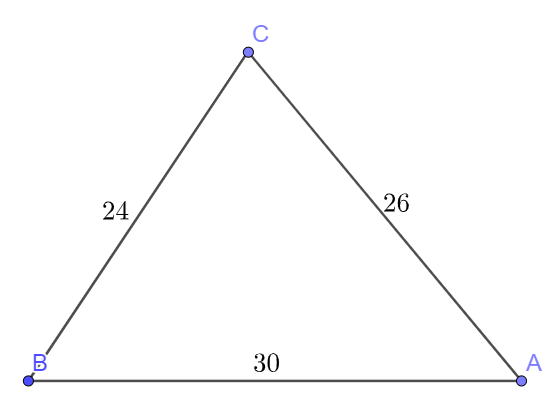
a) Ta có: p=12(24+26+30)=40 (cm)
Áp dụng công thức Heron, ta có:
S=√p(p−a)(p−b)(p−c)=√40.(40−24)(40−26)(40−30)=80√14 (cm2)
b) Ta có công thức S=pr
Suy ra r=Sp=80√1440=2√14 (cm)
Bài 7 trang 75 SBT Toán 10: Cho tam giác MNP có MN=10,MP=20 và ˆM=42∘
a) Tính diện tích tam giác MNP
b) Gọi O là tâm đường tròn ngoại tiếp tam giác MNP. Tính diện tích tam giác ONP
Lời giải:
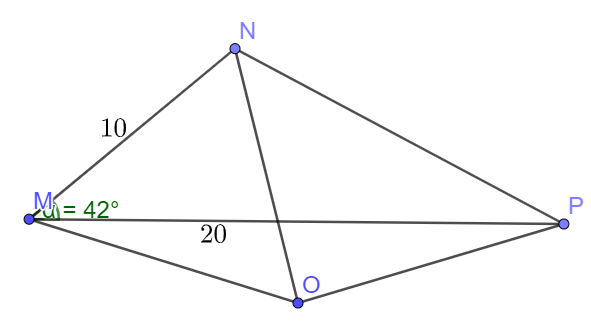
a) Ta có công thức S=12absinC=12.MN.MP.sinM
=12.10.20.sin42∘≃66,91 (đvdt)
b) O là tâm đường tròn ngoại tiếp tam giác MNP nên ta có:
OM=ON=OP=R=NP2sinM (*)
Áp dụng định lí côsin ta tính được NP như sau:
NP=√MP2+MN2−2.MP.MN.cosM≃14,24 (cm)
Thay NP vừa tính được vào (*) ta có:
OM=ON=OP=R=NP2sinM=14,242.sin42∘≃10,64
Tam giác ONP có ON=OP=10,64;NP=14,24
Áp dụng công thức Heron, ta có:
S=√p(p−a)(p−b)(p−c)≃56,3(cm2)
Lời giải:
Gọi AH, BK, CI là đường cao của tam giác ABC kẻ từ đỉnh A, B, C
GH’, GK’, GI’ là đường cao của tam giác GBC, GAC, GAB kẻ từ G xuống BC, AC, AB
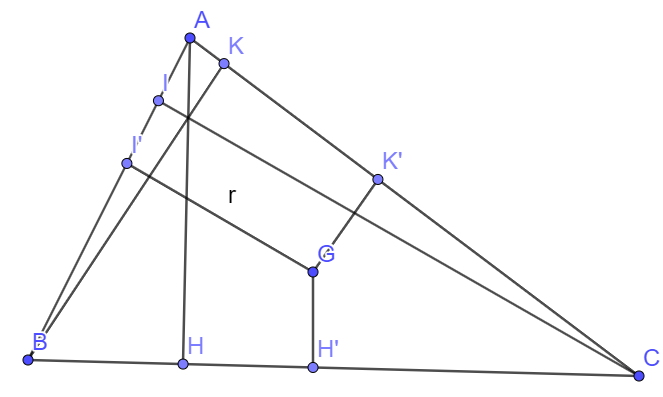
Ta có:
SGBC=12BC.GH′;SGAC=12AC.GK′;SGBA=12BA.GI′
Mà G là trọng tâm của tam giác ABC nên GH′=13AH;GK′=13BK;GI′=13CI
Suy ra SGBC=16BC.AH;SGAC=16AC.BK;SGBA=16BA.CI (1)
Mặt khác ta có SABC=12BC.AH=12AB.CI=12AC.BK (2)
Từ (1) và (2) ta có SGBC=SGAB=SGAC=13SABC (đpcm)
Bài 9 trang 75 SBT Toán 10: Cho tam giác ABC và có các điểm B’, C’ trên các cạnh AB, AC
Chứng minh SABCSAB′C′=AB.ACAB′.AC′
Lời giải:
Ta có:
SABC=12AB.AC.sinA;SAB′C′=12AB′.AC′.sinA
Suy ra SABCSAB′C′=12AB.AC.sinA12AB′.AC′.sinA=AB.ACAB′.AC′(đpcm)
Bài 10 trang 75 SBT Toán 10: Tính diện tích bề mặt của một miếng bánh mì kẹp kebab hình tam giác có hai cạnh lần lượt là 10 cm, 12 cm và góc tạo bởi hai cạnh đó là 35∘
Lời giải:
Miêu tả bề mặt của miếng bánh mì như hình dưới đây
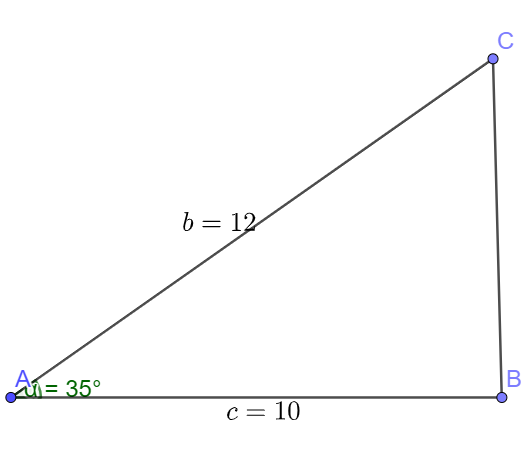
Ta có:
(cm2)
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.