Toán 10 Chân trời sáng tạo: Bài tập cuối chương 4

Hoàng Huyền Trang Ngày: 08-02-2023 Lớp 10

763

Toptailieu.vn giới thiệu Giải bài tập Toán lớp 10 Bài tập cuối chương IV sách Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10 Tập 1. Mời các bạn đón xem:

Toán 10 Chân trời sáng tạo: Bài tập cuối chương 4

Câu hỏi trang 78 Toán 10

Bài 1 trang 78 Toán 10 Tập 1: Cho tam giác ABC. Biết $a = 49, 4; b = 26, 4; \hat{C} = 47^{\circ} 20^{'} .$ Tính hai góc $\hat{A}, \hat{B}$ và cạnh c.

Phương pháp giải

Bước 1: Tính cạnh c: Áp dụng định lí cosin: $c^{2} = b^{2} + a^{2} - 2 a b \cos C$

Bước 2: Tính hai góc $\hat{A}, \hat{B}$ : Áp dụng định lí sin: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

Lời giải

Áp dụng định lí cosin trong tam giác ABC, ta có: $\begin{array}{l} c^{2} = b^{2} + a^{2} - 2 a b \cos C \\ \Leftrightarrow c^{2} = 26, 4^{2} + 49, 4^{2} - 2.26, 4.49, 4 \cos 47^{\circ} 20^{'} \\ \Rightarrow c \approx 37 \end{array}$

Áp dụng định lí sin, ta có: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

$\begin{array}{l} \Leftrightarrow \frac{49, 4}{\sin A} = \frac{26, 4}{\sin B} = \frac{37}{\sin 47^{\circ} 20^{'}} \\ \Rightarrow \sin A = \frac{49, 4. \sin 47^{\circ} 20^{'}}{37} \approx 0, 982 \Rightarrow \hat{A} \approx 79^{\circ} \\ \Rightarrow \hat{B} \approx 180^{\circ} - 79^{\circ} - 47^{\circ} 20^{'} = 53^{\circ} 40^{'} \end{array}$

Bài 2 trang 78 Toán 10 Tập 1: Cho tam giác ABC. Biết $a = 24, b = 13, c = 15.$ Tính các góc $\hat{A}, \hat{B}, \hat{C} .$

Phương pháp giải

Áp dụng hệ quả của định lí cosin:

Từ đó suy ra các góc $\hat{A}, \hat{B}, \hat{C} .$ $\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}; \cos B = \frac{a^{2} + c^{2} - b^{2}}{2 a c}; \cos C = \frac{a^{2} + b^{2} - c^{2}}{2 a b}$

Lời giải

Áp dụng hệ quả của định lí cosin, ta có:

$\begin{array}{l} \cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}; \cos B = \frac{a^{2} + c^{2} - b^{2}}{2 a c} \\ \Rightarrow \cos A = \frac{13^{2} + 15^{2} - 24^{2}}{2.13.15} = - \frac{7}{15}; \cos B = \frac{24^{2} + 15^{2} - 13^{2}}{2.24.15} = \frac{79}{90} \\ \Rightarrow \hat{A} \approx 117, 8^{\circ}, \hat{B} \approx 28, 6^{o} \\ \Rightarrow \hat{C} \approx 33, 6^{o} \end{array}$

Bài 3 trang 78 Toán 10 Tập 1: Cho tam giác ABC có $a = 8, b = 10, c = 13.$ Tính các góc $\hat{A}, \hat{B}, \hat{C} .$

Lời giải a

a) Tam giác ABC có góc tù không?

Phương pháp giải:

Áp dụng hệ quả của định lí cosin: $\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}; \cos B = \frac{a^{2} + c^{2} - b^{2}}{2 a c}; \cos C = \frac{a^{2} + b^{2} - c^{2}}{2 a b}$

Từ đó suy ra các góc $\hat{A}, \hat{B}, \hat{C} .$

Lời giải

Áp dụng hệ quả của định lí cosin, ta có:

$\begin{array}{l} \cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}; \cos B = \frac{a^{2} + c^{2} - b^{2}}{2 a c} \\ \Rightarrow {\begin{cases} \cos A = \frac{10^{2} + 13^{2} - 8^{2}}{2.10.13} = \frac{41}{52} > 0; \\ \cos B = \frac{8^{2} + 13^{2} - 10^{2}}{2.8.13} = \frac{133}{208} > 0 \\ \cos C = \frac{8^{2} + 10^{2} - 13^{2}}{2.8.13} = - \frac{1}{32} < 0 \end{cases} \end{array}$

$\Rightarrow \hat{C} \approx 91, 79^{\circ} > 90^{\circ}$ , tam giác ABC có góc C tù.

Lời giải b

b) Tính độ dài trung tuyến AM, diện tích tam giác và bán kính đường tròn ngoại tiếp tam giác đó.

Phương pháp giải:

+) Tính AM: Áp dụng định lí cosin trong tam giác ACM:

$A M^{2} = A C^{2} + C M^{2} - 2. A C . C M . \cos C$

+) Tính diện tích:

Áp dụng công thức heron: $S = \sqrt{p (p - a) (p - b) (p - c)}$

+) Tính R: Áp dụng định lí sin: $\frac{c}{\sin C} = 2 R \Rightarrow R = \frac{c}{2 \sin C}$

Lời giải

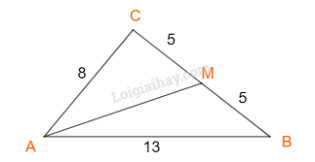
Bài 3 trang 78 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

+) Áp dụng định lí cosin trong tam giác ACM, ta có:

$\begin{array}{l} A M^{2} = A C^{2} + C M^{2} - 2. A C . C M . \cos C \\ \Leftrightarrow A M^{2} = 8^{2} + 5^{2} - 2.8.5. (- \frac{1}{32}) = 91, 5 \\ \Rightarrow A M \approx 9, 57 \end{array}$

+) Ta có: $p = \frac{8 + 10 + 13}{2} = 15, 5$ .

Áp dụng công thức heron, ta có: $S = \sqrt{p (p - a) (p - b) (p - c)} = \sqrt{15, 5. (15, 5 - 8) . (15, 5 - 10) . (15, 5 - 13)} \approx 40$

+) Áp dụng định lí sin, ta có:

$\frac{c}{\sin C} = 2 R \Rightarrow R = \frac{c}{2 \sin C} = \frac{13}{2. \sin 91, 79^{\circ}} \approx 6, 5$

Lời giải c

c) Lấy điểm D đối xứng với A qua C.

Phương pháp giải:

Áp dụng định lí cosin trong tam giác BCD:

$B D^{2} = C D^{2} + C B^{2} - 2. C D . C B . \cos \hat{B C D}$

Lời giải

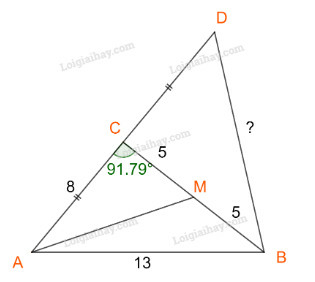
Bài 3 trang 78 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

Ta có: $\hat{B C D} = 180^{\circ} - 91, 79^{\circ} = 88, 21^{\circ}$ ; $C D = A C = 8$

Áp dụng định lí cosin trong tam giác BCD, ta có:

$\begin{array}{l} B D^{2} = C D^{2} + C B^{2} - 2. C D . C B . \cos \hat{B C D} \\ \Leftrightarrow B D^{2} = 8^{2} + 10^{2} - 2.8.10. \cos 88, 21^{\circ} \approx 159 \\ \Rightarrow B D \approx 12, 6 \end{array}$

Câu hỏi trang 79 Toán 10

Bài 4 trang 79 Toán 10 Tập 1: Cho tam giác ABC có $\hat{A} = 120^{\circ}, b = 8, c = 5.$ Tính:

Lời giải a

a) Cạnh a và các góc $\hat{B}, \hat{C} .$

Phương pháp giải:

+) Tính a: Áp dụng định lí cosin: $a^{2} = b^{2} + c^{2} - 2 b c . \cos A$

+) Tính góc $B, C$ : Áp dụng định lí sin: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

Lời giải

Áp dụng định lí cosin, ta có:

$\begin{array}{l} a^{2} = b^{2} + c^{2} - 2 b c . \cos A \\ \Leftrightarrow a^{2} = 8^{2} + 5^{2} - 2.8.5. \cos 120^{\circ} = 129 \\ \Rightarrow a = \sqrt{129} \end{array}$

Áp dụng định lí sin, ta có:

$\begin{array}{l} \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} \Rightarrow \frac{\sqrt{129}}{\sin 120^{\circ}} = \frac{8}{\sin B} = \frac{5}{\sin C} \\ \Rightarrow {\begin{cases} \sin B = \frac{8. \sin 120^{\circ}}{\sqrt{129}} \approx 0, 61 \\ \sin C = \frac{5. \sin 120^{\circ}}{\sqrt{129}} \approx 0, 38 \end{cases} \Rightarrow {\begin{cases} \hat{B} \approx 37, 59^{\circ} \\ \hat{C} \approx 22, 41^{\circ} \end{cases} \end{array}$

Lời giải b

b) Diện tích tam giác ABC

Phương pháp giải:

Áp dụng công thức $S = \frac{1}{2} b c . \sin A$

Lời giải

Diện tích tam giác ABC là: $S = \frac{1}{2} b c . \sin A = \frac{1}{2} .8 .5 . \sin 120^{\circ} = 10 \sqrt{3}$

Lời giải c

c) Bán kính đường tròn ngoại tiếp và đường cao AH của tam giác.

Phương pháp giải:

+) Áp dụng định lí sin: $R = \frac{a}{\sin A}$

+) Đường cao AH: $A H = \frac{2 S}{a}$

Lời giải

+) Theo định lí sin, ta có: $R = \frac{a}{\sin A} = \frac{\sqrt{129}}{\sin 120^{\circ}} = 2 \sqrt{43}$

+) Đường cao AH của tam giác bằng: $A H = \frac{2 S}{a} = \frac{2.10 \sqrt{3}}{\sqrt{129}} = \frac{20 \sqrt{43}}{43}$

Bài 5 trang 79 Toán 10 Tập 1: Cho hình bình hành ABCD

a) Chứng minh $2 (A B^{2} + B C^{2}) = A C^{2} + B D^{2}$

b) Cho $A B = 4, B C = 5, B D = 7.$ Tính AC.

Phương pháp giải

a) Bước 1. Tính góc AC, BD theo AB, BC, cosA dựa vào định lí cosin

Bước 2: Biến đối để suy ra đẳng thức

b) Theo câu a: $A C^{2} = 2 (A B^{2} + B C^{2}) - B D^{2}$ , từ đó suy ra AC.

Lời giải

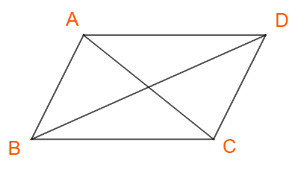
Bài 5 trang 79 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

a) Áp dụng định lí cosin ta có:

${\begin{cases} A C^{2} = A B^{2} + B C^{2} - 2. A B . B C . \cos B \\ B D^{2} = A B^{2} + A D^{2} - 2. A B . A D . \cos A \end{cases}$

Mà $A D = B C; \cos A = \cos (180^{\circ} - B) = - \cos B$

$\begin{array}{l} \Rightarrow {\begin{cases} A C^{2} = A B^{2} + B C^{2} + 2. A B . B C . \cos A \\ B D^{2} = A B^{2} + B C^{2} - 2. A B . A D . \cos A \end{cases} \\ \Rightarrow A C^{2} + B D^{2} = 2 (A B^{2} + B C^{2}) \end{array}$

b) Theo câu a, ta suy ra: $A C^{2} = 2 (A B^{2} + B C^{2}) - B D^{2}$

$\begin{array}{l} \Rightarrow A C^{2} = 2 (4^{2} + 5^{2}) - 7^{2} = 33 \\ \Rightarrow A C = \sqrt{33} \end{array}$

Bài 6 trang 79 Toán 10 Tập 1: Cho tam giác ABC có $a = 15, b = 20, c = 25.$

a) Tính diện tích tam giác ABC

b) Tính bán kính đường tròn ngoại tiếp tam giác ABC

Phương pháp giải

a) Áp dụng công thức heron: $S = \sqrt{p (p - a) (p - b) (p - c)}$ với $p = \frac{a + b + c}{2}$

b) Áp dụng công thức: $S = \frac{a b c}{4 R} \Rightarrow R = \frac{a b c}{4 S}$

Lời giải

a) Ta có: $p = \frac{a + b + c}{2} = \frac{15 + 20 + 25}{2} = 30$

Áp dụng công thức heron, ta có: $S = \sqrt{30. (30 - 15) . (30 - 20) . (30 - 25)} = 150$

b) Ta có: $S = \frac{a b c}{4 R} \Rightarrow R = \frac{a b c}{4 S} = \frac{15.20.25}{4.150} = 12, 5.$

Bài 7 trang 79 Toán 10 Tập 1: Cho tam giác ABC. Chứng minh rằng:

$\cot A + \cot B + \cot C = \frac{R (a^{2} + b^{2} + c^{2})}{a b c}$

Phương pháp giải

Tính $\cot A, \cot B, \cot C$ bằng cách: Áp dụng hệ quả của định lí sin và định lí cosin: $\sin A = \frac{a}{2 R}$ ; $\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$

Lời giải

Áp dụng hệ quả của định lí sin và định lí cosin, ta có:

$\frac{a}{\sin A} = 2 R \Rightarrow \sin A = \frac{a}{2 R}$

và $\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$

$\Rightarrow \cot A = \frac{\cos A}{\sin A} = \frac{b^{2} + c^{2} - a^{2}}{2 b c} : \frac{a}{2 R} = R . \frac{b^{2} + c^{2} - a^{2}}{a b c}$

Tương tự ta có: $\cot B = R . \frac{a^{2} + c^{2} - b^{2}}{a b c}$ và $\cot C = R . \frac{a^{2} + b^{2} - c^{2}}{a b c}$

$\begin{array}{l} \Rightarrow \cot A + \cot B + \cot C = \frac{R}{a b c} [(b^{2} + c^{2} - a^{2}) + (a^{2} + c^{2} - b^{2}) + (a^{2} + b^{2} - c^{2})] \\ = \frac{R}{a b c} (2 b^{2} + 2 c^{2} + 2 a^{2} - a^{2} - c^{2} - b^{2}) = \frac{R (a^{2} + b^{2} + c^{2})}{a b c} \end{array}$

Bài 8 trang 79 Toán 10 Tập 1: Tính khoảng cách AB giữa hai nóc tòa cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ tinh viễn thông lần lượt là 370 km, 350 km và góc nhìn từ vệ tinh đến A và B là $2, 1^{\circ} .$

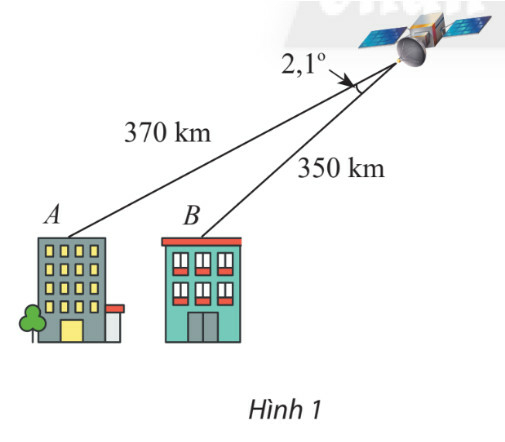
Bài 8 trang 79 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải

Áp dụng định lí cosin: $A B^{2} = 370^{2} + 350^{2} - 2.370.350. \cos 2, 1^{\circ}$

Lời giải

Áp dụng định lí cosin, ta có:

$\begin{array}{l} A B^{2} = 370^{2} + 350^{2} - 2.370.350. \cos 2, 1^{\circ} \\ \Rightarrow A B \approx 23, 96 (k m) \end{array}$

Vậy khoảng cách giữa hai tòa nhà là 23,96 km.

Bài 9 trang 79 Toán 10 Tập 1: Hai chiếc tàu thủy P và Q cách nhau 300m và thẳng hàng với chân B của tháp hải đăng AB ở trên bờ biển (Hình 2). Từ P và Q, người ta nhìn thấy tháp hải đăng AB dưới các góc và Tính chiều cao của tháp hải đăng đó.

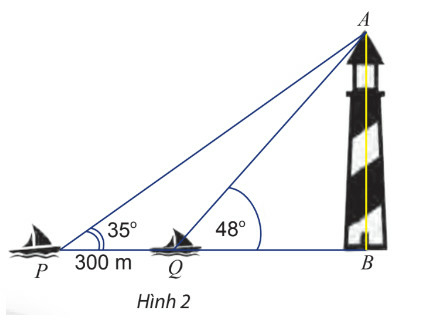
Bài 9 trang 79 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải

Bước 1: Tính AB theo QB, dựa vào tan góc P và Q.

Bước 2: Lập phương trình, tìm QB.

Bước 3: Tính AB: $A B = Q B . \tan 48^{\circ}$

Lời giải

Xét tam giác APB và AQB, ta có:

$\tan 35^{\circ} = \frac{A B}{P B} = \frac{A B}{300 + Q B}$ và $\tan 48^{\circ} = \frac{A B}{Q B}$

$\begin{array}{l} \Rightarrow A B = \tan 35^{\circ} . (300 + Q B) = \tan 48^{\circ} . Q B \\ \Leftrightarrow \tan 35^{\circ} .300 + \tan 35^{\circ} . Q B = \tan 48^{\circ} . Q B \\ \Leftrightarrow \tan 35^{\circ} .300 = (\tan 48^{\circ} - \tan 35^{\circ}) . Q B \\ \Leftrightarrow Q B = \frac{\tan 35^{\circ} .300}{\tan 48^{\circ} - \tan 35^{\circ}} \end{array}$

Mà $A B = \tan 48^{\circ} . Q B$

$\Rightarrow A B = \tan 48^{\circ} . \frac{\tan 35^{\circ} .300}{\tan 48^{\circ} - \tan 35^{\circ}} \approx 568, 5 (m)$

Vậy tháp hải đăng cao khoảng 568,5 m.

Bài 10 trang 79 Toán 10 Tập 1: Muốn đo chiều cao của một ngọn tháp, người ta lấy hai điểm A, B trên mặt đất có khoảng cách cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của hai giác kế có chiều cao là Gọi D là đỉnh tháp và hai điểm cùng thẳng hàng với thuộc chiều cao CD của tháp. Người ta do được Tính chiều cao CD của tháp.

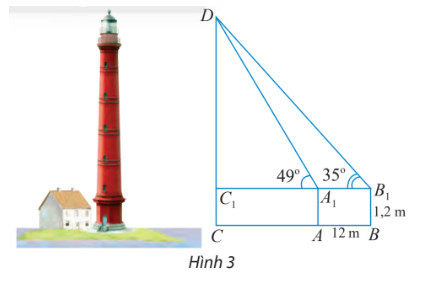
Bài 10 trang 79 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải

Bước 1: Tính góc $\hat{A_{1} D B_{1}}$ => Áp dụng định lí sin trong tam giác $A_{1} D B_{1}$ để tính $A_{1} D$

Bước 2: Tính $C_{1} D$ từ đó suy ra chiều cao của tháp.

Lời giải

Ta có: $\hat{D A_{1} C_{1}} = \hat{A_{1} D B_{1}} + \hat{D B_{1} A_{1}} \Rightarrow \hat{A_{1} D B_{1}} = 49^{\circ} - 35^{\circ} = 14^{\circ}$

Áp dụng định lí sin trong tam giác $A_{1} D B_{1}$ , ta có:

$\begin{array}{l} \frac{A_{1} D}{\sin B_{1}} = \frac{A_{1} B_{1}}{\sin D} \Leftrightarrow \frac{A_{1} D}{\sin 35^{\circ}} = \frac{12}{\sin 14^{\circ}} \\ \Rightarrow A_{1} D = \sin 35^{\circ} . \frac{12}{\sin 14^{\circ}} \approx 28, 45 \end{array}$

Áp dụng định lí sin trong tam giác $A_{1} D C_{1}$ , ta có:

$\begin{array}{l} \frac{A_{1} D}{\sin C_{1}} = \frac{C_{1} D}{\sin A_{1}} \Leftrightarrow \frac{28, 45}{\sin 90^{\circ}} = \frac{C_{1} D}{\sin 49^{\circ}} \\ \Rightarrow C_{1} D = \sin 49^{\circ} . \frac{28, 45}{\sin 90^{\circ}} \approx 21, 47 \end{array}$