Bằng cách tô màu trên lưới ô vuông như hình dưới đây, một học sinh phát hiện ra công thức sau

Phạm Thị Huyền Trang Ngày: 12-12-2022 Lớp 10

706

Với giải Khám phá 1 trang 27 Chuyên đề Toán 10 Chân trời sáng tạo chi tiết trong Bài 3: Phương pháp quy nạp toán học giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Chuyên đề Toán 10. Mời các bạn đón xem:

Giải bài tập Chuyên đề Toán lớp 10 Bài 3: Phương pháp quy nạp toán học

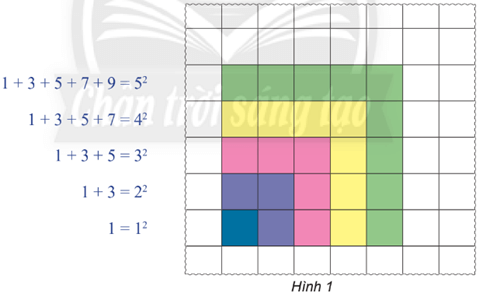
Khám phá 1 trang 27 Chuyên đề Toán 10: Bằng cách tô màu trên lưới ô vuông như hình dưới đây, một học sinh phát hiện ra công thức sau:

(ảnh 1)

1 + 3 + 5 + 7 +... + (2n – 1) = n2. (1)

a) Hãy chỉ ra công thức (1) đúng với n = 1, 2, 3, 4, 5.

b) Từ việc tô màu trên lưới ô vuông như Hình 1, bạn học sinh khẳng định rằng công thức (1) chắc chắn đúng với mọi số tự nhiên n ≥ 1. Khẳng định như vậy đã thuyết phục chưa? Tại sao?

Lời giải:

a) Với n = 1, ta có 2.1 – 1 = 1 = 12, do đó công thức (1) đúng với n = 1.

Với n = 2, ta có 1 + (2.2 – 1) = 4 = 22, do đó công thức (1) đúng với n = 2.

Với n = 3, ta có 1 + 3 + (2.3 – 1) = 9 = 32, do đó công thức (1) đúng với n = 3.

Với n = 4, ta có 1 + 3 + 5 + (2.4 – 1) = 16 = 42, do đó công thức (1) đúng với n = 4.

Với n = 5, ta có 1 + 3 + 5 + 7 + (2.5 – 1) = 25 = 52, do đó công thức (1) đúng với n = 5.

b) Mỗi lần tô thêm một hàng và cột những ô vuông, bạn học sinh đã kiểm nghiệm công thức (1) thêm một trường hợp của n. Tuy nhiên, bới tập hợp ℕ* là vô hạn nên cách làm đó không thể chứng tỏ công thức (1) đúng với mọi n ∈ ℕ*.

Xem thêm các bài giải Chuyên đề Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Khởi động trang 27 Chuyên đề Toán 10: Trong một trò chơi domino, các quân domino được xếp theo thứ tự từ quân đầu tiên đến quân cuối cùng. Biết rằng xảy ra hai điều sau:

Thực hành 1 trang 29 Chuyên đề Toán 10: Chứng minh rằng đẳng thức sau đúng với mọi

Thực hành 2 trang 29 Chuyên đề Toán 10: Chứng minh rằng bất đẳng thức sau đúng với mọi số tự nhiên n ≥ 3: 2n + 1 > n2 + n + 2

Thực hành 3 trang 31 Chuyên đề Toán 10: Chứng minh rằng n³ + 2n chia hết cho 3 với mọi n∈N^∗

Thực hành 4 trang 31 Chuyên đề Toán 10: Chứng minh rằng đẳng thức sau đúng với mọi

Thực hành 5 trang 31 Chuyên đề Toán 10: Chứng minh rằng trong mặt phẳng, n đường thẳng khác nhau cùng đi qua một điểm chia mặt phẳng thành 2n phần.

Vận dụng trang 31 Chuyên đề Toán 10: (Công thức lãi kép) Một khoản tiền A đồng (gọi là vốn) được gửi tiết kiệm có kì hạn ở một ngân hàng theo thể thức lãi kép (tiền lãi sau mỗi kì hạn nếu không rút ra thì được cộng vào vốn của kì kế tiếp).

Bài 1 trang 32 Chuyên đề Toán 10: Chứng minh các đẳng thức sau đúng với mọi

Bài 2 trang 32 Chuyên đề Toán 10: Chứng minh rằng, với mọi , ta có:

Bài 3 trang 32 Chuyên đề Toán 10: Chứng minh rằng nếu x > –1 thì (1 + x)n ≥ 1 + nx với mọi n∈N∗

Bài 4 trang 32 Chuyên đề Toán 10: Cho a, b ≥ 0. Chứng minh rằng bất đẳng thức sau đúng với mọi