Tại vòng chung kết của một trò chơi trên truyền hình, có 100 khán giả

Hoàng Huyền Trang Ngày: 03-02-2023 Lớp 10

1.2 K

Với giải Vận dụng trang 23 Toán 10 Tập 1 Chân trời sáng tạo chi tiết trong Bài 3. Các phép toán trên tập hợp giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Tại vòng chung kết của một trò chơi trên truyền hình, có 100 khán giả

Vận dụng trang 23 Toán 10 Tập 1: Tại vòng chung kết của một trò chơi trên truyền hình, có 100 khán giả tại trường quay có quyền bình chọn cho hai thí sinh A và B. Biết rằng có 85 khán giả bình chọn cho thí sinh A, 72 khán giả bình chọn cho thí sinh B và 60 khán giả bình chọn cho cả hai thí sinh. Có bao nhiêu khán giả đã tham gia bình chọn? Có bao nhiêu khán giả không tham gia bình chọn?

Phương pháp giải:

Kí hiệu A, B lần lượt là tập hợp các khán giả bình chọn cho thí sinh A và thí sinh B.

Sử dụng biểu đồ Ven, minh họa tập hợp các khán giả đã tham gia bình chọn ( $A \cup B$ ) và các khán giả không tham gia bình chọn.

Lời giải

Gọi A, B lần lượt là tập hợp các khán giả bình chọn cho thí sinh A và thí sinh B.

Theo giả thiết, $n (A) = 85, n (B) = 72, n (A \cap B) = 60$

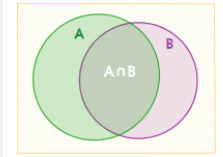
Vận dụng trang 23 SGK Toán 10 Tập 1 | Chân trời sáng tạo (ảnh 1)

Nhận thấy rằng, nếu tính tổng $n (A) + n (B)$ thì ta được số khán giả đã tham gia bình chọn, nhưng số khán giả bình chọn cho cả hai thí sinh được tính hai lần. Do đó, số khán giả đã tham gia bình chọn là:

$n (A \cup B) = n (A) + n (B) - n (A \cap B) = 85 + 72 - 60 = 97$

Như vậy trong hội trường 100 khán giả, có 97 khán giải đã tham gia bình chọn, còn lại số khán giả không tham gia bình chọn là: $100 - 97 = 3$ (khán giả).

Xem thêm các bài giải Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Hoạt động Khởi động trang 21 Toán 10 Tập 1: Có 2 đường tròn chia một hình chữ nhật thành các miền như hình bên. Hãy đặt mooix thẻ số sau đây vào miền thích hợp trên hình chữ nhật và giải thích cách làm...

Hoạt động Khám phá 1 trang 22 Toán 10 Tập 1: Bảng sau đây cho biết kết quả vòng phỏng vấn tuyển dụng vào một công ty (dấu “+” là đạt, dấu “-” là không đạt)...

Thực hành 1 trang 23 Toán 10 Tập 1: Xác định các tập hợp và , biết...

Hoạt động Khám phá 2 trang 23 Toán 10 Tập 1: Trở lại bảng thông tin về kết quả phỏng vấn tuyển dụng ở Hoạt động khám phá 1...

Thực hành 3 trang 24 Toán 10 Tập 1: Cho tập hợp...

Thực hành 4 trang 25 Toán 10 Tập 1: Xác định các tập hợp sau đây...

Bài 1 trang 25 Toán 10 Tập 1: Xác định các tập hợp và với...

Bài 2 trang 25 Toán 10 Tập 1: Xác định các tập hợp trong mỗi trường hợp sau...

Bài 3 trang 25 Toán 10 Tập 1: Cho là bội của 3 là ước của 6...

Bài 4 trang 25 Toán 10 Tập 1: Cho A và B là hai tập hợp bất kì. Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Hãy giải thích bằng cách sử dụng biểu đồ Ven...

Bài 5 trang 25 Toán 10 Tập 1: Trong số 35 học sinh của lớp 10H, có 20 học sinh thích môn Toán, 16 học sinh thích môn Tiếng Anh và 12 học sinh thích cả hai môn này. Hỏi lớp 10H...